Uniform Distribution

5.2. Uniform Distribution#

5.2.1. Understanding Uniform Distribution#

The Uniform Distribution is a type of continuous probability distribution characterized by a constant probability density function (PDF). For a continuous random variable \(X\), the PDF is represented by \(f(X)\) and is defined within the interval \([a, b]\) as:

(5.8)#\[\begin{equation} f(X) = \dfrac{1}{b - a} \quad \text{for} \quad a \leq X \leq b \end{equation}\]

Here, \(a\) and \(b\) are the lower and upper bounds, respectively, which define the range of possible values that \(X\) can assume. The key points to note are:

  • The value of \(\dfrac{1}{b - a}\) is always a constant, reflecting the uniform nature of the distribution.

  • The notation \(X \sim U(a, b)\) denotes that the random variable \(X\) follows a Uniform Distribution with the lowest value \(a\) and the highest value \(b\).

To calculate the probability that \(X\) falls within a specific interval \([c, d]\), where \(a \leq c < d \leq b\), we use the formula:

(5.9)#\[\begin{equation} P(c \leq X \leq d) = f(x) \cdot (d - c) = \dfrac{1}{b - a} \cdot (d - c) \end{equation}\]

Fig. 5.6 illustrates the concept of a Uniform Distribution, which is characterized by a constant probability density function (PDF) over a specified interval \([a, b]\). The graph shows a horizontal line segment representing the PDF, which is constant at a height of \(\dfrac{1}{b-a}\) between the points \(a\) and \(b\) on the x-axis. This indicates that every value within this interval is equally likely. The shaded area between \(c\) and \(d\) represents the probability \(P(c \leq X \leq d)\), calculated as \(\dfrac{1}{b-a} \cdot (d - c)\). This visual representation helps in understanding how the uniform distribution assigns equal probability to all values within its range and how probabilities for specific intervals are determined by the area under the PDF.

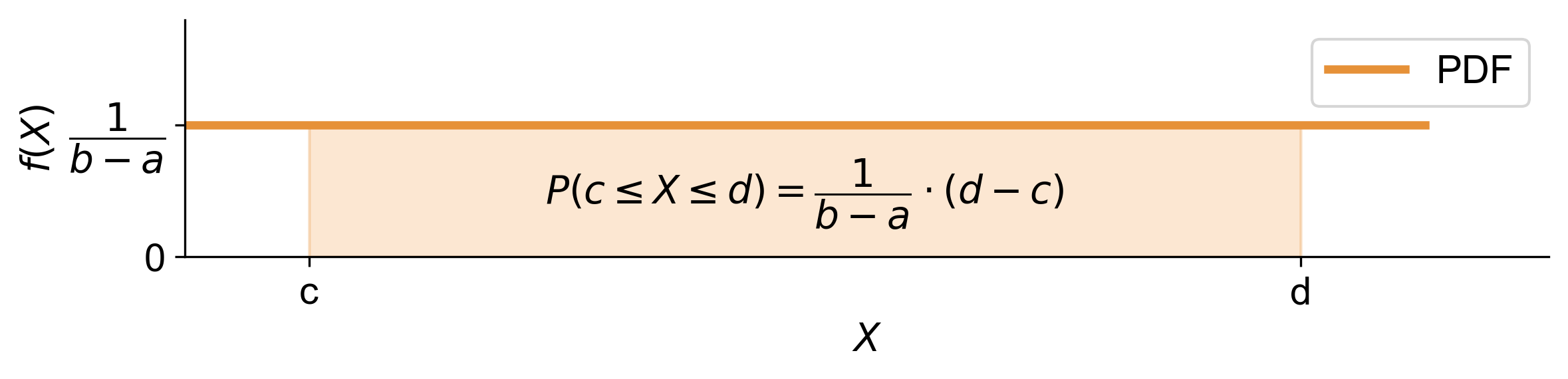
../_images/uniform_distribution_figure1.png

Fig. 5.6 Graphical representation of the constant probability density function of a uniform distribution between two bounds \(a\) and \(b\), with an example shaded area representing the probability of falling within an interval \([c,~d]\).#

Example 5.1

Given a uniform distribution with a probability density function (PDF) \(f(x) = \frac{1}{20}\) for \(0 \leq x \leq 20\), how do you calculate the probability that a random variable \(X\) falls within a range \([a, b]\)?

Solution:

The probability is found by calculating the area under the curve of \(f(x)\) between \(a\) and \(b\). Since the PDF is uniform, the graph is a horizontal line, and the area is a rectangle with width \(b - a\) and height \(\dfrac{1}{20}\).

Example 5.2

In Example 5.1

  • a. Determine the probability that \(X\) is between 0 and 4 in the given uniform distribution?

  • b. What is the probability that \(X\) is between 4 and 15?

  • c. What is the probability of a specific value, such as \(P(X = 15)\), in this continuous distribution?

Solution:

a. The probability that \(X\) is between 0 and 4 is calculated by the area under the PDF between these points:

\[\begin{align*} P(0 < X < 4) = (4 - 0) \times \frac{1}{20} = \frac{4}{20} = \frac{1}{5} = 0.2 \end{align*}\]
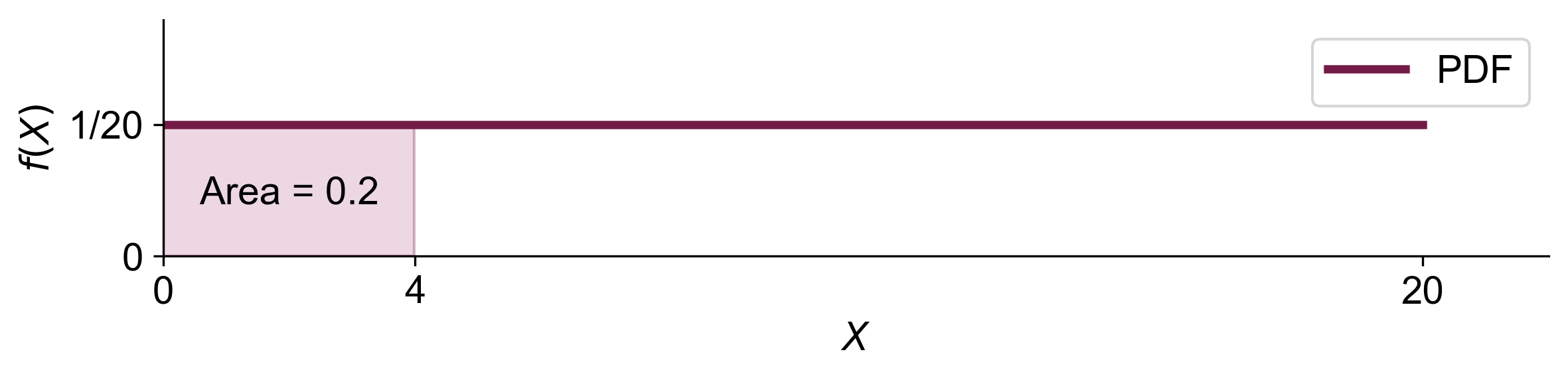
../_images/uniform_distribution_example1_2a.png

Fig. 5.7 Graphical representation of the probability that \(X\) is between 0 and 4, shown as the shaded area under the PDF.#

b. To find the probability that \(X\) is between 4 and 15, we calculate the area under the PDF from 4 to 15:

\[\begin{align*} P(4 < X < 15) = (15 - 4) \times \frac{1}{20} = \frac{11}{20} = 0.55 \end{align*}\]
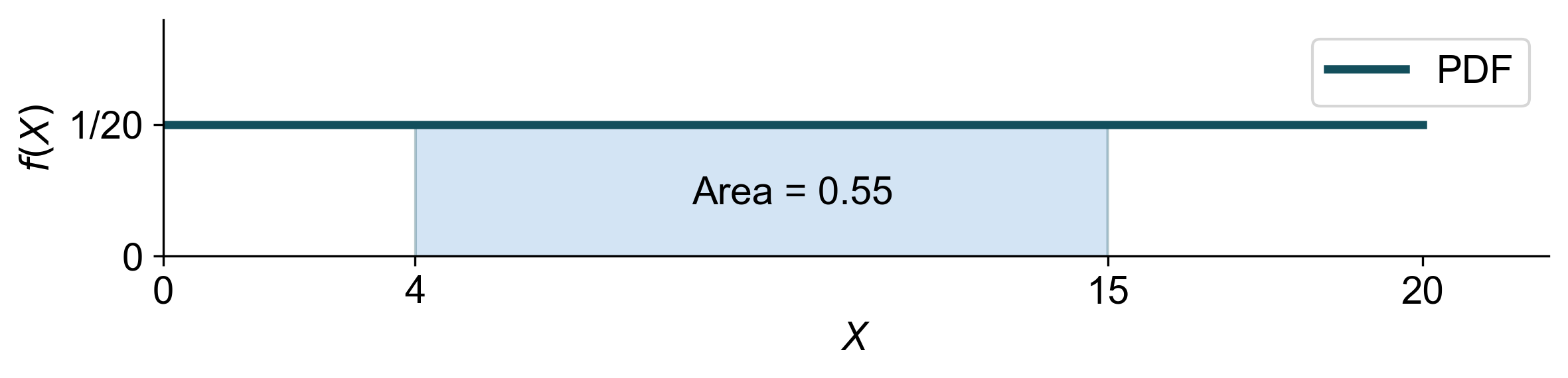
../_images/uniform_distribution_example1_2b.png

Fig. 5.8 Graphical representation of the probability that \(X\) is between 4 and 15, shown as the shaded area under the PDF.#

c. In a continuous distribution, the probability of a specific value is zero because the area under a single point, which has no width, is zero. Thus:

\[\begin{equation*} P(X = 15) = 0 \end{equation*}\]

This is a fundamental property of continuous probability distributions.

5.2.2. Mean and Standard Deviation of the Uniform Distribution#

For the Uniform Distribution, the theoretical mean (\(\mu\)) and standard deviation (\(\sigma\)) are key statistical measures that describe the distribution’s central tendency and variability, respectively. These are calculated using the following formulas:

  • Mean (\(\mu\)): The mean represents the expected average value of the distribution. For a uniform distribution defined over the interval \([a, b]\), the mean is given by:

    (5.10)#\[\begin{equation} \mu = \dfrac{a + b}{2} \end{equation}\]

    This formula indicates that the mean is simply the midpoint of the interval \([a, b]\), reflecting the uniform nature of the distribution where all values are equally likely.

  • Standard Deviation (\(\sigma\)): The standard deviation measures the spread or dispersion of the distribution. For a uniform distribution, it is calculated as:

    (5.11)#\[\begin{equation} \sigma = \sqrt{\dfrac{(b - a)^2}{12}} \end{equation}\]

    This formula shows that the standard deviation depends on the length of the interval \([a, b]\). The larger the interval, the greater the spread of the distribution. The division by 12 normalizes this spread, providing a consistent measure of variability.

Example 5.3

The data below represent the number of books sold by a bookstore in 30 different weeks. The sample mean is 8.2 and the sample standard deviation is 3.87. The data are uniformly distributed between and including the minimum value of 0 and the maximum value of 16.

  • a) Determine the values of \(a\) and \(b\).

  • b) Write the distribution in proper notation.

  • c) Calculate the theoretical mean and standard deviation.

2, 15, 5, 9, 5, 16, 10, 8, 10, 5, 12, 3, 5, 7, 4, 9, 0, 15, 7, 8, 9, 6, 12, 5, 9, 16, 15, 10, 7, 9

Solution:

a) Given the uniform distribution and the range of data:

  • \(a = 0\) (the minimum value)

  • \(b = 16\) (the maximum value)

b) The distribution in proper notation is:

\[\begin{equation*}X \sim U(0, 16)\end{equation*}\]

c) To calculate the theoretical mean (\(\mu\)) and standard deviation (\(\sigma\)) for a uniform distribution, we use the formulas:

\[\begin{align*} \mu &= \frac{a + b}{2} \\ \sigma &= \sqrt{\frac{(b - a)^2}{12}} \end{align*}\]

Substituting the values of \(a\) and \(b\):

\[\begin{align*} \mu &= \frac{0 + 16}{2} = 8 \\ \sigma &= \sqrt{\frac{(16 - 0)^2}{12}} = \sqrt{\frac{256}{12}} = \sqrt{21.33} \approx 4.62 \end{align*}\]

Therefore, the theoretical mean is 8 and the theoretical standard deviation is approximately 4.62.

Note

The theoretical mean (8) is close to the sample mean (8.23), while the theoretical standard deviation (4.62) differs somewhat from the sample standard deviation (4.30). This difference could be due to sampling variability or the data not being perfectly uniformly distributed in practice.

Example 5.4

Suppose a random variable \(Y\) follows a uniform distribution, denoted as \(Y \sim U(0, 15)\).

  • a. What is \(P(3 < Y < 12)\)?

  • b. Find the 90th percentile of \(Y\).

Solution:

a. To find \(P(3 < Y < 12)\), we calculate the area under the probability density function (PDF) between \(Y = 3\) and \(Y = 12\) for the uniform distribution \(U(0, 15)\). The PDF for \(Y\) is constant and equal to \(\frac{1}{15 - 0} = \frac{1}{15}\).

The probability, represented by the area under the curve, is calculated as the base of the rectangle (\(12 - 3\)) times the height (\(\frac{1}{15}\)):

\[\begin{align*} P(3 < Y < 12) &= (12 - 3) \times \frac{1}{15} \\ &= 9 \times \frac{1}{15} = 0.6 \end{align*}\]

Thus, \(P(3 < Y < 12) = 0.6\).

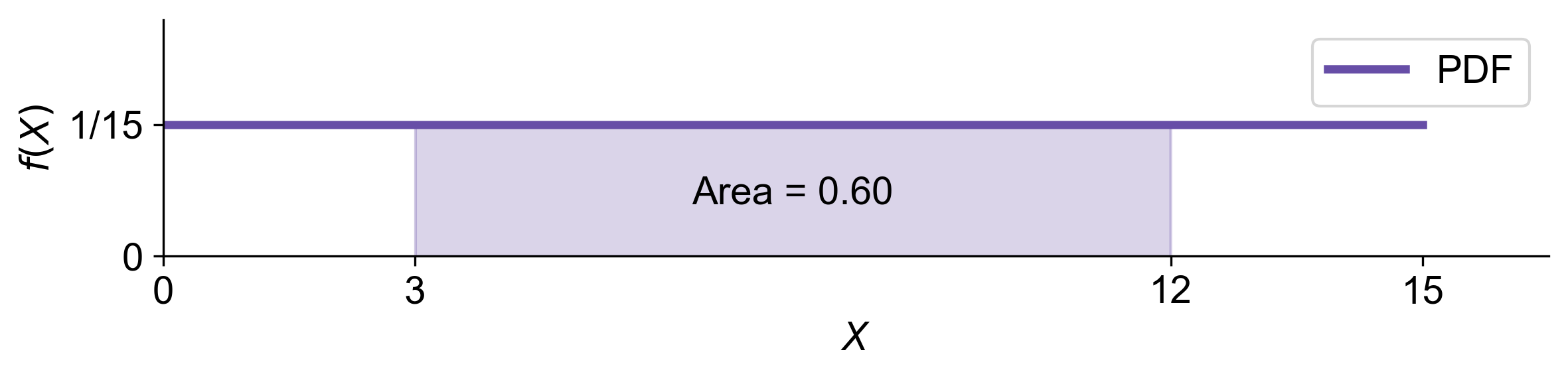
../_images/uniform_distribution_example1_4a.png

Fig. 5.9 Graphical representation of the probability that \(X\) is between 3 and 12, shown as the shaded area under the PDF.#

b. The 90th percentile of a uniform distribution \(U(a, b)\) is found by calculating \(a + 0.9 \times (b - a)\). For \(Y \sim U(0, 15)\), this is:

\[\begin{align*} 90\text{th Percentile} &= 0 + 0.9 \times (15 - 0) \\ &= 0.9 \times 15 = 13.5 \end{align*}\]

Therefore, the 90th percentile of \(Y\) is 13.5.

Example 5.5

Imagine a random variable \(Z\) that follows a uniform distribution, denoted as \(Z \sim U(0, 10)\).

  • a. What is \(P(1 < Z < 7)\)?

  • b. Find the 75th percentile of \(Z\).

Solution:

a. To find \(P(1 < Z < 7)\), we calculate the area under the probability density function (PDF) between \(Z = 1\) and \(Z = 7\) for the uniform distribution \(U(0, 10)\).

The PDF for \(Z\) is constant and equal to \(\frac{1}{10 - 0} = \frac{1}{10}\).

The probability is represented by the area of a rectangle:

\[\begin{align*} P(1 < Z < 7) &= (7 - 1) \times \frac{1}{10} \\ &= 6 \times \frac{1}{10} = 0.6 \end{align*}\]

Therefore, \(P(1 < Z < 7) = 0.6\).

../_images/uniform_distribution_example1_5a.png

Fig. 5.10 Graphical representation of the probability that \(X\) is between 1 and 7, shown as the shaded area under the PDF.#

b. The 75th percentile of a uniform distribution \(U(a, b)\) is calculated as \(a + 0.75 \times (b - a)\).

For \(Z \sim U(0, 10)\):

\[\begin{align*} 75\text{th percentile} &= 0 + 0.75 \times (10 - 0) \\ &= 0.75 \times 10 = 7.5 \end{align*}\]

Therefore, the 75th percentile of \(Z\) is 7.5.

Example 5.6

Consider a random variable \(W\) that is uniformly distributed between 5 and 25, denoted as \(W \sim U(5, 25)\).

  • a. What is the probability that \(W\) is between 10 and 20?

  • b. Find the 50th percentile of \(W\).

Solution:

a. The probability density function (PDF) for \(W\) is constant and equal to \(\frac{1}{25 - 5} = \frac{1}{20}\). To find \(P(10 < W < 20)\), we calculate the area under the PDF between \(W = 10\) and \(W = 20\):

\[\begin{align*} P(10 < W < 20) &= (20 - 10) \times \frac{1}{20} \\ &= 10 \times \frac{1}{20} = 0.5 \end{align*}\]

Thus, \(P(10 < W < 20) = 0.5\).

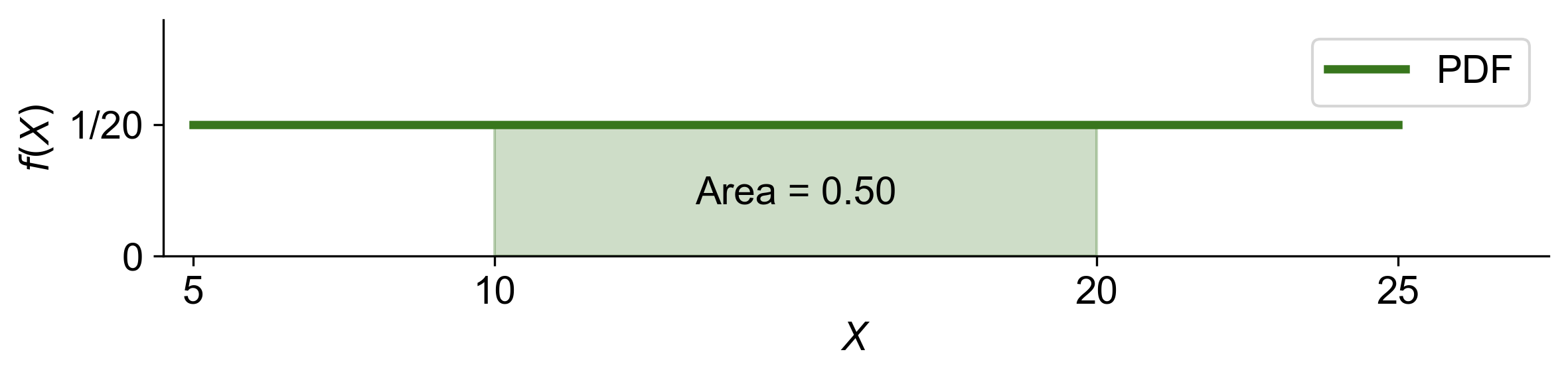
../_images/uniform_distribution_example1_6a.png

Fig. 5.11 Graphical representation of the probability that \(W\) is between 10 and 20, shown as the shaded area under the PDF.#

b. The 50th percentile, also known as the median, for a uniform distribution \(U(a, b)\) is calculated as \(\frac{a + b}{2}\). For \( W \sim U(5, 25) \), this is:

\[\begin{align*} 50\text{th Percentile} &= \frac{5 + 25}{2} = 15 \end{align*}\]

Therefore, the 50th percentile of \(W\) is 15.

Example 5.7

Consider a random variable \(V\) that follows a uniform distribution, denoted as \(V \sim U(2, 18)\).

a. Calculate \(P(4 < V < 16)\). b. Find the 30th percentile of \(V\).

Solution:

a. To find \(P(4 < V < 16)\), we calculate the area under the probability density function (PDF) between \(V = 4\) and \(V = 16\).

The PDF for \(V\) is constant and equal to \(\frac{1}{18 - 2} = \frac{1}{16}\).

\[\begin{align*} P(4 < V < 16) &= (16 - 4) \times \frac{1}{16} \\ &= 12 \times \frac{1}{16} = \frac{3}{4} = 0.75 \end{align*}\]

Therefore, \(P(4 < V < 16) = 0.75\).

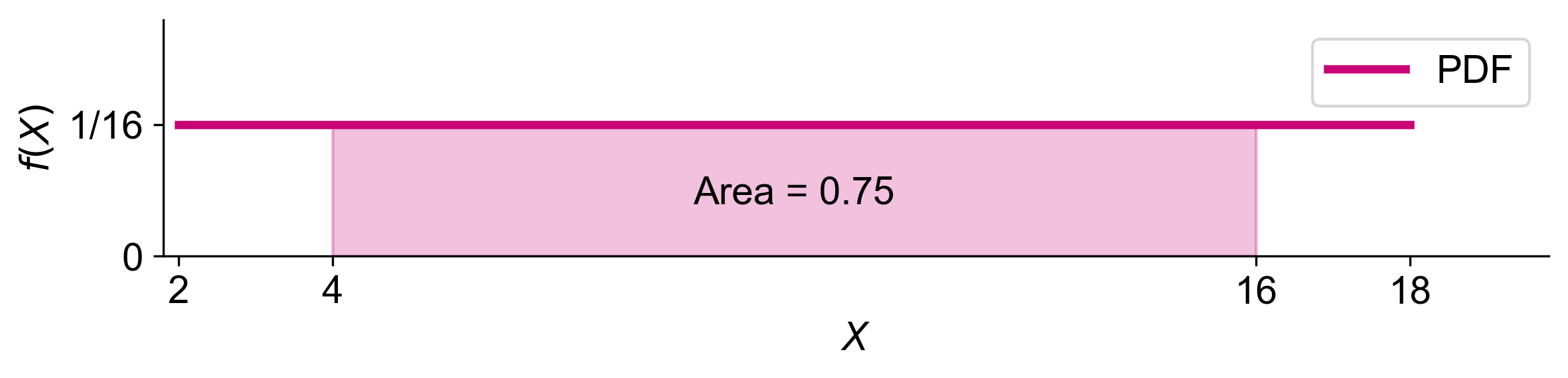
../_images/uniform_distribution_example1_7a.png

Fig. 5.12 Graphical representation of \(P(4 < V < 16)\), shown as the shaded area under the PDF.#

b. The 30th percentile for a uniform distribution \(U(a, b)\) is calculated as \(a + 0.3 \times (b - a)\).

For \(V \sim U(2, 18)\):

\[\begin{align*} 30\text{th percentile} &= 2 + 0.3 \times (18 - 2) \\ &= 2 + 0.3 \times 16 \\ &= 2 + 4.8 = 6.8 \end{align*}\]

Therefore, the 30th percentile of \(V\) is 6.8.