3.4. The Role of Complements and Equally Likely Outcomes in Probability

3.4.1. Understanding the Complement of an Event

The complement of an event A, denoted as \(A^c\), \(A'\), or \(\bar{A}\), includes all possible outcomes in the sample space S that do not result in event A.

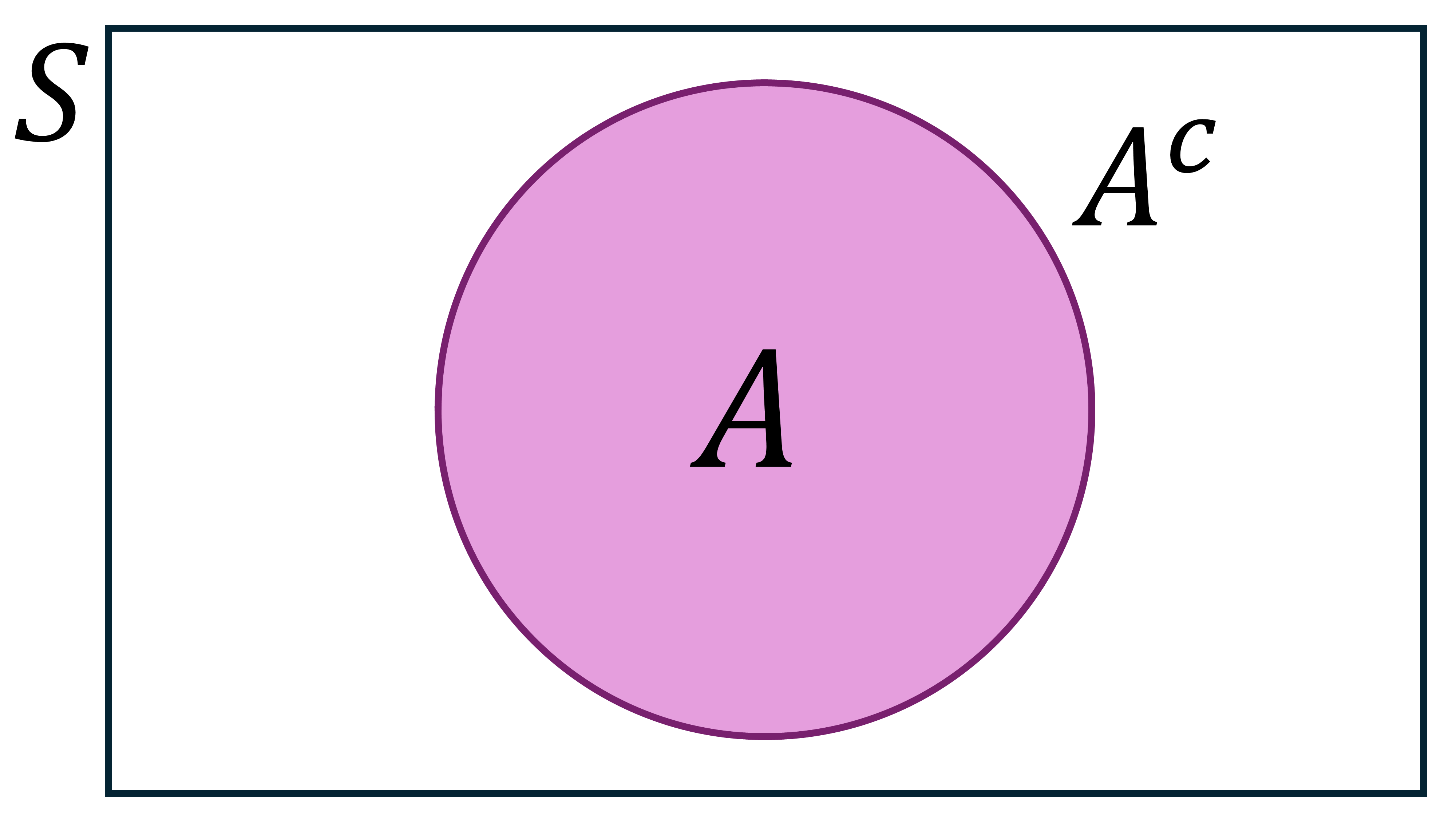
Fig. 3.43 A universal set \(S\) containing a subset \(A\) (the circle). The area outside the circle but within the rectangle represents the complement of \(A\) within \(S\) (\(A^c\)).

The Complementation Rule states that the probability of an event E occurring is equal to one minus the probability of its complement. This is represented mathematically as:

(3.7)\[\begin{equation}P(E^C) = 1 - P(E)\end{equation}\]

where \(P(E)\) is the probability of event \(E\), and \(P(E^c)\) is the probability that event \(E\) does not occur.

In essence, the complement rule helps us understand that the total probability of all outcomes in a sample space is always 1, and the probability of an event and its complement together make up this whole.

Example 3.18

Consider an experiment where a single card is drawn from a standard deck of 52 playing cards. Let \(A\) be the event that the card drawn is a heart.

• a. Define the complement of event \(A\).

• b. Calculate the probability of the complement of \(A\).

Solution:

a. The complement of the event \(A\), denoted as \(A^c\), is the event that the card drawn is not a heart.

b. The probability of drawing a heart \(P(A)\) is:

\[\begin{equation*}P(A) = \dfrac{13}{52} = \dfrac{1}{4}\end{equation*}\]

The probability of the complement of \(A\) is:

\[\begin{equation*}P(A^c) = 1 - P(A)\end{equation*}\]

Substituting the probability of \(A\):

\[\begin{equation*}P(A^c) = 1 - \dfrac{1}{4} = \dfrac{3}{4}\end{equation*}\]

Example 3.19

Consider a scenario where a six-sided die is rolled once. Let \(B\) be the event that the die shows a number less than 5.

• a. Define the complement of event \(B\).

• b. Calculate the probability of the complement of \(B\).

Solution:

a. The complement of the event \(B\), denoted as \(B^c\), is the event that the die shows a number 5 or greater.

b. The probability of rolling a number less than 5, \(P(B)\), is:

\[\begin{equation*}P(B) = \dfrac{4}{6} = \dfrac{2}{3}\end{equation*}\]

The probability of the complement of \(B\) is:

\[\begin{equation*}P(B^c) = 1 - P(B)\end{equation*}\]

Substituting the probability of \(B\):

\[\begin{equation*}P(B^c) = 1 - \dfrac{2}{3} = \dfrac{1}{3}\end{equation*}\]

3.4.2. Equally Likely Outcomes in Probability

The term “equally likely” describes scenarios where all possible outcomes of an experiment have the same chance of occurring. This uniformity means that no single outcome is favored over another.

Examples:

1. Rolling a Fair Die: A fair six-sided die has six faces, numbered 1 through 6. Each face is equally likely to land face up, giving a probability of \( \dfrac{1}{6} \) or approximately 16.67% for each number.

2. Flipping a Fair Coin: A coin has two sides: heads (H) and tails (T). A fair coin flip results in a 50% chance, or \( \dfrac{1}{2} \), for either outcome.

3. Answering a True/False Question: For a true/false question, there are two possible answers. If you guess without knowledge, there’s a 50% chance of being correct, represented by \( \dfrac{1}{2} \).

Note

“Equally likely” implies that in the long run, after many repetitions of the experiment, the frequency of each outcome will converge to these equal probabilities, even if short-term results may vary. This concept is a cornerstone of probability theory and is crucial for predicting the behavior of random processes.

Example 3.20

Imagine a fair game where a wheel is divided into equal sections of four colors:

• B for blue

• R for red

• G for green

• Y for yellow

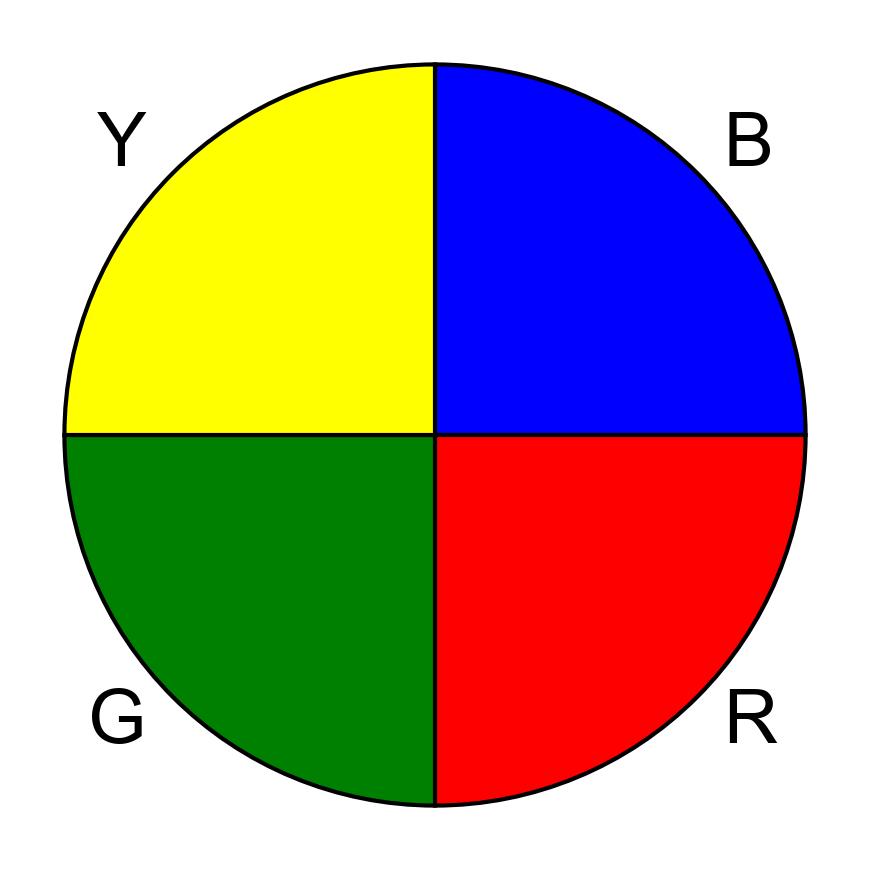
Fig. 3.44 A fair game color wheel, divided into four equal sections, each representing a different color: blue (B), red (R), green (G), and yellow (Y). Each section occupies 25% of the wheel, indicating an equal probability of landing on any given color. This setup ensures that the game is fair, with no color having a higher chance of being selected than the others.

Each section is equal in size, and there are no other colors on the wheel.

• a. If landing on Y (yellow) wins the grand prize, what is the probability \(P(Y)\) of that happening?

• b. If landing on R (red) means no prize is won, what is the probability \(P(R)\) of that happening?

Solution:

a. Since the sections are equal in size and there are four colors, the probability of landing on any specific color is:

\[\begin{equation*}P(Y) = \dfrac{1}{4}\end{equation*}\]

b. Similarly, the probability of landing on red is also:

\[\begin{equation*}P(R) = \dfrac{1}{4}\end{equation*}\]

Example 3.21

Imagine you have a box containing 150 vintage coins from around the world. The box contains 22 coins from the United States, 38 from Canada, 20 from Mexico, 28 from Spain, 26 from France, and the rest are from Italy. One coin is selected at random from the box.

Let’s denote the events as follows:

• US = the event of getting a coin from the United States

• CA = the event of getting a coin from Canada

• MX = the event of getting a coin from Mexico

• SP = the event of getting a coin from Spain

• FR = the event of getting a coin from France

• IT = the event of getting a coin from Italy

Find the probability for each event.

Solution:

The total number of coins is 150, and we can calculate the number of Italian coins by subtracting the sum of the other coins from the total:

Number of Italian coins = Total number of coins - (US + CA + MX + SP + FR) Number of Italian coins = 150 - (22 + 38 + 20 + 28 + 26) = 16

Now, let’s find the probability for each event:

\[\begin{align*} P(US) &= \dfrac{\text{number of US coins}}{\text{total number of coins}} = \dfrac{22}{150} \\ P(CA) &= \dfrac{\text{number of Canadian coins}}{\text{total number of coins}} = \dfrac{38}{150} \\ P(MX) &= \dfrac{\text{number of Mexican coins}}{\text{total number of coins}} = \dfrac{20}{150} \\ P(SP) &= \dfrac{\text{number of Spanish coins}}{\text{total number of coins}} = \dfrac{28}{150} \\ P(FR) &= \dfrac{\text{number of French coins}}{\text{total number of coins}} = \dfrac{26}{150} \\ P(IT) &= \dfrac{\text{number of Italian coins}}{\text{total number of coins}} = \dfrac{16}{150} \end{align*}\]

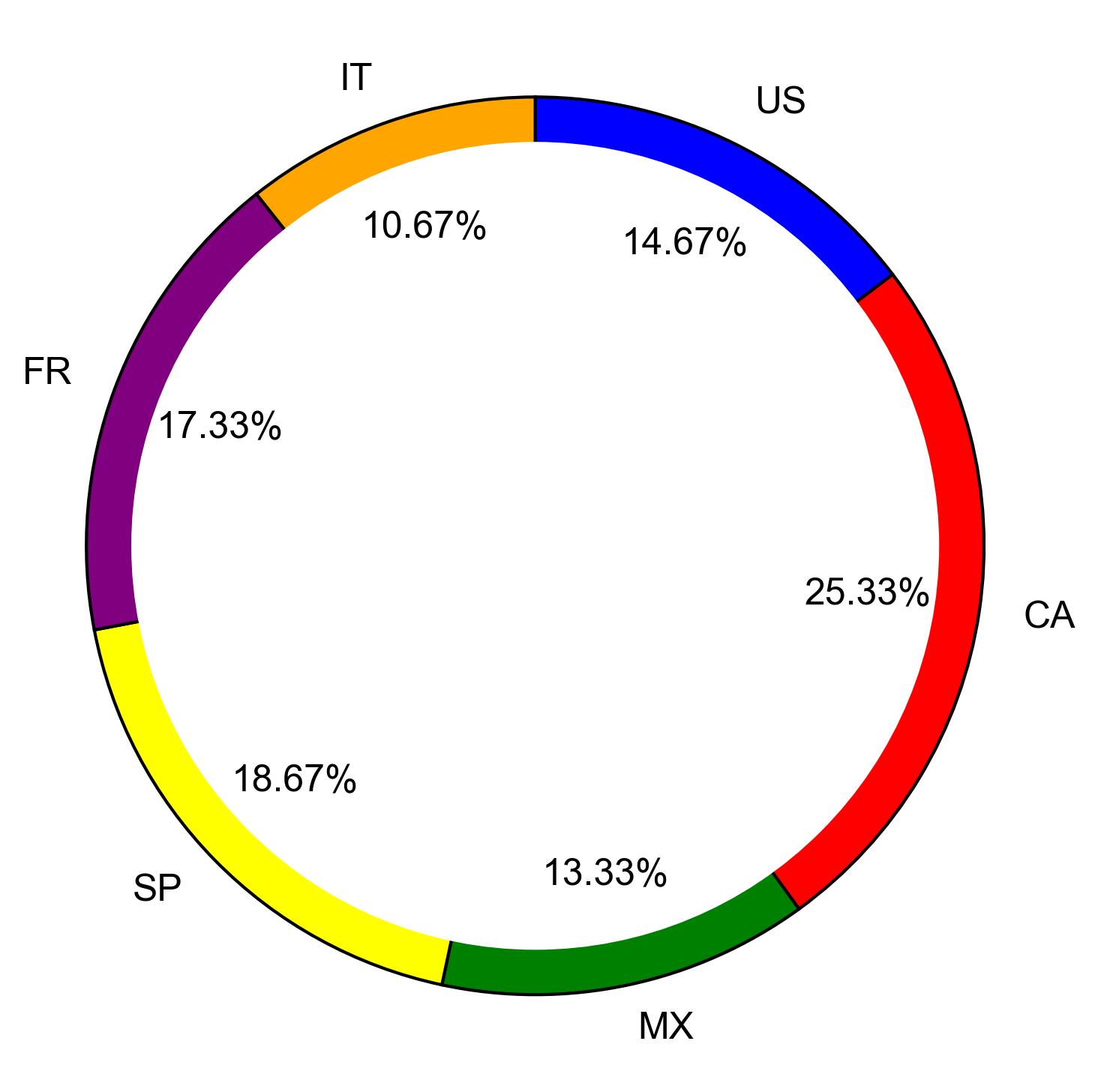
Fig. 3.45 The distribution of 150 vintage coins from various countries. The sections are color-coded and labeled as follows: blue for the United States (US), red for Canada (CA), green for Mexico (MX), yellow for Spain (SP), purple for France (FR), and orange for Italy (IT). Each section’s size represents the proportion of coins from each country, with the percentages annotated inside the plot.

Example 3.22

Imagine a school that has a total of 150 athletes across six different sports teams. The distribution is as follows: 18 in basketball, 40 in soccer, 22 in volleyball, 30 in swimming, 25 in track and field, and the rest are in the tennis team. One athlete is chosen at random to receive a sportsmanship award.

Let’s denote the events as follows:

• B = the event of selecting a basketball player

• S = the event of selecting a soccer player

• V = the event of selecting a volleyball player

• Sw = the event of selecting a swimmer

• T = the event of selecting a track and field athlete

• Te = the event of selecting a tennis player

Find the probability for each event.

Solution:

First, we calculate the number of tennis players by subtracting the sum of the other athletes from the total:

Number of tennis players = Total number of athletes - (B + S + V + Sw + T) Number of tennis players = 150 - (18 + 40 + 22 + 30 + 25) = 15

Now, let’s find the probability for each event:

\[\begin{align*} P(B) &= \dfrac{\text{number of basketball players}}{\text{total number of athletes}} = \dfrac{18}{150} \\ P(S) &= \dfrac{\text{number of soccer players}}{\text{total number of athletes}} = \dfrac{40}{150} \\ P(V) &= \dfrac{\text{number of volleyball players}}{\text{total number of athletes}} = \dfrac{22}{150} \\ P(Sw) &= \dfrac{\text{number of swimmers}}{\text{total number of athletes}} = \dfrac{30}{150} \\ P(T) &= \dfrac{\text{number of track and field athletes}}{\text{total number of athletes}} = \dfrac{25}{150} \\ P(Te) &= \frac{\text{number of tennis players}}{\text{total number of athletes}} = \frac{15}{150} \end{align*}\]

Example 3.23

Imagine a color wheel at the fair with eight sections, each representing a different color:

• B for blue

• R for red

• G for green

• Y for yellow

• O for orange

• P for purple

• W for white

• Bl for black

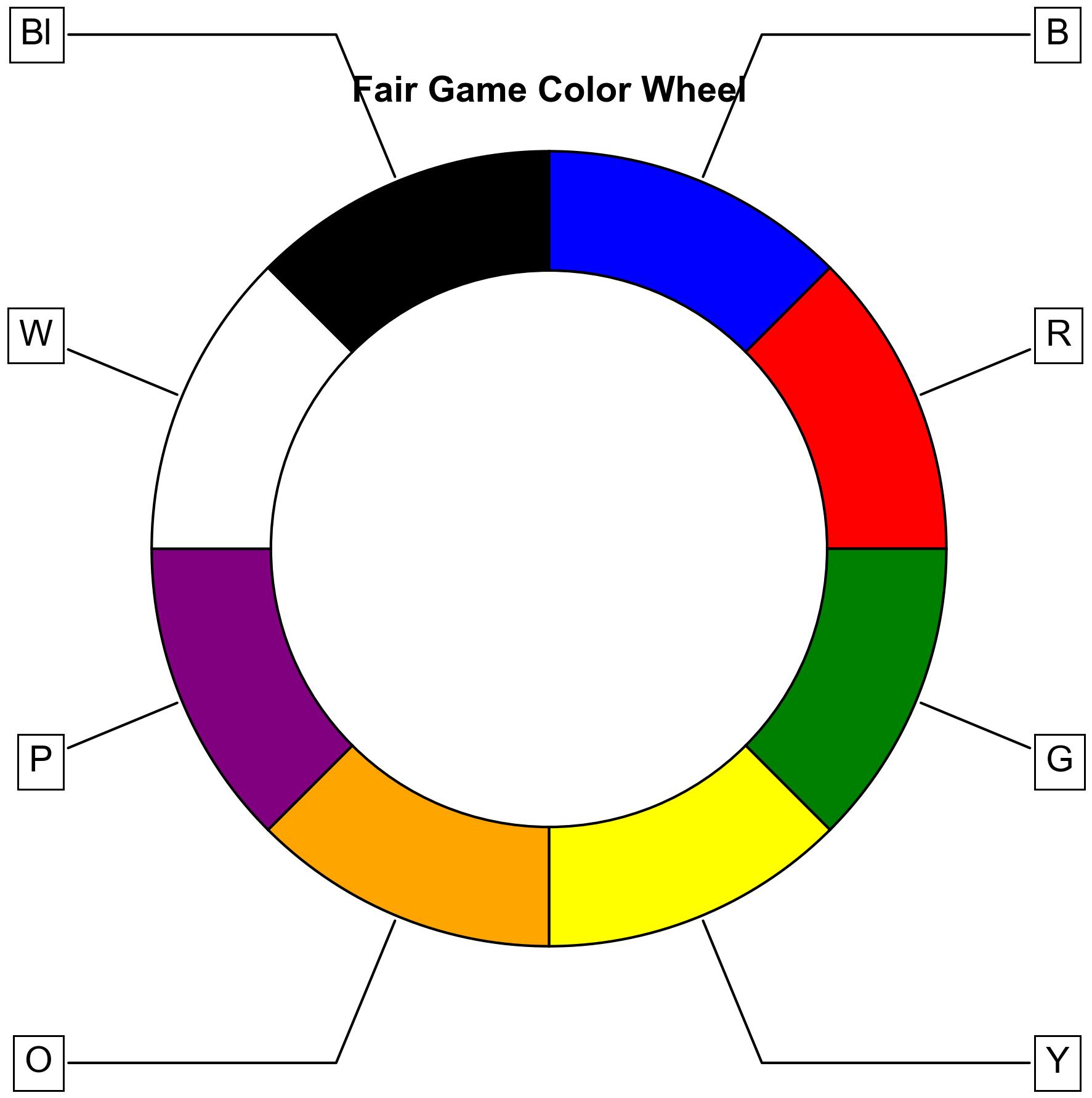
Fig. 3.46 A fair game color wheel, divided into eight equal sections, each labeled with a different color: blue (B), red (R), green (G), yellow (Y), orange (O), purple (P), white (W), and black (Bl). Each section occupies 12.5% of the wheel, indicating an equal probability of landing on any given color.

Special rules:

• Landing on Y (yellow) wins you the grand prize.

• Landing on R (red) means you don’t win anything.

• Landing on O (orange) wins you a small prize.

• Landing on P (purple) allows you to play again.

• Landing on W (white) or Bl (black) doubles the next prize you win.

• Landing on B (blue) or G (green) wins you a medium prize.

Questions:

• a. What is the probability \( P(Y) \) of landing on yellow to win the grand prize?

• b. What is the probability \( P(R) \) of landing on red and winning nothing?

• c. Calculate the probability \( P(O \text{ or } P) \) of landing on either orange or purple to win a small prize or play again.

• d. Find the probability \( P(W \text{ or } Bl) \) of landing on white or black to double your next prize.

Solution:

• a. \( P(Y) = \dfrac{1}{8} \) since there are eight sections.

• b. \( P(R) = \dfrac{1}{8} \) for the same reason.

• c. \( P(O \text{ or } P) = P(O) + P(P) = \dfrac{1}{8} + \dfrac{1}{8} = \dfrac{1}{4} \).

• d. \( P(W \text{ or } Bl) = P(W) + P(Bl) = \dfrac{1}{8} + \dfrac{1}{8} = \dfrac{1}{4} \).