1.1. Definitions of Statistics, Probability, and Key Terms#
1.1.1. Statistics#
Definition - Statistics
Statistics is a branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. It involves the use of mathematical models and statistical methods to draw conclusions about a large set of data (population) based on a smaller set of data (sample) that is observed. The goal of statistics is to provide a systematic approach to understanding and interpreting data, and to make informed decisions based on that data [Vogt, 2005].
Different types of statistics
Biostatistics is the application of statistical methods to the fields of biology and medicine. It involves the use of statistical models and methods to analyze data derived from biological experiments and clinical trials. Biostatistics is used to draw conclusions about the effectiveness of treatments, the safety of drugs, and the causes of diseases [Härdle et al., 2006].
Geostatistics is a branch of statistics that focuses on the analysis of spatial or spatiotemporal datasets related to the study of the solid Earth, its constituent rocks, and the processes that drive their transformations. Geostatistics is used to model and predict the distribution of natural resources, such as oil and gas, and to assess the environmental impact of mining and other activities [Gao, 2021].
Environmental statistics involves the application of statistical techniques to the field of environmental science. It encompasses methodologies for addressing inquiries about both the natural environment in its pristine state and the interaction between humans and the environment. This includes topics such as weather, climate, air, and water quality, as well as studies involving plant and animal populations. Environmental statistics is used to monitor and assess the impact of human activities on the environment, and to develop policies and regulations to protect it [Rong, 2011].
Example 1.1
Weather Forecasting: Probability is used by weather forecasters to assess how likely it is that there will be rain, snow, clouds, etc. on a given day in a certain area.
Sales Tracking: Retail companies often use descriptive statistics like the mean, median, mode, standard deviation, and interquartile range to track the sales behavior of certain products.
Health Insurance: Health insurance companies often use statistics and probability to determine how likely it is that certain individuals will spend a certain amount on healthcare each year.
Traffic: Traffic engineers regularly use statistics to monitor total traffic in different areas of a city, which allows them to decide whether or not they should add or remove roads to optimize traffic flow.
Investing: Investors use statistics and probability to assess how likely it is that a certain investment will pay off.
Medical Studies: Statistics is regularly used in medical studies to understand how different factors are related.
Quality Control: Manufacturers use statistical quality control to ensure that their products meet certain standards of quality.
Sports: Statistics is used extensively in sports to evaluate player performance, predict game outcomes, and analyze team strategies.
Definition - Data
Statistics is a discipline that relies on data as its fundamental building blocks. Data are numerical values or categorical labels that describe the characteristics or outcomes of objects, events, or processes.
Examples of data include:
Numerical data: Heights of students in a classroom, daily temperatures recorded in Calgary, or the number of visitors to a local park.
Categorical data: Types of vehicles registered in Alberta, survey responses about favorite local restaurants, or classifications of different species of plants found in a Calgary botanical garden.
Data can be obtained from various sources, such as:
Routinely kept records: These are data that are systematically collected and stored as part of regular operations or administrative activities. Examples include electronic databases, patient records in healthcare, financial records, and other structured sources of information [Moore, 2009].
Surveys: Surveys are methods of collecting data by directly asking individuals or groups a set of questions. This can be done through interviews, questionnaires, or online forms. Surveys are often used to gather information about opinions, attitudes, behaviors, or characteristics of a specific population [Fowler, 2013].
Experiments: Experiments are techniques of collecting data by conducting controlled procedures to test hypotheses or investigate cause-and-effect relationships. Data obtained from experiments typically involve manipulating variables under controlled conditions and measuring the corresponding outcomes or responses [Montgomery, 2021].
External sources: External sources are data that are available from a wide range of resources beyond the organization or research team. These may include libraries, databases, public records, government reports, academic publications, and other sources of existing data that can be accessed and analyzed for the purpose of a particular study or analysis [Babbie, 2021].
1.1.2. Descriptive statistics#
Definition - Descriptive Statistics
Descriptive statistics is a branch of statistics that deals with the summary and display of data. It uses graphical, numerical, and tabular methods to organize and describe the characteristics or outcomes of a dataset. Descriptive statistics is used to measure the central tendency, variability, and distribution of a dataset, such as the mean, median, mode, range, variance, and standard deviation. It is often used to reduce the complexity of large datasets and to reveal patterns and trends in the data [Moore et al., 2020, Triola, 2007].
Common descriptive statistics methods encompass a variety of analytical approaches, including:
Graphs: These visual representations, including histograms, bar charts, pie charts, and scatter plots, serve to illustrate the distribution, frequency, or relationships within the data.
Numerical measures: Metrics such as the mean, median, mode, standard deviation, and range are employed to convey aspects pertaining to the central tendency, variability, or shape of the dataset.
Tabular methods: Techniques such as frequency tables, cross-tabulations, and contingency tables organize data into categorical frameworks, presenting counts or percentages associated with each category. These methods contribute to a systematic exploration and comprehension of data patterns and relationships.
1.1.3. Inferential statistics#
Definition - Inferential Statistics
Inferential statistics is a branch of statistics that deals with the generalization and inference of data. It uses methods of sampling, estimation, hypothesis testing, and confidence intervals to draw conclusions about a population based on a sample. Inferential statistics is used to test hypotheses and evaluate evidence for decision-making and insights [Agresti et al., 2022, De Veaux, 2022].
A primary application of inferential statistics lies in hypothesis testing—a systematic process employed to assess a proposition concerning a population parameter by leveraging evidence derived from a sample. Beyond hypothesis testing, inferential statistics encompasses the estimation of population parameters, the investigation of relationships between variables, and the generation of predictions grounded in empirical data. This multifaceted approach facilitates a comprehensive understanding of population characteristics and the extrapolation of findings from limited sample observations to broader contexts.
1.1.4. Population and Sample#
Definition - Population and Sample
In statistical analysis, the study of a large group of individuals or objects that share one or more characteristics is a common goal. This group is called the population, and it is the main subject of interest. However, it may not be feasible or practical to collect data from every member of the population. Therefore, a carefully selected, smaller group, called the sample, is used as the basis for empirical data. The choice of the sample is crucial, as it should reflect the diversity and variability of the population. The sampling process allows the researcher to make valid inferences about the population based on the features of the sample [Lohr, 2022].
Fig. 1.1 illustrates the concept of statistical sampling.
Population: The large rectangle on the left represents the entire population, filled with numerous small green circles.
Sample: The smaller rectangle on the right represents a sample, containing only the green circles outlined in black from the population.
Selection: Dotted lines connect each selected circle in the population to its corresponding position in the sample group.
This visual explains how a representative group (sample) is drawn from a larger population for statistical analysis or study purposes. It shows that not all members of a population need to be included in a sample to infer conclusions about the whole population.
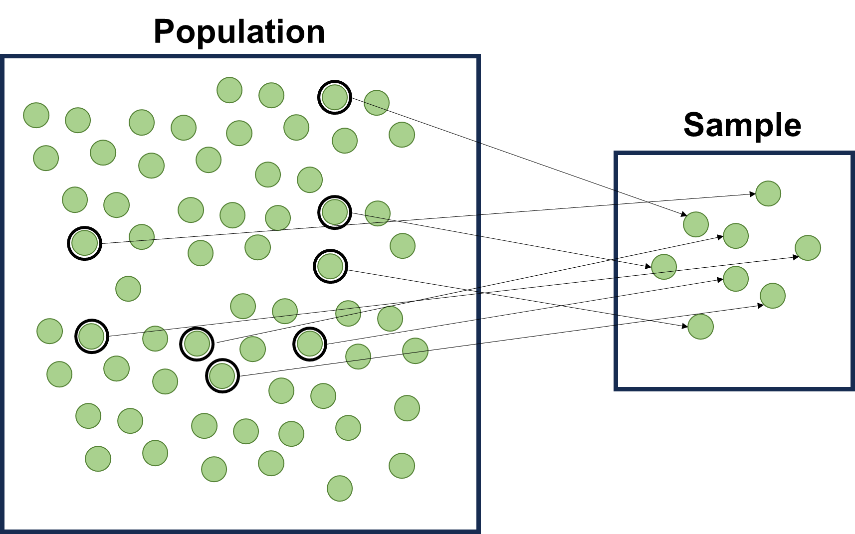
Fig. 1.1 Relationship between population and sample.#
Definition - Proportion for a Sample
In statistical terms, a sample proportion is a ratio of the number of observations in a sample that have a certain attribute to the total number of observations in the sample. It measures the fraction of the sample that belongs to a specific category. Sample proportions are commonly used to estimate population proportions, especially when it is impossible or impractical to collect data from the entire population. This statistical measure allows the researcher to generalize from a sample to a population and to make inferences based on the data [Bluman, 2015, McClave et al., 2022].
Example 1.2
Imagine a survey conducted among 200 students at the University of Calgary to discern their preferred academic subject. If, from the sample of 200, 50 students express a preference for Mathematics, the sample proportion of students favoring Mathematics would be calculated as 50/200 = 0.25 or 25%. This sample proportion serves as an estimate, offering insights into the proportion of students at the University of Calgary who may favor Mathematics, based on the observed preferences within the surveyed sample.
1.1.5. Proportion for a Population#
Definition - Proportion for a Population
In statistical terms, a population proportion is a ratio of the number of elements in a population that have a certain attribute to the total number of elements in the population. It describes the fraction of the population that belongs to a specific category. Population proportions are often unknown and need to be estimated from data collected from a sample [Bluman, 2015, McClave et al., 2022].
Example 1.3
Expanding on Example 1.2, consider a scenario where there are 8,000 students in the entirety of the University of Calgary. If, among this complete student population, 2400 students express a preference for Mathematics, the population proportion of students favoring Mathematics is calculated as 2400/8000 = 0.3 or 30%. This figure serves as a comprehensive measure, representing the proportion of all students at the University of Calgary who prefer Mathematics based on the entire population’s preferences.
Notations for Proportions
In the context of proportions, it is imperative to differentiate between a population proportion (p) and a sample proportion:
x represents the number of successes,
n signifies the sample size,
N denotes the population size,
\(\hat{p} = x/n\) serves as the notation for the sample proportion,
\(p = x/N\) serves as the notation for the population proportion.
Definition - Parameter and Statistic
In the realm of statistics, a parameter is a numerical value or measure that describes a feature of a population. Parameters are often unknown and need to be estimated from data collected from a sample. Parameters include population-level quantities such as means, proportions, or variances.
On the other hand, a statistic is a numerical value or measure that summarizes a feature of a sample. Statistics are used to examine and interpret the data from the sample and to make inferences about the population. Statistics are known values, as they are calculated from the data in the sample [Bluman, 2015, McClave et al., 2022].
Example 1.4
Consider a survey conducted to investigate the preference for two distinct ice cream flavors among a population of children in the city of Calgary.
Parameter - Proportion: In this scenario, the parameter is the proportion of all children in Calgary expressing a preference for a specific ice cream flavor. Assuming our focus is on determining the proportion of children favoring chocolate ice cream:
Suppose Calgary has a total child population of 100,000, and post-survey results reveal that 35,000 children prefer chocolate ice cream. The parameter in question becomes the proportion of children with this preference, calculated as 35,000/100,000 = 0.35 or 35%.
The parameter (proportion) represents the proportion of the entire population of children in the city of Calgary favoring chocolate ice cream, estimated using data from the entire population.
Statistic - Proportion: Conversely, the statistic is the proportion of children participating in the survey who favor chocolate ice cream. If the survey involved 5000 children in Calgary, and 2000 of them expressed a preference for chocolate ice cream, the statistic is the proportion of the sample favoring chocolate ice cream, calculated as 2000/5000 = 0.4 or 40%.
The statistic (proportion) indicates the proportion of the sample of children who participated in the survey and favor chocolate ice cream, calculated based on the data collected from the sample in the city of Calgary.
1.1.6. Representative Statistics#
Definition - Representative Statistics
Representative statistics are those that reflect the features, patterns, or aspects of the whole population from which they are obtained. When statistical values or data samples are representative, they provide a trustworthy and fair description of the population’s features. This ensures that the inferences made from these statistics are valid and reliable for the population, enhancing the quality and credibility of the analytical results [Bluman, 2015, McClave et al., 2022].
Example 1.5
Consider a scenario where a national survey is undertaken in Canada to measure the average income of individuals across the country. In ensuring the representativeness of the sample, a careful selection process encompasses a diverse and random assortment of individuals spanning various regions, age groups, and socioeconomic backgrounds.
For instance, if the calculated average income from this thoughtfully constructed sample closely aligns with the true average income of the entire Canadian population, it signifies the representative nature of the statistical approach. This methodological precision ensures that the insights derived from the sample reliably reflect the broader socioeconomic landscape of Canada, bolstering the accuracy and credibility of the estimated average income.
1.1.7. Non-representative Statistics#
Definition - Non-representative Statistics
Non-representative statistics, also known as biased statistics, are those that do not reflect the features of the whole population. When statistical values or data samples are non-representative, they may have substantial biases that affect the accuracy of the estimates of the population’s features. The non-representativeness reduces the quality and reliability of these statistics, limiting their ability to provide a valid description of the population [Agresti et al., 2022, Bowerman et al., 2018].
Example 1.6
Building upon Example 1.5, if the aforementioned survey exclusively samples individuals from high-income neighborhoods, the derived average income is likely to be higher than the true average income of the entire population. In this scenario, the sample becomes non-representative, and its suitability for generalizing to the entire country’s population is compromised. The inherent bias introduced by disproportionately sampling from high-income areas distorts the accuracy and generalizability of the calculated average income, undermining the survey’s capacity to provide an accurate reflection of the broader socioeconomic landscape of the entire country.
1.1.8. Variable#
Definition - Variable
In statistics, a variable is a feature that can be measured or observed for each individual or object in a population. Variables are denoted by capital letters, such as X and Y, and they represent the characteristics or outcomes of interest. Variables capture the variation or diversity of the data, and they are essential for the analysis and interpretation of the data [Peck et al., 2024, Utts and Heckard, 2022].
Example 1.7
Consider, for instance, X as the height of a person, and Y as the weight of a car.
Variables can broadly be categorized into two fundamental types:
Quantitative variables: These variables involve numerical measurements, such as height or weight, and provide a quantitative basis for analysis.
Qualitative variables: These variables encompass non-numerical attributes, often categorized into distinct groups, providing qualitative insights into characteristics like color or type.
1.1.9. Observational Unit#
Definition - Observational Unit
In statistical terms, an “observational unit” designates the entity or subject upon which observations are conducted or data are collected. It constitutes the individual element or unit of analysis within a dataset. The specific nature of the observational unit is contingent upon the context of the study or research being undertaken [Federer, 1991].
The concept can be clarified through the following examples:
Example - Survey on Car Owners in Calgary:
Observational Unit: Each individual car owner surveyed in the city of Calgary
In this scenario, the observational units are the individual car owners residing in Calgary who participated in the survey. Data may encompass various aspects, such as car make, model, year, mileage, and satisfaction with the vehicle.
Example - Medical Research on Patients in Canada:
Observational Unit: Each patient participating in the study across Canada
In medical research conducted in Canada, the observational units are typically the patients enrolled in the study. Data might include patient characteristics, medical history, treatment regimens, and health outcomes.
Example - Educational Study on Students in Calgary:
Observational Unit: Each student involved in the study in the city of Calgary
In educational research within the city of Calgary, the observational units would be the students who are being studied. Data could include academic performance, attendance, demographic information, and other relevant variables.
Example - Economic Study on Businesses in Canada:
Observational Unit: Each business being analyzed across Canada
In economic research conducted in Canada, the observational units may be individual businesses or companies. Data might cover financial performance, market share, industry type, and other business-related metrics.
