2.3. Measures of Centre of the Data#
2.3.1. Sigma Notation (Summation Notation)#
Consider a sequence of terms:
To sum the first \( n \) terms of this sequence, we use sigma notation, symbolized by the Greek letter \( \Sigma \), which stands for “sum.”
General Form:
The sum of the sequence \( a_1, a_2, a_3, \ldots \) up to the \( n \)th term is written as:
(2.6)#\[\begin{equation} \sum_{i=1}^{n} a_i \end{equation}\]In this expression, \( i \) is the index of summation, starting at 1 and increasing to \( n \).
Examples:
a. Sum of squares of consecutive integers:
\[\begin{equation*} \sum_{k=1}^{m} (k+1)^2 = 2^2 + 3^2 + \ldots + (m+1)^2 \end{equation*}\]b. Sum of a sequence \( f_i \):
\[\begin{equation*} \sum_{i=1}^{m} f_i = f_1 + f_2 + f_3 + \ldots + f_m \end{equation*}\]c. Sum of a sequence divided by \( n \):
\[\begin{equation*} \sum_{i=1}^{m} \dfrac{f_i}{n} = \dfrac{f_1}{n} + \dfrac{f_2}{n} + \dfrac{f_3}{n} + \ldots + \dfrac{f_m}{n} \end{equation*}\]d. Sum of the constant value 2, repeated 6 times:
\[\begin{equation*} \sum_{i=1}^{6} 2 = 2 + 2 + 2 + 2 + 2 + 2 = 12 \end{equation*}\]e. Sum of integers from 5 to 10:
\[\begin{equation*} \sum_{i=5}^{10} i = 5 + 6 + 7 + 8 + 9 + 10 = 45 \end{equation*}\]
Sigma notation streamlines the process of working with sums, especially for large sequences or series, by providing a concise and systematic way to express them. It’s widely used in mathematics to simplify the representation of sums in algebra, calculus, and various other fields of study.
2.3.2. Mean (Average) of a Data Set#
The mean, also known as the average, is a measure of central tendency that provides an estimate of the typical or average value of a data set. It is calculated by summing all the individual observations in the data set and then dividing that sum by the total number of observations.
Calculation and Notation The mean is denoted as:
(2.7)#\[\begin{equation} \text{Mean} = \dfrac{\sum x}{n} = \dfrac{\text{sum of all data values}}{\text{number of data values}} \end{equation}\]Where:
\(x\) represents the individual data values.
\(n\) represents the number of data values in a sample.
Sample Mean: The sample mean, denoted by \(\bar{x}\), is defined as:
(2.8)#\[\begin{equation} \bar{x} = \dfrac{1}{n} \sum_{i=1}^{n} x_i \end{equation}\]Here, \(n\) is the sample size.
Population Mean: The population mean, denoted by \(\mu\), is defined as:
(2.9)#\[\begin{equation} \mu = \dfrac{1}{N} \sum_{i=1}^{N} x_i \end{equation}\]Where:
\(N\) represents the number of data values in the entire population.
Note
Remember:
The symbol \(\Sigma\) denotes the sum of a set of data values.
The variable \(x\) is usually used to represent individual data values.
\(\bar{x}\) (pronounced “x-bar”) represents the mean of a set of sample values.
\(\mu\) (pronounced “mu”) represents the mean of all values in a population.
Remark
Sensitivity to Data Values:
The mean is sensitive to the precise numerical values of all the data points. It takes into account the contribution of each value to the overall average.
Consequently, any changes in the values of the data points directly impact the mean.
Influence of Extreme Values (Outliers):
Extreme values or outliers in the data significantly affect the mean.
Even if these extreme values are not representative of the majority of the data, they can skew the mean towards higher or lower values.
Caution should be exercised when interpreting the mean in the presence of outliers.
Example 2.24
Suppose we have the following data set representing the scores of 10 students in a math quiz:
Calculate the sample mean.
Solution:
To find the sample mean, we’ll follow these steps:
Add up all the individual scores:
\[\begin{equation*} 85 + 92 + 78 + 88 + 95 + 70 + 82 + 91 + 89 + 93 = 863 \end{equation*}\]Divide the sum by the total number of observations (which is 10):
\[\begin{equation*} \bar{x} = \dfrac{863}{10} = 86.3 \end{equation*}\]
The sample mean of the math quiz scores is approximately 86.3.
Example 2.25
You have a data set representing the ages of 10 people. The ages are as follows:
Calculate the sample mean (average) age.
Solution:
Add up all the individual ages:
\[\begin{equation*} 25 + 30 + 22 + 28 + 35 + 40 + 27 + 24 + 29 + 31 = 291 \end{equation*}\]Divide the sum by the total number of observations (which is 10):
\[\begin{equation*} \bar{x} = \dfrac{281}{10} = 29.1 \end{equation*}\]
The sample mean age is approximately 29.1 years.
2.3.3. Calculating the Mean of Grouped Frequency Tables#
Frequency Table:
Start with a frequency table that displays the grouped data intervals (classes) and their corresponding frequencies.
Each interval has a lower boundary and an upper boundary.
Compute Midpoints:
For each interval, calculate the midpoint. The midpoint is the average of the upper and lower bounds of the interval:
(2.10)#\[\begin{equation} \text{Midpoint} = \dfrac{\text{Lower boundary} + \text{Upper boundary}}{2} \end{equation}\]
Multiply Midpoints by Frequencies:
Multiply each midpoint by its corresponding frequency (number of observations in that interval).
Sum up the products:
(2.11)#\[\begin{equation} \sum \left( f\times m\right) \end{equation}\]where:
\(f\) represents the frequency of the interval.
\(m\) represents the midpoint of the interval.
Calculate the Estimated Mean:
Divide the sum of \(f \cdot m\) by the total frequency (sum of all frequencies) to obtain the estimated mean:
(2.12)#\[\begin{equation} \text{Mean of Frequency Table} = \dfrac{\sum \left( f\times m\right)}{\sum f} \end{equation}\]
Example 2.26 (Estimating the Mean from a Grouped Frequency Table)
Consider the following grouped frequency table representing the marks scored in a test by 20 students:
Marks Range |
Frequency |
|---|---|
0-9 |
3 |
10-19 |
5 |
20-29 |
7 |
30-39 |
4 |
40-49 |
1 |
Estimate the mean (average) mark.
Solution:
Find Midpoints:
Calculate the midpoints for each group (class interval). The midpoint is the average of the upper and lower bounds of each interval.
Midpoint of 0-9: \(\dfrac{0 + 9}{2} = 4.5\)
Midpoint of 10-19: \(\dfrac{10 + 19}{2} = 14.5\)
Midpoint of 20-29: \(\dfrac{20 + 29}{2} = 24.5\)
Midpoint of 30-39: \(\dfrac{30 + 39}{2} = 34.5\)
Midpoint of 40-49: \(\dfrac{40 + 49}{2} = 44.5\)
Multiply Midpoints by Frequencies:
Multiply each midpoint by its corresponding frequency:
\(4.5 \times 3 = 13.5\)
\(14.5 \times 5 = 72.5\)
\(24.5 \times 7 = 171.5\)
\(34.5 \times 4 = 138\)
\(44.5 \times 1 = 44.5\)
Find the Total:
Add up the products:
\[\begin{equation*} \text{Total} = 13.5 + 72.5 + 171.5 + 138 + 44.5 = 440\end{equation*}\]
Estimate the Mean:
Divide the total by the sum of frequencies (which is 20 in this case):
\[\begin{equation*} \text{Estimated Mean} = \dfrac{\text{Total}}{20} = \dfrac{440}{20} = 22\end{equation*}\]
The estimated mean mark is approximately 22.
Example 2.27 (Estimating the Mean from a Grouped Frequency Table)
Consider the following grouped frequency table representing the heights (in centimeters) of 30 students:
Height Range |
Frequency |
|---|---|
150-159 |
5 |
160-169 |
12 |
170-179 |
8 |
180-189 |
4 |
190-199 |
1 |
Estimate the mean (average) height.
Solution:
Find Midpoints:
Calculate the midpoints for each group (class interval). The midpoint is the average of the upper and lower bounds of each interval.
Midpoint of 150-159: \(\dfrac{150 + 159}{2} = 154.5\)
Midpoint of 160-169: \(\dfrac{160 + 169}{2} = 164.5\)
Midpoint of 170-179: \(\dfrac{170 + 179}{2} = 174.5\)
Midpoint of 180-189: \(\dfrac{180 + 189}{2} = 184.5\)
Midpoint of 190-199: \(\dfrac{190 + 199}{2} = 194.5\)
Multiply Midpoints by Frequencies:
Multiply each midpoint by its corresponding frequency:
\(154.5 \times 5 = 772.5\)
\(164.5 \times 12 = 1974\)
\(174.5 \times 8 = 1396\)
\(184.5 \times 4 = 738\)
\(194.5 \times 1 = 194.5\)
Find the Total:
Add up the products:
\[\begin{equation*} \text{Total} = 772.5 + 1974 + 1396 + 738 + 194.5 = 5075 \end{equation*}\]
Estimate the Mean:
Divide the total by the sum of frequencies (which is 30 in this case):
\[\begin{equation*} \text{Estimated Mean} = \dfrac{\text{Total}}{30} = \dfrac{5075}{30} = 169.17 \end{equation*}\]
The estimated mean height is approximately 169.17 centimeters.
2.3.4. Median of a Data Set#
The median is a measure of central tendency that identifies the middle position within a dataset. When the observations are sorted in ascending order, the median represents the point at which half of the data lies above and half below. It is also referred to as the 50th percentile or the second quartile (\(Q_2\)) in the distribution of data (we will dicuss percentiles and quartiles later on).
Comparing Sample and Population Medians:
The sample median is a statistic that estimates the population median when the full population data is not available.
The population median is a parameter that divides the entire population into two halves, with one half having values below the median and the other half above it.
The sample median is a reliable estimator of the population median, particularly when the sample is representative of the population and is large enough. It is robust against outliers and skewed data, making it a preferred measure over the mean in such cases.
Note
In statistics, the symbol for the population median is not universally standardized. However, it is common to use Greek letters for population parameters. While there is no widely accepted symbol for the population median, some sources suggest using the Greek letter eta (\(\eta\)). Another suggestion is to use theta (\(\theta\)), as indicated in some textbooks.
Example 2.28
Suppose we have a sample of data points:
a. Calculate the median of this sample.
b. Explain how you arrived at your answer.
Solution:
a. To find the median, we first arrange the data points in ascending order:
Since there are 5 data points, the median will be the middle value. In this case, the middle value is the third data point, which is 20.
Therefore, the median of the sample is 20.

Fig. 2.15 Visualization of median for Example 2.28.#
b. Explanation:
The median is the value that separates the lower half of the data from the upper half.
Since we have an odd number of data points, the median is the middle value.
In this sample, the middle value is 20.
Example 2.29
Suppose we have another sample of data points:
Solution:
Arrange the data points in ascending order:
Since there are 4 data points, the median will be the average of the two middle values. In this case, the middle values are 18 and 22.
Therefore, the median of the sample is 20.

Fig. 2.16 Visualization of median for Example 2.29.#
Explanation:
The median is the value that separates the lower half of the data from the upper half.
Since we have an even number of data points, we take the average of the two middle values.
In this sample, the middle values are 18 and 22, so the median is 20.
Example 2.30
In a quality control process at an engineering manufacturing facility, a sample of 10 steel rods was selected to measure their tensile strength in megapascals (MPa). The tensile strength is a critical parameter that determines the rod’s ability to withstand tension without failure. The following data points represent the tensile strength measurements of the sampled steel rods:
Calculate the median tensile strength of the sample and explain the process used to arrive at the answer.
Solution: To find the median of the given sample, we follow these steps:
Arrange the Data in Ascending Order: The data is already arranged in ascending order, which is necessary for finding the median.
Determine the Median Position: Since there are 10 data points, which is an even number, the median will be the average of the 5th and 6th values.
Calculate the Median: The 5th value is 620 MPa, and the 6th value is 640 MPa. The median (M) is the average of these two values:

Fig. 2.17 Visualization of median for Example 2.30.#
Therefore, the median tensile strength of the sample is 630 MPa. This value represents the middle tensile strength in the dataset, meaning that half of the steel rods have a tensile strength below 630 MPa, and the other half have a tensile strength above 630 MPa. This measure is particularly useful in quality control to understand the central tendency of the tensile strength among the sampled rods.
Example 2.31
In a civil engineering study, the stability of a newly designed bridge is being tested under various load conditions. Engineers have measured the maximum load capacity (in tons) that the bridge can withstand without structural failure during 10 different test scenarios. The following data points represent the maximum load capacity recorded for each test:
Calculate the median maximum load capacity of the bridge from the sample data and provide a detailed explanation of your calculation process.
Solution: To calculate the median from the given dataset, we follow these steps:
Arrange the Data in Ascending Order: The data is already listed in ascending order, which is the first step in finding the median.
Determine the Median Position: Since the number of data points is 10, an even number, the median will be the average of the 5th and 6th data points.
Calculate the Median: The 5th data point is 65 tons, and the 6th data point is 70 tons. The median (M) is calculated as the average of these two values:

Fig. 2.18 Visualization of median for Example 2.31.#
Therefore, the median maximum load capacity of the bridge is 67.5 tons. This value indicates that half of the test scenarios resulted in a maximum load capacity below 67.5 tons, and the other half resulted in a capacity above 67.5 tons. This median value is crucial for engineers to understand the bridge’s performance under varying load conditions and to ensure its safety and reliability.
Remark
Mean:
The mean is calculated by adding up all the values in a dataset and then dividing by the total number of values.
It is influenced by the precise numerical values of all data points, including outliers or extreme values.
The mean can be sensitive to extreme values, pulling it toward those outliers.
Median:
The median is the middle value when the data points are arranged in ascending or descending order.
Unlike the mean, the median is not affected by the precise numerical values of outliers or extreme values.
It only considers the relative position of the data points.
The median is generally a better measure of center when dealing with data that contains extreme values or outliers because it provides a more robust representation of the central tendency.
2.3.5. Mode of a Data Set#
Mode:
The mode of a dataset is the value (or values) that appear with the highest frequency.
In other words, it is the value that occurs most frequently compared to other values in the dataset.
Example 2.32 (Multimodal Dataset)
Consider the following dataset representing the number of hours students spend studying for an exam:
Calculate the mode(s) for this dataset. Is it bimodal?
Solution:
Value 2 appears 3 times.
Value 3 appears 3 times.
Value 4 appears 3 times.
Value 5 appears 2 times.
Since both 2, 3, and 4 occur with the highest frequency (3 times each), this dataset is bimodal.
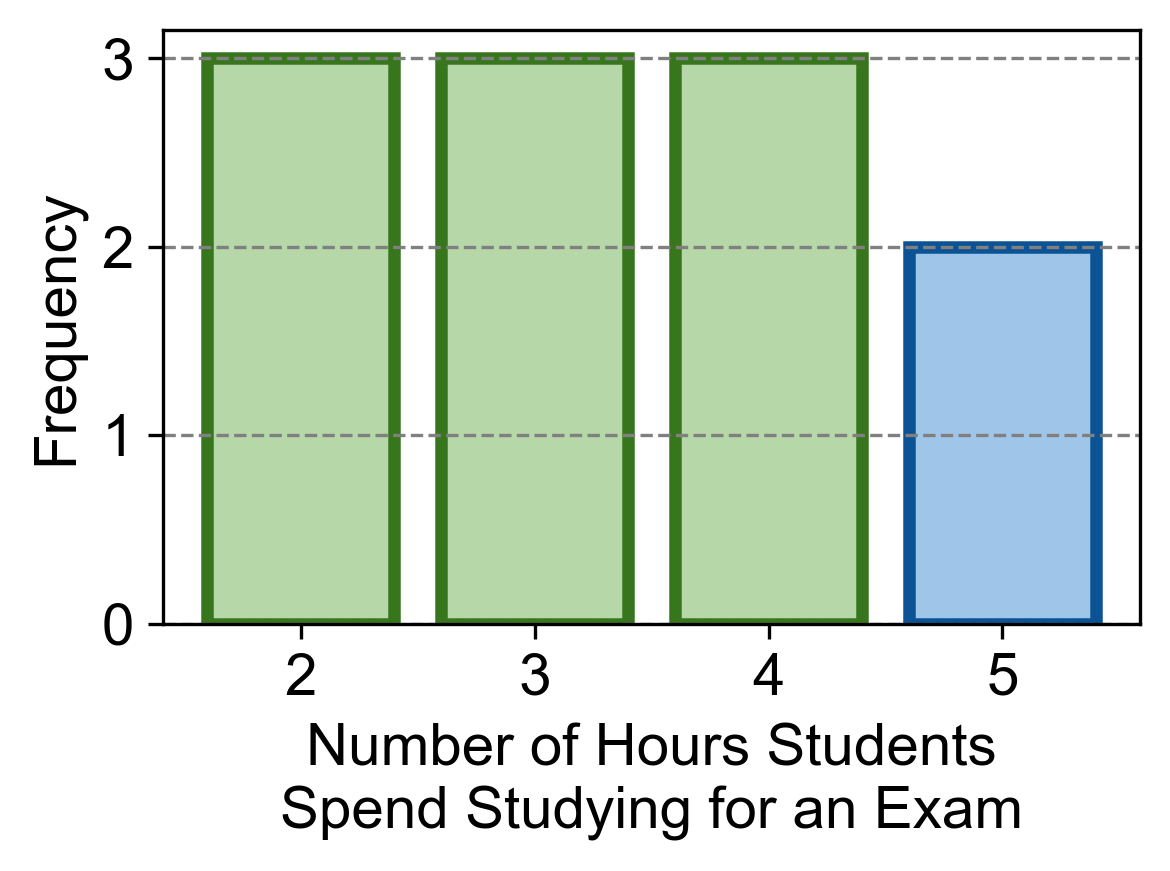
Fig. 2.19 Visualization of median for Example 2.32.#
Example 2.33 (Multimodal Dataset)
Consider the following dataset representing the number of pets owned by households in a neighborhood:
Calculate the mode(s) for this dataset. Is it multimodal?
Solution:
Value 2 appears 4 times.
Value 3 appears 4 times.
Value 4 appears 4 times.
Since three different values (2, 3, and 4) occur with the highest frequency (4 times each), this dataset is multimodal.
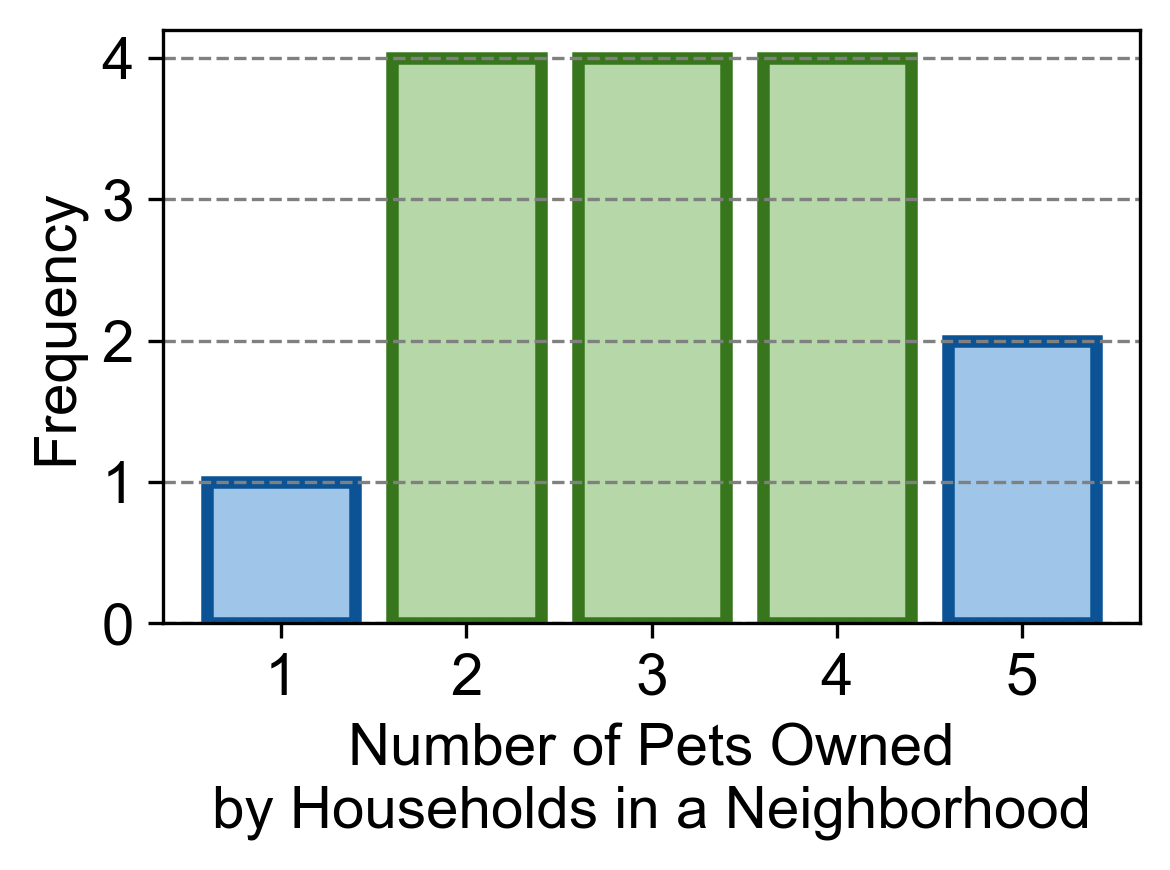
Fig. 2.20 Visualization of the mode for Example 2.33.#
2.3.6. Midrange of a Data Set#
The midrange of a dataset is a central measure that represents the value situated exactly midway between the maximum and minimum values present in the original data set.
To compute the midrange, follow these steps:
Add the maximum data value to the minimum data value.
Divide the resulting sum by 2 using the following formula:
(2.13)#\[\begin{equation} \text{Midrange} = \dfrac{\text{maximum data value} + \text{minimum data value}}{2} \end{equation}\]
Example 2.34
Consider the following dataset representing the ages of a group of people (in years):
Find the (a) mean, (b) median, (c) mode, and (d) midrange.
Solution:
a. Mean:
Sum of all ages: \(25 + 30 + 22 + 28 + 35 + 30 + 22 + 40 + 28 + 25 = 285\)
Total number of people: \(10\)
Mean: \(\dfrac{285}{10} = 28.5\)
b. Median:
Arrange the ages in ascending order: \(22, 22, 25, 25, 28, 28, 30, 30, 35, 40\)
Since there are \(10\) values, the median is the average of the \(5\)th and \(6\)th values: \(\dfrac{28 + 28}{2} = 28\)
c. Mode:
Value \(22\) appears \(2\) times.
Value \(25\) appears \(2\) times.
Value \(28\) appears \(2\) times.
Value \(30\) appears \(2\) times.
Therefore, this dataset is multimodal with modes \(22\), \(25\), \(28\), and \(30\).
d. Midrange:
Maximum age: \(40\)
Minimum age: \(22\)
Midrange: \(\dfrac{40 + 22}{2} = 31\)

Fig. 2.21 Visualization of the midrange for Example 2.34.#
Example 2.35
Suppose we have the following dataset representing the test scores (out of 100) of a group of students:
Calculate the following measures:
a. Mean
b. Median
c. Mode
d. Midrange
Solution:
a. Mean:
Sum of all test scores: \(78 + 85 + 92 + 70 + 88 + 78 + 95 + 82 + 88 + 90 = 846\)
Total number of students: \(10\)
Mean: \(\dfrac{846}{10} = 84.6\)
b. Median:
Arrange the test scores in ascending order: \(70, 78, 78, 82, 85, 88, 88, 90, 92, 95\)
Since there are \(10\) values, the median is the average of the \(5\)th and \(6\)th values: \(\dfrac{85 + 88}{2} = 86.5\)

Fig. 2.22 Visualization of median for Example 2.35.#
c. Mode:
Value \(78\) appears \(2\) times.
Value \(88\) appears \(2\) times.
Therefore, this dataset is bimodal with modes \(78\) and \(88\).
d. Midrange:
Maximum test score: \(95\)
Minimum test score: \(70\)
Midrange: \(\dfrac{95 + 70}{2} = 82.5\)

Fig. 2.23 Visualization of midrange for Example 2.35.#
Summary
Mean (Average):
The mean, denoted as \(\bar{x}\), is calculated as the sum of all data values divided by the total number of data points.
It represents the central tendency of the data.
Formula: \(\bar{x} = \dfrac{1}{n}\sum_{i=1}^{n} x_i\)
The mean is unique for a given sample data.
Median:
The sample median, denoted by \(\widetilde{x}\), is determined as follows:
Arrange the \(n\) data values in increasing order.
If the sample size \(n\) is odd, the median is the value in the middle position.
If the sample size \(n\) is even, it is the average of the values in the two middle positions.
The median represents the middlemost sample observation in sorted data.
Mode:
The mode is the most frequently occurring sample observation.
A dataset can have no mode, be unimodal (one mode), bimodal (two modes), or multimodal (more than two modes).
