2.7. Box Plots

2.7.1. Quartiles

Quartiles are statistical measures that divide a dataset into four equal parts. They help us understand the distribution of data by identifying key points within it.

1. \(Q_1\) (First Quartile):

   • Also known as the 25th percentile \(P_{25}\).

   • Separates the bottom 25% of the sorted values from the top 75%.

   • At least 25% of the sorted values are less than or equal to \(Q_1\), and at least 75% are greater than or equal to \(Q_1\).

   • Mathematically: \(Q_1 = P_{25}\).

2. \(Q_2\) (Second Quartile):

   • Same as the median \(P_{50}\).

   • Separates the bottom 50% of the sorted values from the top 50%.

   • Mathematically: \(Q_2 = P_{50}\).

3. \(Q_3\) (Third Quartile):

   • Also known as the 75th percentile \(P_{75}\).

   • Separates the bottom 75% of the sorted values from the top 25%.

   • At least 75% of the sorted values are less than or equal to \(Q_3\), and at least 25% are greater than or equal to \(Q_3\).

   • Mathematically: \(Q_3 = P_{75}\).

Example 2.42

Suppose we have the following data set representing the ages of a group of people (in years):

18, 22, 25, 30, 35, 40, 42, 48, 50, 55

Find the quartiles (\(Q_1\), \(Q_2\), and \(Q_3\)) for this data set.

Solution: To find the quartiles of a dataset, we first need to organize the data in ascending order. Then, we can determine the values that divide the data into four equal parts.

1. Organize the Data:

   • The ages of the group of people are:

Index	1	2	3	4	5	6	7	8	9	10
Number	18	22	25	30	35	40	42	48	50	55

2. Find the Index:

   • For \(Q_1\) (25th percentile), \(Q_2\) (50th percentile, median), and \(Q_3\) (75th percentile), we need to find the indices corresponding to these percentiles.

3. Identify the Quartile Values:

   • For \(Q_1\) (25th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(10 - 1) \times 25}{100} + 1 = 3.25\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_1 = P_{25} = 25 + 0.25 \times (30 - 25) = 25 + 0.25 \times 5 = 26.25\end{equation*}\]

   • For \(Q_2\) (50th percentile, Median):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(10 - 1) \times 50}{100} + 1 = 5.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_2 = P_{50} = 35 + 0.5 \times (40 - 35) = 35 + 0.5 \times 5 = 37.5\end{equation*}\]

   • For \(Q_3\) (75th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(10 - 1) \times 75}{100} + 1 = 7.75\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_3 = P_{75} = 42 + 0.75 \times (48 - 42) = 42 + 0.75 \times 6 = 46.5\end{equation*}\]

   Therefore, the quartiles for this dataset are:

   \[\begin{equation*}Q_1 = 26.25, \, Q_2 = 37.5, \, \text{and} \, Q_3 = 46.5\end{equation*}\]

Fig. 2.45 Visualizing Percentiles for Example 2.42.

Example 2.43

Suppose we have the following data set representing the test scores (out of 100) of a group of students:

65, 72, 78, 82, 88, 92, 95, 98

Find the quartiles (\(Q_1\), \(Q_2\), and \(Q_3\)) for this data set.

Solution: To find the quartiles of a dataset, we first need to organize the data in ascending order. Then, we can determine the values that divide the data into four equal parts.

1. Organize the Data:

   • The test scores of the group of students are:

Index	1	2	3	4	5	6	7	8
Number	65	72	78	82	88	92	95	98

2. Find the Index:

   • For \(Q_1\) (25th percentile), \(Q_2\) (50th percentile, median), and \(Q_3\) (75th percentile), we need to find the indices corresponding to these percentiles.

3. Identify the Quartile Values:

   • For \(Q_1\) (25th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(8 - 1) \times 25}{100} + 1 = 2.75\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_1 = P_{25} = 72 + 0.75 \times (78 - 72) = 72 + 0.75 \times 6 = 76.5\end{equation*}\]

   • For \(Q_2\) (50th percentile, Median):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(8 - 1) \times 50}{100} + 1 = 4.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_2 = P_{50} = 82 + 0.5 \times (88 - 82) = 82 + 0.5 \times 6 = 85.0\end{equation*}\]

   • For \(Q_3\) (75th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(8 - 1) \times 75}{100} + 1 = 6.25\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_3 = P_{75} = 92 + 0.25 \times (95 - 92) = 92 + 0.25 \times 3 = 92.75\end{equation*}\]

   Therefore, the quartiles for this dataset are:

   \[\begin{equation*}Q_1 = 76.5, \, Q_2 = 85.0, \, \text{and} \, Q_3 = 92.75\end{equation*}\]

Fig. 2.46 Visualizing Percentiles for Example 2.43.

Example 2.44

Suppose we have the following data set representing the heights (in centimeters) of a group of individuals:

160, 165, 170, 175, 180, 185, 190, 195

Solution: To find the quartiles of a dataset, we first need to organize the data in ascending order. Then, we can determine the values that divide the data into four equal parts.

1. Organize the Data:

   • The heights (in centimeters) of the group of individuals are:

Index	1	2	3	4	5	6	7	8
Number	160	165	170	175	180	185	190	195

2. Find the Index:

   • For \(Q_1\) (25th percentile), \(Q_2\) (50th percentile, median), and \(Q_3\) (75th percentile), we need to find the indices corresponding to these percentiles.

3. Identify the Quartile Values:

   • For \(Q_1\) (25th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(8 - 1) \times 25}{100} + 1 = 2.75\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_1 = P_{25} = 165 + 0.75 \times (170 - 165) = 165 + 0.75 \times 5 = 168.75\end{equation*}\]

   • For \(Q_2\) (50th percentile, Median):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(8 - 1) \times 50}{100} + 1 = 4.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_2 = P_{50} = 175 + 0.5 \times (180 - 175) = 175 + 0.5 \times 5 = 177.5\end{equation*}\]

   • For \(Q_3\) (75th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(8 - 1) \times 75}{100} + 1 = 6.25\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_3 = P_{75} = 185 + 0.25 \times (190 - 185) = 185 + 0.25 \times 5 = 186.25\end{equation*}\]

   Therefore, the quartiles for this dataset are:

   \[\begin{equation*}Q_1 = 168.75, \, Q_2 = 177.5, \, \text{and} \, Q_3 = 186.25\end{equation*}\]

Fig. 2.47 Visualizing Percentiles for Example 2.44.

2.7.2. Box plots

Definition - Box plots

A box plot, also known as a box-and-whisker plot, is a powerful graphical tool for summarizing and visualizing the distribution of a dataset. It provides a concise representation of key statistical measures and highlights the spread of data points.

A break down the essential components of box plots:

1. Box:

   • The central box represents the interquartile range (IQR), which contains the middle 50% of the data.

   • The box spans from the first quartile (\(Q_1\)) to the third quartile (\(Q_3\)).

   • The length of the box indicates the variability within this middle range.

2. Whiskers:

   • The whiskers extend from the box to the minimum and maximum values within a certain range.

   • The lower whisker reaches the minimum value, and the upper whisker reaches the maximum value.

   • Whiskers provide insights into the data’s spread beyond the IQR.

3. Median (\(Q_2\)):

   • Inside the box, a horizontal line represents the median (\(Q_2\)).

   • The median divides the data into two equal halves: 50% above and 50% below.

4. Outliers (will discuss in Section 2.7.4):

   • Data points lying outside the whiskers are considered outliers.

   • Outliers may indicate extreme values or anomalies in the dataset.

Fig. 2.48 Components of a boxplot.

Why Use Box Plots?

• Visual Comparison: Box plots allow us to compare distributions across different groups or categories.

• Identifying Skewness: Skewed data can be detected by observing the box’s asymmetry.

• Spotting Outliers: Outliers are easily identifiable beyond the whiskers.

• Data Concentration: The box highlights where most data points lie.

2.7.3. 5-Number Summary and Box Plots

• 1. 5-Number Summary: The 5-number summary provides a concise overview of a dataset’s distribution. It consists of the following five values:

  1. Minimum: The smallest value in the dataset.

  2. First Quartile (\(Q_1\)): The median of the lower half of the data. It represents the 25th percentile.

  3. Second Quartile (\(Q_2\)): The same as the median. It divides the data into two equal halves (50th percentile).

  4. Third Quartile (\(Q_3\)): The median of the upper half of the data. It represents the 75th percentile.

  5. Maximum: The largest value in the dataset.

Fig. 2.49 Minimum value, \(Q_1\), \(Q_2\), \(Q_3\), Maximum value

• 2. Procedure for Constructing a Box Plot: A box plot visually represents the 5-number summary. Follow these steps to create a box plot:

  1. Find the 5-Number Summary:

     • Calculate the minimum, \(Q_1\), \(Q_2\) (median), \(Q_3\), and maximum values from your dataset.

     • These values provide essential insights into the spread and central tendency of the data.

  2. Construct the Box Plot:

     • Start by drawing a line segment extending from the minimum data value to the maximum data value. This line represents the entire data range.

     • Next, create a box (rectangle):

       • The left edge of the box corresponds to \(Q_1\).

       • The right edge of the box corresponds to \(Q_3\).

       • The width of the box represents the interquartile range (IQR), which contains the middle 50% of the data.

     • Inside the box, draw a vertical line at the value of \(Q_2\) (the median).

     • The whiskers (lines extending from the box) connect to the minimum and maximum values within a certain range.

     • Any data points beyond the whiskers are considered outliers.

  Box plots allow us to quickly assess data concentration, identify skewness, and spot extreme values. They are valuable tools for exploratory data analysis and comparisons across different groups or categories.

Example 2.45

Suppose we have the following dataset representing the ages of 10 individuals (in years):

25, 28, 30, 32, 35, 38, 40, 42, 45, 50

Find the 5-number summary and then generate a boxplot for the provided data.

Solution: To find the 5-number summary for the given dataset representing the ages of 10 individuals, we need to find the minimum, first quartile (\(Q_1\)), median (\(Q_2\)), third quartile (\(Q_3\)), and maximum values.

1. Organize the Data:

   • The ages of the 10 individuals are:

Index	1	2	3	4	5	6	7	8	9	10
Number	25	28	30	32	35	38	40	42	45	50

2. Calculate the Quartiles:

   • Using the formula:

     \[\begin{equation*}I = \dfrac{(10 - 1) \times q}{100} + 1\end{equation*}\]

   • For \(Q_1\) (25th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(10 - 1) \times 25}{100} + 1 = 3.25\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_1 = P_{25} = 30 + 0.25 \times (32 - 30) = 30 + 0.25 \times 2 = 30.5\end{equation*}\]

   • For \(Q_2\) (50th percentile, Median):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(10 - 1) \times 50}{100} + 1 = 5.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_2 = P_{50} = 35 + 0.5 \times (38 - 35) = 35 + 0.5 \times 3 = 36.5\end{equation*}\]

   • For \(Q_3\) (75th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(10 - 1) \times 75}{100} + 1 = 7.75\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_3 = P_{75} = 40 + 0.75 \times (42 - 40) = 40 + 0.75 \times 2 = 41.5\end{equation*}\]

3. Calculate the Minimum and Maximum:

   • Minimum: 25

   • Maximum: 50

The 5-number summary for the given dataset is: [25, 30.5, 36.5, 41.5, 50].

Fig. 2.50 Visualizing Percentiles for Example 2.45.

Now, let’s generate a boxplot for the provided data.

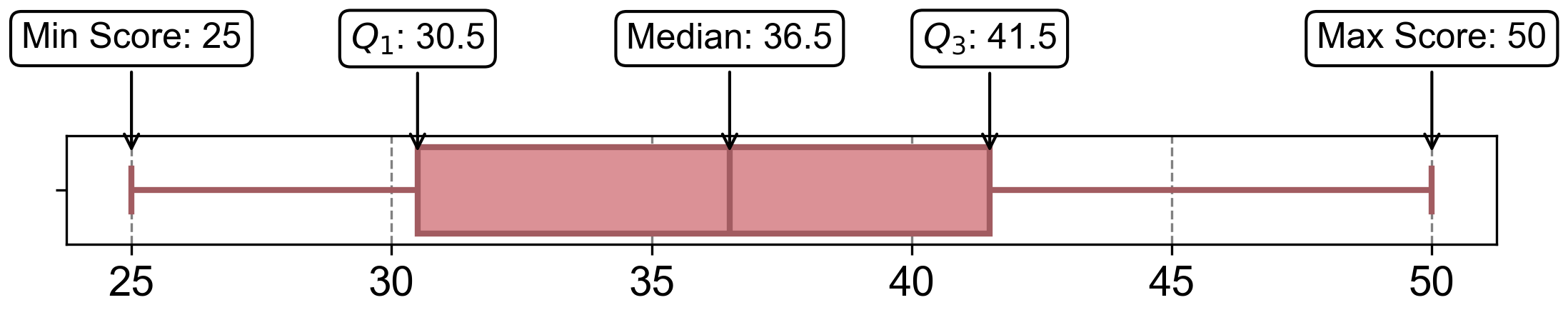
Fig. 2.51 Visualizing boxplot for Example 2.45.

Example 2.46

Suppose we have the following dataset representing the ages of 10 individuals (in years):

25, 28, 30, 32, 35, 38, 40, 42, 45, 50, 55

Find the 5-number summary and then generate a boxplot for the provided data.

Solution: To find the 5-number summary for the given dataset representing the ages of 10 individuals, we need to find the minimum, first quartile (\(Q_1\)), median (\(Q_2\)), third quartile (\(Q_3\)), and maximum values.

1. Organize the Data:

   • The ages of the 10 individuals are:

Index	1	2	3	4	5	6	7	8	9	10	11
Number	25	28	30	32	35	38	40	42	45	50	55

2. Calculate the Quartiles:

   • Using the formula:

     \[\begin{equation*}I = \dfrac{(11 - 1) \times q}{100} + 1\end{equation*}\]

   • For \(Q_1\) (25th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(11 - 1) \times 25}{100} + 1 = 3.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_1 = P_{25} = 30 + 0.5 \times (32 - 30) = 30 + 0.5 \times 2 = 31.0\end{equation*}\]

   • For \(Q_2\) (50th percentile, Median):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(11 - 1) \times 50}{100} + 1 = 6.0\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_2 = P_{50} = 38 + 0.0 \times (38 - 38) = 38 + 0.0 \times 0 = 38.0\end{equation*}\]

   • For \(Q_3\) (75th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(11 - 1) \times 75}{100} + 1 = 8.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_3 = P_{75} = 42 + 0.5 \times (45 - 42) = 42 + 0.5 \times 3 = 43.5\end{equation*}\]

3. Calculate the Minimum and Maximum:

   • Minimum: 25

   • Maximum: 55

The 5-number summary for the given dataset is: [25, 31.0, 38.0, 43.5, 55].

Fig. 2.52 Visualizing Percentiles for Example 2.46.

Now, let’s generate a boxplot for the provided data.

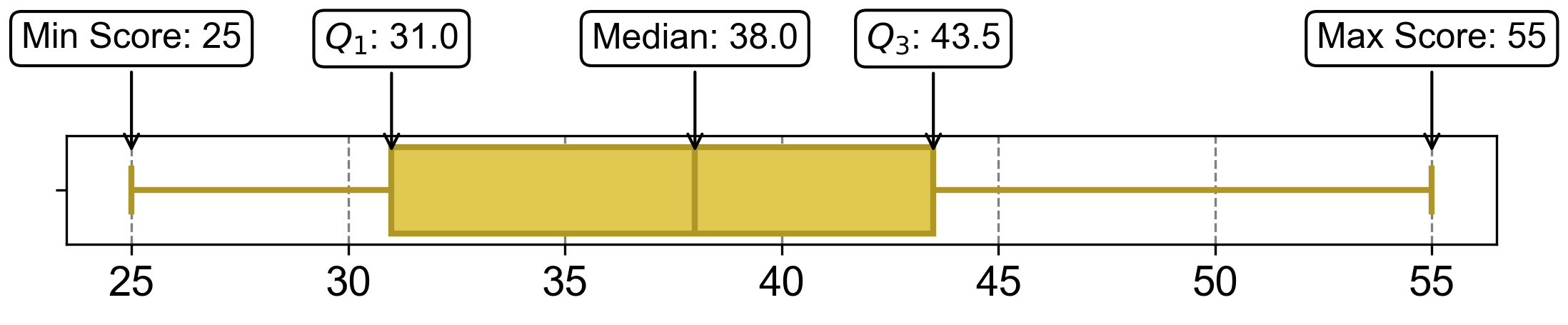
Fig. 2.53 Visualizing boxplot for Example 2.46.

Example 2.47

Suppose we have the following dataset representing the annual rainfall (in millimeters) recorded in a particular region over the last 10 years:

1080, 950, 1230, 1100, 1150, 980, 1020, 1175, 1210, 1160

Your task is to find the 5-number summary of this dataset and then generate a boxplot to visually represent the distribution of the annual rainfall.

Solution: To find the 5-number summary for the given dataset representing the annual rainfall recorded in a particular region over the last 10 years, we need to find the minimum, first quartile (\(Q_1\)), median (\(Q_2\)), third quartile (\(Q_3\)), and maximum values.

1. Organize the Data:

   • The annual rainfall (in millimeters) recorded over the last 10 years are:

Index	1	2	3	4	5	6	7	8	9	10
Number	1080	950	1230	1100	1150	980	1020	1175	1210	1160

2. Calculate the Quartiles:

   • Using the formula:

     \[\begin{equation*}I = \dfrac{(10 - 1) \times q}{100} + 1\end{equation*}\]

   • For \(Q_1\) (25th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(10 - 1) \times 25}{100} + 1 = 3.25\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_1 = P_{25} = 1020 + 0.25 \times (1080 - 1020) = 1020 + 0.25 \times 60 = 1035.0\end{equation*}\]

   • For \(Q_2\) (50th percentile, Median):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(10 - 1) \times 50}{100} + 1 = 5.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_2 = P_{50} = 1100 + 0.5 \times (1150 - 1100) = 1100 + 0.5 \times 50 = 1125.0\end{equation*}\]

   • For \(Q_3\) (75th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(10 - 1) \times 75}{100} + 1 = 7.75\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_3 = P_{75} = 1160 + 0.75 \times (1175 - 1160) = 1160 + 0.75 \times 15 = 1171.25\end{equation*}\]

3. Calculate the Minimum and Maximum:

   • Minimum: 950

   • Maximum: 1230

The 5-number summary for the given dataset is: [950, 1035.0, 1125.0, 1171.25, 1230].

Fig. 2.54 Visualizing Percentiles for Example 2.47.

Now, let’s generate a boxplot for the provided data.

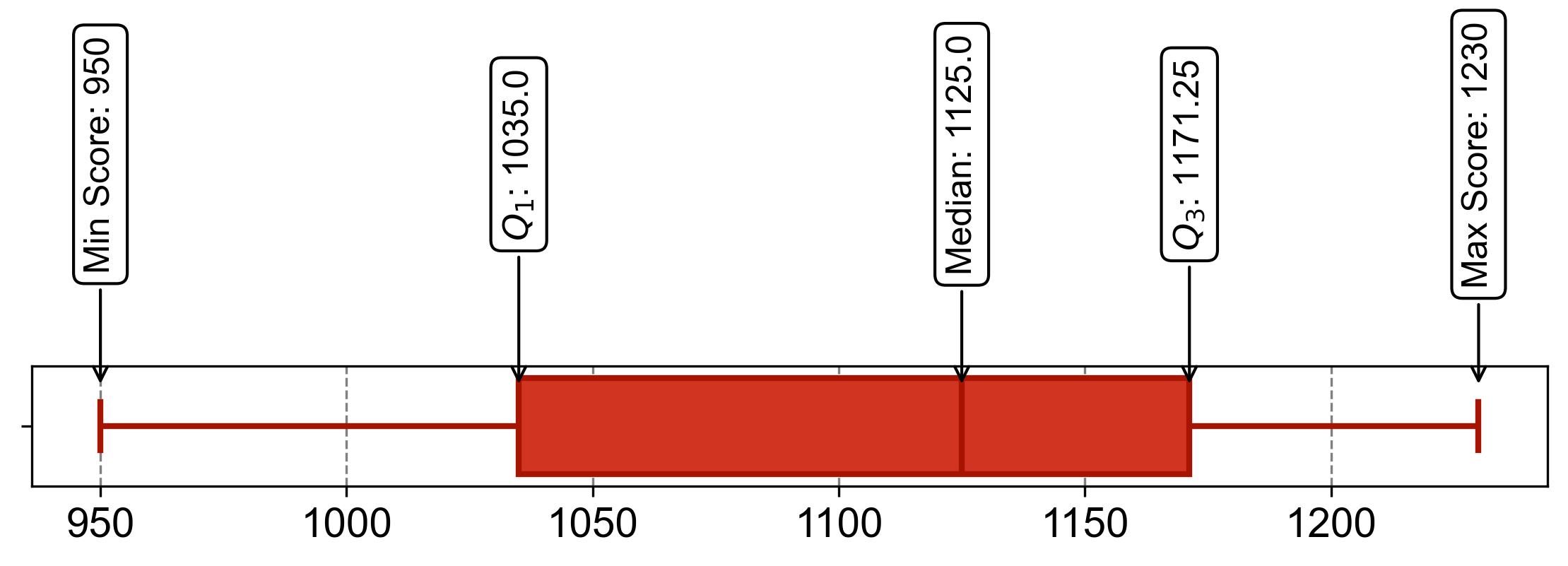
Fig. 2.55 Visualizing boxplot for Example 2.47.

Example 2.48

Imagine we have collected data on the number of books read by 10 students during their summer break:

12, 7, 9, 15, 8, 10, 11, 14, 13, 8

The task is to determine the 5-number summary of this dataset and then create a boxplot to visually depict the reading habits of the students.

Solution: To determine the 5-number summary for the given dataset representing the number of books read by 10 students during their summer break, we need to find the minimum, first quartile (\(Q_1\)), median (\(Q_2\)), third quartile (\(Q_3\)), and maximum values.

1. Organize the Data:

   • The number of books read by the 10 students are:

Index	1	2	3	4	5	6	7	8	9	10
Number	7	8	8	9	10	11	12	13	14	15

2. Calculate the Quartiles:

   • Using the formula:

     \[\begin{equation*}I = \dfrac{(10 - 1) \times q}{100} + 1\end{equation*}\]

   • For \(Q_1\) (25th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(10 - 1) \times 25}{100} + 1 = 3.25\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_1 = P_{25} = 8 + 0.25 \times (9 - 8) = 8 + 0.25 \times 1 = 8.25\end{equation*}\]

   • For \(Q_2\) (50th percentile, Median):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(10 - 1) \times 50}{100} + 1 = 5.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_2 = P_{50} = 10 + 0.5 \times (11 - 10) = 10 + 0.5 \times 1 = 10.5\end{equation*}\]

   • For \(Q_3\) (75th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(10 - 1) \times 75}{100} + 1 = 7.75\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_3 = P_{75} = 12 + 0.75 \times (13 - 12) = 12 + 0.75 \times 1 = 12.75\end{equation*}\]

3. Calculate the Minimum and Maximum:

   • Minimum: 7

   • Maximum: 15

The 5-number summary for the given dataset is: [7, 8.25, 10.5, 12.75, 15].

Fig. 2.56 Visualizing Percentiles for Example 2.48.

Now, let’s create a boxplot to visually depict the reading habits of the students.

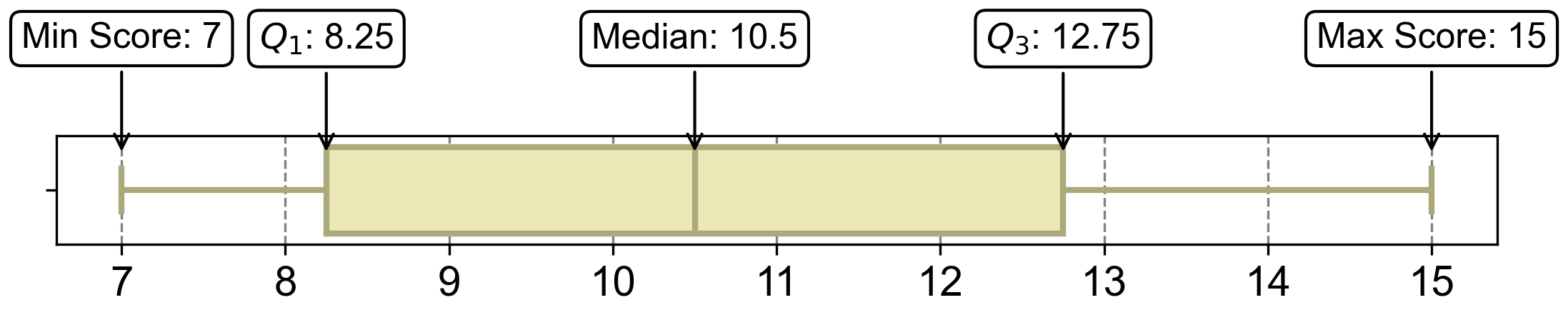
Fig. 2.57 Visualizing boxplot for Example 2.48.

2.7.4. Identifying Outliers for Modified Boxplots

A box plot, also known as a box-and-whisker diagram, is a graphical tool that visually depicts the distribution of a dataset. Here are the key components of a box plot:

1. Minimum Score:

   • This represents the smallest value in the dataset, excluding (potential) outliers.

   • It is represented by the left whisker’s end.

2. Lower Quartile (\(Q_1\)):

   • \(Q_1\) is the value below which 25% of the data falls, also known as the first quartile.

   • To find \(Q_1\):

     • Arrange the data in ascending order.

     • Find the median of the lower half of the data.

3. Median (\(Q_2\)):

   • \(Q_2\) is the middle value of the dataset, also referred to as the second quartile.

   • Half of the data points are equal to or greater than this value, and the other half are less.

4. Upper Quartile (\(Q_3\)):

   • \(Q_3\) is the value below which 75% of the data falls, also known as the third quartile.

   • To find \(Q_3\):

     • Arrange the data in ascending order.

     • Find the median of the upper half of the data.

5. Maximum Score:

   • This represents the largest value in the dataset, excluding (potential) outliers.

   • It is represented by the right whisker’s end.

6. Whiskers:

   • The whiskers extend from the box and indicate variability outside the upper and lower quartiles.

   • They capture the data within the interquartile range (IQR).

7. Interquartile Range (IQR):

   • The IQR is the range between \(Q_1\) and \(Q_3\): \begin{equation} \text{IQR} = Q_3 - Q_1 \end{equation}

Identifying Outliers

In a modified boxplot, a data value is considered an outlier if:

• It is above \(Q_3\) by an amount greater than \(1.5 \times \text{IQR}\).

• It is below \(Q_1\) by an amount less than \(1.5 \times \text{IQR}\).

Lower and Upper Limits

The lower limit and upper limit of a dataset are defined as follows:

• Lower Limit:

(2.18)\[\begin{equation} \text{Lower limit} = Q_1 - 1.5 \times \text{IQR} \end{equation}\]

• Upper Limit:

(2.19)\[\begin{equation} \text{Upper limit} = Q_3 + 1.5 \times \text{IQR} \end{equation}\]

• Any sample value below \(Q_1 - 1.5 \times \text{IQR}\) or exceeding \(Q_3 + 1.5 \times \text{IQR}\) is considered an outlier.

Fig. 2.58 Components of a boxplot (including potential outliers).

Note

In statistics, extreme observations, also known as outliers, are data points that significantly differ from the majority of the other data points in a dataset. Outliers can have a substantial impact on statistical analyses, leading to skewed results and affecting the overall interpretation of the data. Identifying and handling extreme observations appropriately is essential to ensure the validity and reliability of statistical analyses

Example 2.49

Suppose we have collected data on the speed (in km/h) of 15 different cars as they were tested on a track:

152, 147, 153, 135, 142, 155, 160, 130, 145, 158, 165, 138, 150, 156, 180

The task is to create a modified boxplot for this dataset.

Hint: You should identify the interquartile range (IQR), calculate the 1.5 * IQR rule to determine potential outliers, and then draw a boxplot that clearly marks these outliers.

Solution: To construct a modified boxplot for the dataset representing the speed (in km/h) of 15 different cars tested on a track, the following steps are undertaken:

Sorting the data yields:

Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Number	130	135	138	142	145	147	150	152	153	155	156	158	160	165	180

1. Quartiles and Interquartile Range (IQR) Computation:

   • For \(Q_1\) (25th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(15 - 1) \times 25}{100} + 1 = 4.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_1 = 142 + 0.5 \times (145 - 142) = 142 + 0.5 \times 3 = 143.5\end{equation*}\]

   • For \(Q_2\) (50th percentile, Median):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(15 - 1) \times 50}{100} + 1 = 8.0\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_2 = 152 + 0.0 \times (152 - 152) = 152 + 0.0 \times 0 = 152.0\end{equation*}\]

   • For \(Q_3\) (75th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(15 - 1) \times 75}{100} + 1 = 11.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_3 = 156 + 0.5 \times (158 - 156) = 156 + 0.5 \times 2 = 157.0\end{equation*}\]

   • The Interquartile Range (IQR) is computed as \(Q_3 - Q_1 = 157.0 - 143.5 = 13.5\).

2. Identification of Potential Outliers:

   • The lower bound is calculated as

   \[Q_1 - 1.5 \times IQR = 143.5 - 1.5 \times 13.5 = 123.25.\]

   • The upper bound is calculated as

   \[Q_3 + 1.5 \times IQR = 157.0 + 1.5 \times 13.5 = 177.25.\]

   • Any data point falling below the lower bound or exceeding the upper bound is identified as a potential outlier.

3. Construction of the Modified Boxplot:

   • A box is drawn from \(Q_1\) to \(Q_3\), with a line representing the median (\(Q_2\)).

   • “Whiskers” extend from \(Q_1\) to the lowest non-outlier and from \(Q_3\) to the highest non-outlier.

   • Outliers are marked as individual points.

Now, the process proceeds to construct the modified boxplot.

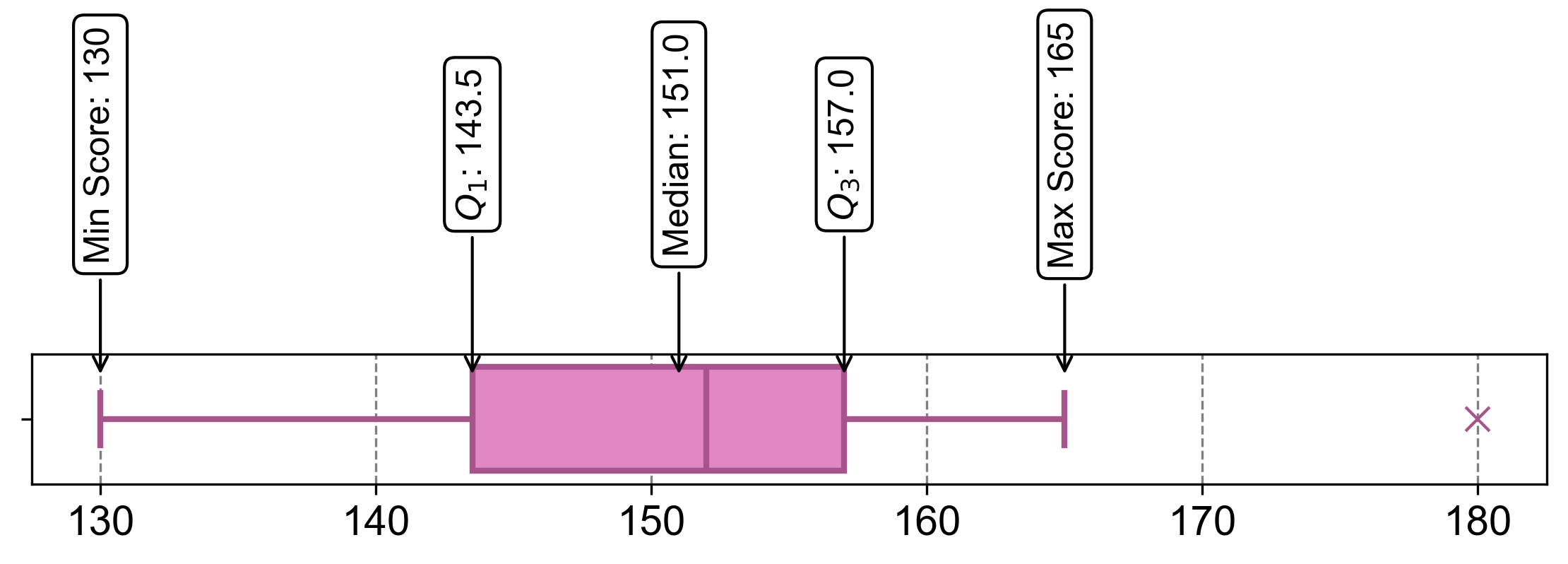
Fig. 2.59 Visualizing boxplot for Example 2.49.

Example 2.50

Suppose we have gathered data on the battery life (in hours) of 10 different models of smartphones during continuous use:

3, 10, 8, 12, 9, 11, 13, 7, 14, 10, 9

The task is to calculate the 5-number summary for this dataset and then construct a modified boxplot that takes into account any potential outliers.

Solution: To determine the 5-number summary for the dataset representing the battery life (in hours) of 10 different models of smartphones during continuous use, and to construct a modified boxplot, the following steps are taken:

Sorting the data results in:

Index	1	2	3	4	5	6	7	8	9	10	11
Number	3	7	8	9	9	10	10	11	12	13	14

1. Quartiles and Interquartile Range (IQR) Calculation:

   • For \(Q_1\) (25th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(11 - 1) \times 25}{100} + 1 = 3.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_1 = 8 + 0.5 \times (9 - 8) = 8 + 0.5 \times 1 = 8.5\end{equation*}\]

   • For \(Q_2\) (50th percentile, Median):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(11 - 1) \times 50}{100} + 1 = 6.0\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_2 = 10 + 0.0 \times (10 - 10) = 10 + 0.0 \times 0 = 10.0\end{equation*}\]

   • For \(Q_3\) (75th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(11 - 1) \times 75}{100} + 1 = 8.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_3 = 11 + 0.5 \times (12 - 11) = 11 + 0.5 \times 1 = 11.5\end{equation*}\]

   • The Interquartile Range (IQR) is computed as \(Q_3 - Q_1 = 11.5 - 8.5 = 3.0\).

2. Identification of Potential Outliers:

   • The lower bound is calculated as

   \[Q_1 - 1.5 \times IQR = 8.5 - 1.5 \times 3 = 4.0.\]

   • The upper bound is calculated as

   \[Q_3 + 1.5 \times IQR = 11.5 + 1.5 \times 3 = 16.0.\]

   • Any data point falling below the lower bound or exceeding the upper bound is considered a potential outlier.

3. Construction of the Modified Boxplot:

   • A box is drawn from \(Q_1\) to \(Q_3\), with a line representing the median (\(Q_2\)).

   • “Whiskers” extend from \(Q_1\) to the lowest non-outlier and from \(Q_3\) to the highest non-outlier.

   • Outliers are marked as individual points.

Now, the process proceeds to construct the modified boxplot.

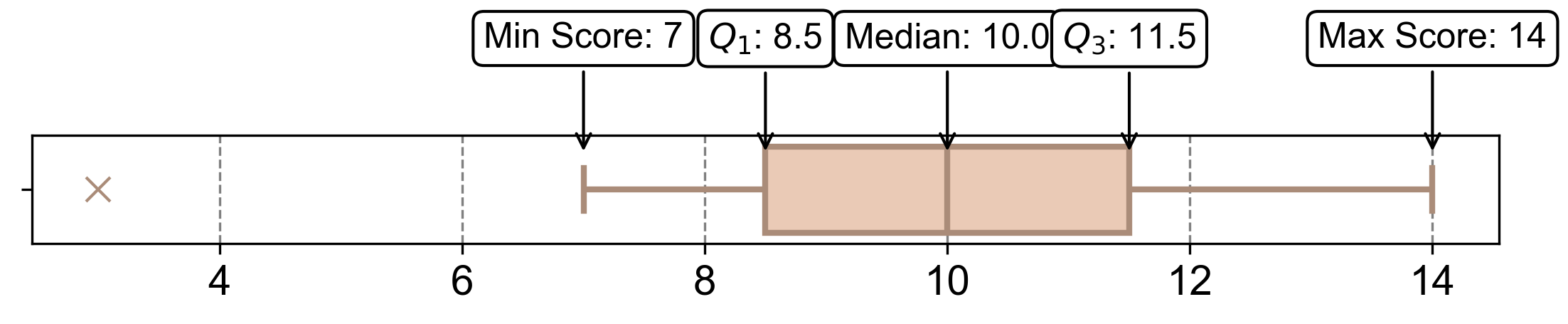
Fig. 2.60 Visualizing boxplot for Example 2.50.

Example 2.51

Imagine we have a dataset representing the daily production output (in units) of a factory over the past 10 working days:

265, 320, 335, 340, 295, 310, 300, 315, 305, 325, 290, 312, 318, 360

The task is to calculate the 5-number summary for this dataset and then create a boxplot, including identifying any potential outliers.

Solution: To determine the 5-number summary for the dataset representing the daily production output (in units) of a factory over the past 10 working days and to create a boxplot, while identifying any potential outliers, the following steps are followed:

Sorting the data yields:

Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Number	265	290	295	300	305	310	312	315	318	320	325	335	340	360

1. Quartiles and Interquartile Range (IQR) Calculation:

   • For \(Q_1\) (25th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(14 - 1) \times 25}{100} + 1 = 4.25\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_1 = 300 + 0.25 \times (305 - 300) = 300 + 0.25 \times 5 = 301.25\end{equation*}\]

   • For \(Q_2\) (50th percentile, Median):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(14 - 1) \times 50}{100} + 1 = 7.5\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_2 = 312 + 0.5 \times (315 - 312) = 312 + 0.5 \times 3 = 313.5\end{equation*}\]

   • For \(Q_3\) (75th percentile):

     • Calculate the index:

       \[\begin{equation*}I = \dfrac{(14 - 1) \times 75}{100} + 1 = 10.75\end{equation*}\]

     • Interpolate:

       \[\begin{equation*}Q_3 = 320 + 0.75 \times (325 - 320) = 320 + 0.75 \times 5 = 323.75\end{equation*}\]

   • The Interquartile Range (IQR) is computed as \(Q_3 - Q_1 = 323.75 - 301.25 = 22.5\).

2. Identification of Potential Outliers:

   • The lower bound is calculated as

\[Q_1 - 1.5 \times IQR = 301.25 - 1.5 \times 22.5 = 267.50.\]

• The upper bound is calculated as

\[Q_3 + 1.5 \times IQR = 323.75 + 1.5 \times 22.5 = 357.50.\]

• Any data point falling below the lower bound or exceeding the upper bound is considered a potential outlier.

1. Construction of the Boxplot:

   • A box is drawn from \(Q_1\) to \(Q_3\), with a line representing the median (\(Q_2\)).

   • “Whiskers” extend from \(Q_1\) to the lowest non-outlier and from \(Q_3\) to the highest non-outlier.

   • Outliers are marked as individual points.

Now, the process proceeds to create the boxplot.

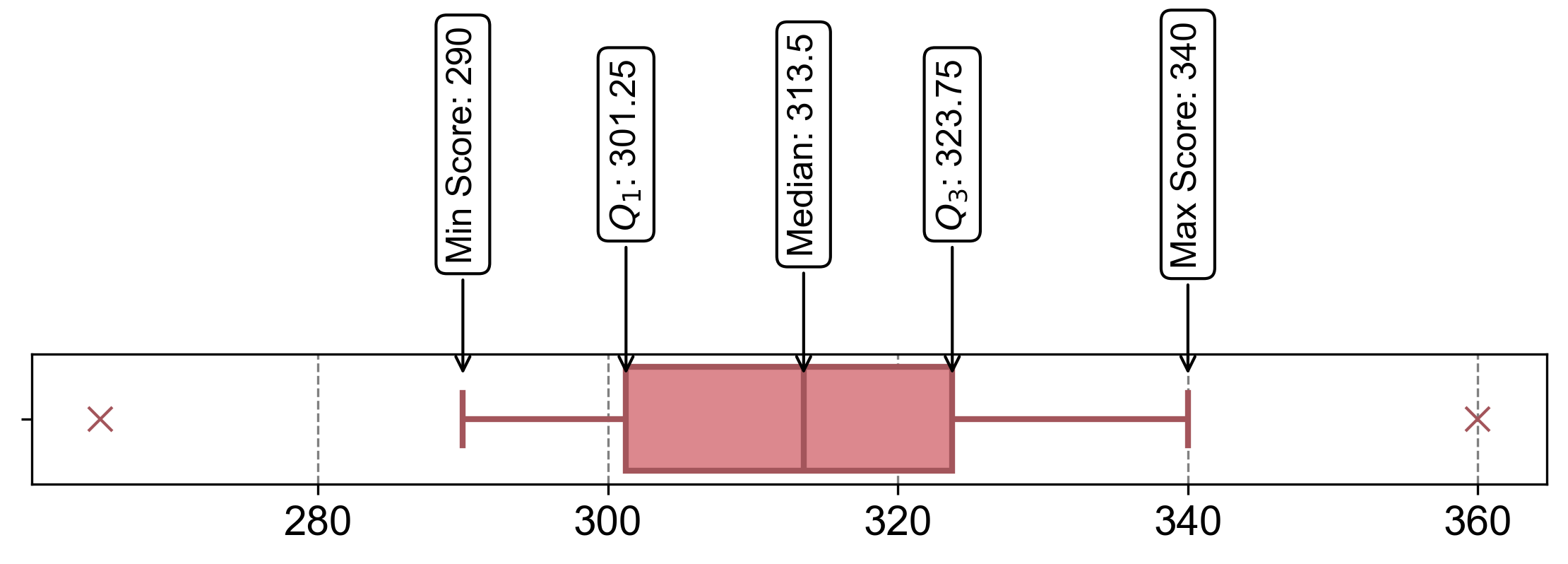
Fig. 2.61 Visualizing boxplot for Example 2.51.