2.6. Understanding Percentiles

Percentiles are a statistical measure that helps us understand how a particular value compares to the rest of the data in a dataset. They are particularly useful when we want to know the relative standing of a value within a group.

Imagine a classroom full of students lined up from shortest to tallest.

• Percentile tells us where a particular student falls in this line-up compared to others.

• Let’s say there are 20 students.

• The 50th percentile is the height of the student exactly in the middle. Half the class (10 students) will be shorter and the other half (10 students) will be taller.

• Someone at the 90th percentile is very tall. Only 2 students out of 20 will be taller than this student.

• The 10th percentile is on the shorter side. There will be 18 students taller than this student.

2.6.1. Key Points about Percentiles

• Dividing the Data: Percentiles split the data into 100 groups of equal size. Each group represents approximately 1% of the data points.

• Not a Percentage Score: Being in the 90th percentile does not mean you scored 90 out of 100. It means you scored higher than 90% of the other values in the dataset.

• Relative Standing: Percentiles tell us about the position of a value relative to others, not its absolute value.

2.6.2. Calculating Percentiles

To find the value below which a certain percentage of observations fall, you can calculate the percentile using the following steps [Hyndman and Fan, 1996]:

1. Organize the Data:

   • Begin by sorting all the data points in your dataset in ascending order.

2. Find the Index:

   • The index determines where the percentile value lies within your sorted data. To find the index for the \(q\)-th percentile (where \( q \) is the desired percentile), use the formula:

   (2.14)\[I = (N - 1) \times \dfrac{q}{100} +1\]

   Here, \( N \) represents the total number of observations in your dataset.

3. Identify the Percentile Value:

   • If the index \( I \) is a whole number, the percentile value is the observation at that index in your sorted list.

   • If the index \( I \) is not a whole number, you’ll need to interpolate to find the percentile value. This means you’ll calculate the value that lies at the fractional part of the index between two observations. The formula for linear interpolation is:

   (2.15)\[ P = V_i + (V_{i+1} - V_i) \times (I - i), \quad i\geq 1\]

   In this formula, \( P \) is the percentile value you’re calculating, \( V_i \) is the value at the integer part of the index \( I \), and \( V_{i+1} \) is the next value in the sorted list. The term \( (I - i) \) represents the fractional part of the index.

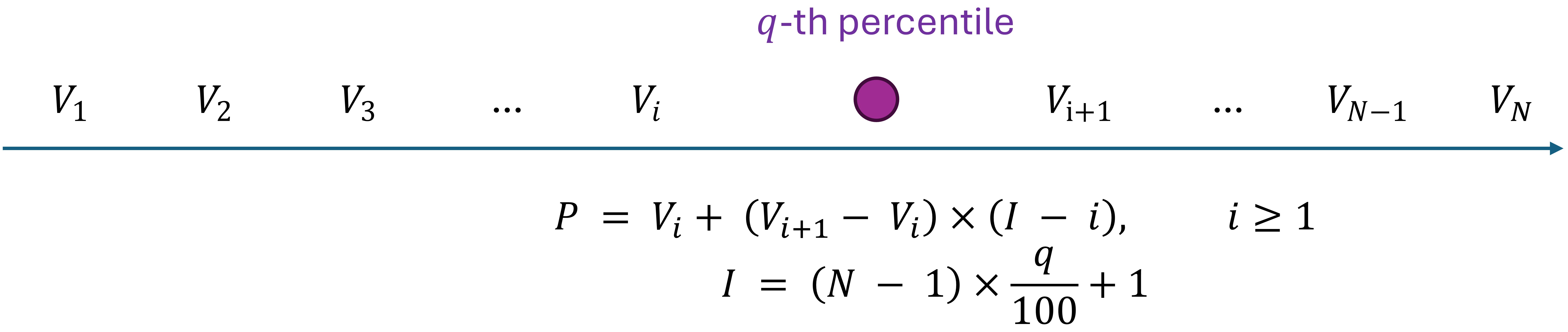
Fig. 2.31 Calculating the q-th Percentile: This image also illustrates how to find the q-th percentile in a dataset. The formula is: \(P = V_i + (V_{i+1} - V_i) \times (I - i)\) where \(I = (N - 1) \times \dfrac {q}{100} +1\) and \(i \geq 1\). The number line shows the variables \(V_1\), \(V_2\), \(V_3\), \(\ldots\), \(V_i\), \(V_{i+1}\), \(\ldots\), \(V_{N-1}\), \(V_{N}\) with the q-th percentile marked between \(V_i\) and \(V_{i+1}\).

Remark

We could also start the index from 0, 1, 2, …, and in that case, (2.14) and (2.15) can be expressed as follows:

(2.16)\[\begin{equation} \begin{cases} I &= (N - 1) \times \dfrac{q}{100}, \\ &\\ P &= V_i + (V_{i+1} - V_i) \times (I - i), \quad i\geq 0 \end{cases} \end{equation}\]

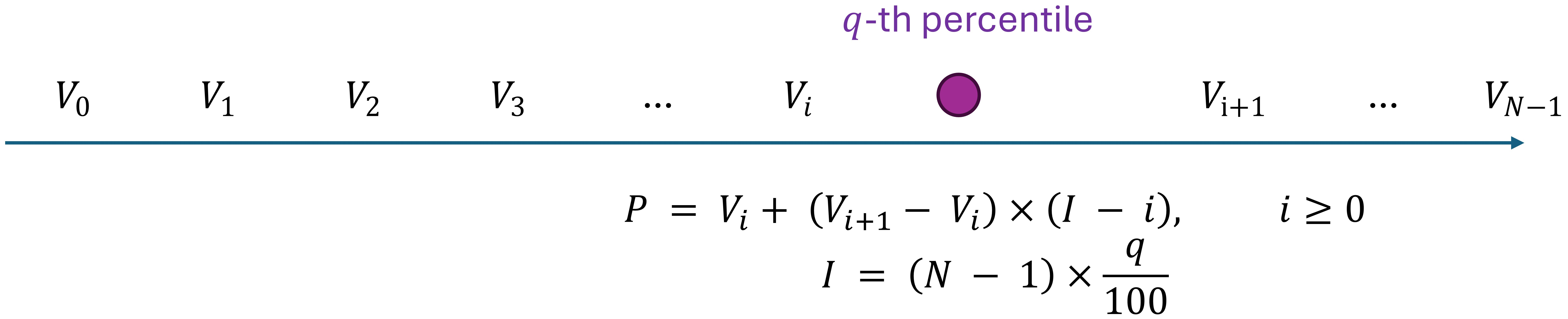
Fig. 2.32 Finding the q-th Percentile: This image illustrates how to calculate the q-th percentile in a dataset. The formula is: \(P = V_i + (V_{i+1} - V_i) \times (I - i)\) where \(I = (N - 1) \times \dfrac{q}{100} + 1\) and \(i \geq 0\). The number line shows the variables \(V_0\), \(V_1\), \(V_2\), \(V_3\), \(\ldots\), \(V_i\), \(V_{i+1}\), \(\ldots\), \(V_{N-1}\) with the q-th percentile marked above it.

2.6.3. Quartiles

Quartiles divide a dataset into four equal-sized groups. Each group contains approximately 25% of the values from the data. These measures help us examine relative positions within the dataset. Here’s what you need to know:

• Three Quartiles: Denoted as \(Q_1\), \(Q_2\), and \(Q_3\).

  • \(Q_1\): The value below which 25% of the data falls.

  • \(Q_2\) (Median): The value below which 50% of the data falls.

  • \(Q_3\): The value below which 75% of the data falls.

Note

When identifying percentiles such as \(P_{25}\), \(P_{50}\), or \(P_{75}\), we directly find the quartiles \(Q_1\), \(Q_2\), or \(Q_3\) instead.

Example 2.36

You are given the following heights (in centimeters) of 10 individuals:

150, 160, 165, 170, 175, 180, 185, 190, 195, 200

Find the 30th, 40th, 50th, 70th, and 65th percentiles.

Solution: We’ll use the formula for linear interpolation between data points to calculate the percentiles mathematically for the given data. The data points are already sorted, which is the first step. The data set is:

Index	1	2	3	4	5	6	7	8	9	10
Number	150	160	165	170	175	180	185	190	195	200

There are \( N = 10 \) data points. Let’s calculate the percentiles one by one.

30th Percentile (\(P_{30}\)):

1. Calculate the index:

\[\begin{equation*}I = \dfrac{(10 - 1) \times 30}{100} + 1 = 3.7\end{equation*}\]

2. Since the index is not an integer, we interpolate between the 3rd and 4th values in the sorted list (165 and 170).

3. Linear interpolation:

\[\begin{equation*}P_{30} = 165 + (170 - 165) \times (3.7 - 3) = 165 + 5 \times 0.7 = 168.5\end{equation*}\]

Fig. 2.33 Visualizing Percentiles for 30th Percentile (\(P_{30}\)).

40th Percentile (\(P_{40}\)):

1. Calculate the index:

\[\begin{equation*}I = \dfrac{(10 - 1) \times 40}{100} + 1 = 4.6\end{equation*}\]

2. Interpolate between the 4th and 5th values (170 and 175).

3. Linear interpolation:

\[\begin{equation*}P_{40} = 170 + (175 - 170) \times (4.6 - 4) = 170 + 5 \times 0.6 = 173.0\end{equation*}\]

Fig. 2.34 Visualizing Percentiles for 40th Percentile (\(P_{40}\)).

50th Percentile (\(P_{50}\)) or Median:

1. Calculate the index:

\[\begin{equation*}I = \dfrac{(10 - 1) \times 50}{100} + 1 = 5.5\end{equation*}\]

2. Interpolate between the 5th and 6th values (175 and 180).

3. Linear interpolation:

\[\begin{equation*}P_{50} = 175 + (180 - 175) \times (5.5 - 5) = 175 + 5 \times 0.5 = 177.5\end{equation*}\]

Fig. 2.35 Visualizing Percentiles for 50th Percentile (\(P_{50}\)) or Median.

70th Percentile (\(P_{70}\)):

1. Calculate the index:

\[\begin{equation*}I = \dfrac{(10 - 1) \times 70}{100} + 1 = 7.3\end{equation*}\]

2. Interpolate between the 7th and 8th values (185 and 190).

3. Linear interpolation:

\[\begin{equation*}P_{70} = 185 + (190 - 185) \times (7.3 - 7) = 185 + 5 \times 0.3 = 186.5\end{equation*}\]

Fig. 2.36 Visualizing Percentiles for 70th Percentile (\(P_{70}\)).

65th Percentile (\(P_{65}\)):

1. Calculate the index:

\[\begin{equation*}I = \dfrac{(10 - 1) \times 65}{100} + 1 = 6.85\end{equation*}\]

2. Interpolate between the 6th and 7th values (180 and 185).

3. Linear interpolation:

\[\begin{equation*}P_{65} = 180 + (185 - 180) \times (6.85 - 6) = 180 + 5 \times 0.85 = 184.25\end{equation*}\]

Fig. 2.37 Visualizing Percentiles for 65th Percentile (\(P_{65}\)).

Example 2.37

Find the percentiles for the given ages of Academy Award-winning best actors:

18, 21, 22, 25, 26, 27, 29, 30, 31, 33, 36, 37, 41, 42, 47, 52, 55, 57, 58, 62, 64, 67, 69, 71, 72, 73, 74, 76, 77

• a. 40th Percentile

• b. 78th Percentile

Solution:

The ordered ages are:

Index	1	2	3	4	5	6	7	8	9	10
Number	18	21	22	25	26	27	29	30	31	33
Index	11	12	13	14	15	16	17	18	19	20
Number	36	37	41	42	47	52	55	57	58	62
Index	21	22	23	24	25	26	27	28	29
Number	64	67	69	71	72	73	74	76	77

a. 40th Percentile:

1. Organize the Data:

   • The ordered ages are: 18, 21, 22, 25, 26, 27, 29, 30, 31, 33, 36, 37, 41, 42, 47, 52, 55, 57, 58, 62, 64, 67, 69, 71, 72, 73, 74, 76, 77.

2. Find the Index:

   • Using the formula:

     \[\begin{equation*} I = \dfrac{(29 - 1) \times 40}{100} + 1 = 12.2 \end{equation*}\]

     This gives us the index.

3. Identify the Percentile Value:

   • Since the index is not a whole number, we interpolate:

     \[\begin{equation*} P_{40} = 37 + 0.2 \times (41 - 37) = 37 + 0.2 \times 4 = 37.8 \end{equation*}\]

Fig. 2.38 Visualizing Percentiles for 40th Percentile (\(P_{40}\)).

b. 78th Percentile:

1. Organize the Data:

   • The ordered ages are the same as before.

2. Find the Index:

   • Using the formula:

     \[\begin{equation*} I = \dfrac{(29 - 1) \times 78}{100} + 1 = 22.84 \end{equation*}\]

     This gives us the index.

3. Identify the Percentile Value:

   • Since the index is not a whole number, we interpolate:

     \[\begin{equation*} P_{78} = 67 + 0.84 \times (69 - 67) = 67 + 0.84 \times 2 = 68.68 \end{equation*}\]

   Therefore, the 78th percentile is 68.68.

Fig. 2.39 Visualizing Percentiles for 78th Percentile (\(P_{78}\)).

Example 2.38

Suppose you have the following test scores (ordered from lowest to highest):

43, 54, 56, 61, 62, 66, 68, 69, 69, 70, 71, 72, 77, 78, 79, 85, 87, 88, 89, 93, 95, 96, 98, 99, 99.

Find the 20th, 40th, 60th, 80th, and 90th percentiles.

Solution:

Index	1	2	3	4	5	6	7	8	9	10	11	12	13
Number	43	54	56	61	62	66	68	69	69	70	71	72	77
Index	14	15	16	17	18	19	20	21	22	23	24	25
Number	78	79	85	87	88	89	93	95	96	98	99	99

1. For the 20th percentile (\(P_{20}\)):

• Calculate the index:

\[\begin{equation*}I = \dfrac{(25 - 1) \times 20}{100} + 1 = 5.8\end{equation*}\]

• Interpolate:

\[\begin{equation*}P_{20} = 62 + 0.8 \times (66 - 62) = 62 + 0.8 \times 4 = 65.2\end{equation*}\]

Fig. 2.40 Visualizing Percentiles for 20th Percentile (\(P_{20}\)).

2. For the 40th percentile (\(P_{40}\)):

• Calculate the index:

\[\begin{equation*}I = \dfrac{(25 - 1) \times 40}{100} + 1 = 10.6\end{equation*}\]

• Interpolate:

\[\begin{equation*}P_{40} = 70 + 0.6 \times (71 - 70) = 70 + 0.6 \times 1 = 70.6\end{equation*}\]

Fig. 2.41 Visualizing Percentiles for 40th Percentile (\(P_{40}\)).

3. For the 60th percentile (\(P_{60}\)):

• Calculate the index:

  \[\begin{equation*}I = \dfrac{(25 - 1) \times 60}{100} + 1 = 15.4\end{equation*}\]

• Interpolate:

\[\begin{equation*}P_{60} = 79 + 0.4 \times (85 - 79) = 79 + 0.4 \times 6 = 81.4\end{equation*}\]

Fig. 2.42 Visualizing Percentiles for 60th Percentile (\(P_{60}\)).

4. For the 80th percentile (\(P_{80}\)):

• Calculate the index:

\[\begin{equation*}I = \dfrac{(25 - 1) \times 80}{100} + 1 = 20.2\end{equation*}\]

• Interpolate:

\[\begin{equation*}P_{80} = 93 + 0.2 \times (95 - 93) = 93 + 0.2 \times 2 = 93.4\end{equation*}\]

Fig. 2.43 Visualizing Percentiles for 80th Percentile (\(P_{80}\)).

5. For the 90th percentile (\(P_{90}\)):

• Calculate the index:

\[\begin{equation*}I = \dfrac{(25 - 1) \times 90}{100} + 1 = 22.6\end{equation*}\]

• Interpolate:

\[\begin{equation*}P_{90} = 96 + 0.6 \times (98 - 96) = 96 + 0.6 \times 2 = 97.2\end{equation*}\]

Fig. 2.44 Visualizing Percentiles for 90th Percentile (\(P_{90}\)).

Example 2.39

Find the requested percentiles for the given dataset of ages:

36.0, 37.0, 40.0, 40.0, 41.0, 43.0, 43.5, 46.0, 46.0, 47.0, 48.0, 48.0, 49.0, 50.0, 52.0, 52.5, 53.0, 53.0, 54.0, 57.3, 57.5, 58.0, 59.0, 59.0, 59.0, 60.0, 60.5, 61.0, 61.0, 61.5, 62.0, 63.0, 63.0, 63.0, 63.5, 64.0, 64.0, 64.0, 65.0, 65.0, 66.5, 67.0, 67.5, 68.5, 70.0, 70.5, 72.0, 72.0, 72.0, 72.0, 73.0, 73.5, 75.0, 76.5

• a. \(P_{60}\) (60th Percentile)

• b. \(P_{40}\) (40th Percentile)

• c. \(P_{50}\) (50th Percentile, Median)

• d. \(P_{25}\) (25th Percentile, \(Q_{1}\))

Solution:

Organize the Data:

Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Number	36	37	40	40	41	43	43.5	46	46	47	48	48	49	50
Index	15	16	17	18	19	20	21	22	23	24	25	26	27	28
Number	52	52.5	53	53	54	57.3	57.5	58	59	59	59	60	60.5	61
Index	29	30	31	32	33	34	35	36	37	38	39	40	41	42
Number	61	61.5	62	63	63	63	63.5	64	64	64	65	65	66.5	67
Index	43	44	45	46	47	48	49	50	51	52	53	54
Number	67.5	68.5	70	70.5	72	72	72	72	73	73.5	75	76.5

• For \(P_{60}\):

  • Calculate the index:

\[\begin{equation*}I = \dfrac{(58 - 1) \times 60}{100} + 1 = 32.8\end{equation*}\]

• Interpolate:

\[\begin{equation*}P_{60} = 63.0 + 0.8 \times (63.0 - 63.0) = 63.0 + 0.8 \times 0.0 = 63.0\end{equation*}\]

• For \(P_{40}\):

  • Calculate the index:

\[\begin{equation*}I = \dfrac{(58 - 1) \times 40}{100} + 1 = 22.2\end{equation*}\]

• Interpolate:

\[\begin{equation*}P_{40} = 58.0 + 0.2 \times (59.0 - 58.0) = 58.0 + 0.2 \times 1.0 = 58.2\end{equation*}\]

• For \(P_{50}\) (Median):

  • Calculate the index:

\[\begin{equation*}I = \dfrac{(58 - 1) \times 50}{100} + 1 = 27.5\end{equation*}\]

• Interpolate:

\[\begin{equation*}P_{50} = 60.5 + 0.5 \times (61.0 - 60.5) = 60.5 + 0.5 \times 0.5 = 60.75\end{equation*}\]

• For \(P_{25}\) (Q1):

  • Calculate the index:

\[\begin{equation*}I = \dfrac{(58 - 1) \times 25}{100} + 1 = 14.25\end{equation*}\]

• Interpolate:

\[\begin{equation*}P_{25} = 50.0 + 0.25 \times (52.0 - 50.0) = 50.0 + 0.25 \times 2.0 = 50.5\end{equation*}\]

Therefore, the calculated percentiles are:

\[\begin{equation*}P_{60} = 63.00, \, P_{40} = 58.20, \, P_{50} = 60.75, \, \text{and} \, P_{25} = 50.50\end{equation*}\]

2.6.4. Finding the Percentile of a Data Value

1. Count the Values Less Than \(x\):

   • Determine how many values in your dataset are less than the given value \(x\). Let’s call this count \(n\).

2. Calculate the Percentile:

   • Divide \(n\) by the total number of values in the dataset. Let’s call the total number of values \(N\).

   • Multiply the result by 100.

   • The formula can be expressed as:

   (2.17)\[\begin{equation}\text{Percentile} = \dfrac{n}{N} \times 100\end{equation}\]

3. Rounding:

   • Depending on the required precision, you may round the result to a certain number of decimal places or to the nearest whole number.

Remark

Some textbooks and statistical software may use different definitions for calculating percentiles, specifically:

• “Less than or equal to” (≤): Counts values that are equal to the target value.

• “Strictly less than” (<): Counts only those values that are less than the target value.

Impact on Results: These variations can lead to different percentile values, particularly in the following scenarios:

• Small Datasets: The choice of method can significantly affect the results.

• Repeated Values: The handling of duplicate values can also influence the calculated percentiles.

Importance of Context: Always check the specific definition used in your context, as it is essential for accurate interpretation and comparison of percentile results across different sources or statistical tools.

Example 2.40

Find the requested percentiles for the given dataset of ages:

Dataset (ordered from smallest to largest):

18, 18, 21, 22, 25, 26, 27, 29, 30, 31, 31, 33, 36, 37, 37, 41, 42, 47, 52, 55, 57, 58, 62, 64, 67, 69, 71, 72, 73, 74, 76, 77

• a. Percentile of 37

• b. Percentile of 72

Solution:

Index	1	2	3	4	5	6	7	8	9	10	11
Number	18	18	21	22	25	26	27	29	30	31	31
Index	12	13	14	15	16	17	18	19	20	21	22
Number	33	36	37	37	41	42	47	52	55	57	58
Index	23	24	25	26	27	28	29	30	31	32
Number	62	64	67	69	71	72	73	74	76	77

a. Percentile of 37:

• Count the number of values less than 37:

• There are 15 values less than or equal to 37.

• Divide this by the total number of values (\(n = 32\)): \(\dfrac{{15}}{{32}} \times 100 = 46.88\%\).

• Therefore, the percentile of 37.0 inches is approximately 47%.

b. Percentile of 72:

• Count the number of values less than 72:

• There are 28 values less than or equal to 72.

• Divide this by the total number of values (\(n = 32\)): \(\dfrac{{28}}{{32}} \times 100 = 87.50\%\).

• Therefore, the percentile of 72.0 inches is approximately 88%.

Example 2.41

Find the percentiles corresponding to the given lengths:

Dataset (ordered from smallest to largest):

36.0, 37.0, 40.0, 40.0, 41.0, 43.0, 43.5, 46.0, 46.0, 47.0, 48.0, 48.0, 49.0, 50.0, 52.0, 52.5, 53.0, 53.0, 54.0, 57.3, 57.5, 58.0, 59.0, 59.0, 59.0, 60.0, 60.5, 61.0, 61.0, 61.5, 62.0, 63.0, 63.0, 63.0, 63.5, 64.0, 64.0, 64.0, 65.0, 65.0, 66.5, 67.0, 67.5, 68.5, 70.0, 70.5, 72.0, 72.0, 72.0, 72.0, 73.0, 73.5, 75.0, 76.5

• a. Percentile of 61.0 in

• b. Percentile of 47.0 in

• c. Percentile of 70.0 in

• d. Percentile of 58.0 in

Solution:

Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Number	36	37	40	40	41	43	43.5	46	46	47	48	48	49	50
Index	15	16	17	18	19	20	21	22	23	24	25	26	27	28
Number	52	52.5	53	53	54	57.3	57.5	58	59	59	59	60	60.5	61
Index	29	30	31	32	33	34	35	36	37	38	39	40	41	42
Number	61	61.5	62	63	63	63	63.5	64	64	64	65	65	66.5	67
Index	43	44	45	46	47	48	49	50	51	52	53	54
Number	67.5	68.5	70	70.5	72	72	72	72	73	73.5	75	76.5

a. Percentile of 61.0 in:

• Count the number of values less than 61.0:

• There are 29 values less than or equal to 61.0.

• Divide this by the total number of values (\(n = 54\)): \(\dfrac{{29}}{{54}} \times 100 = 53.70 \approx 54\%\).

• Therefore, the percentile of 61.0 inches is approximately 54%.

b. Percentile of 47.0 in:

• Count the number of values less than 47.0:

• There are 10 values less than or equal to 47.0.

• Divide this by the total number of values (\(n = 54\)): \(\dfrac{{10}}{{54}} \times 100 = 17.86 \approx 18\%\).

• Therefore, the percentile of 47.0 inches is approximately 18%.

c. Percentile of 70.0 in:

• Count the number of values less than 70.0:

• There are 45 values less than or equal to 70.0.

• Divide this by the total number of values (\(n = 54\)): \(\dfrac{{45}}{{54}} \times 100 = 80.36 \approx 83\%\).

• Therefore, the percentile of 70.0 inches is approximately 83%.

d. Percentile of 58.0 in:

• Count the number of values less than 58.0:

• There are 22 values less than or equal to 58.0.

• Divide this by the total number of values (\(n = 54\)): \(\dfrac{{22}}{{54}} \times 100 = 39.29 \approx 41\%\).

• Therefore, the percentile of 58.0 inches is approximately 41%.