7.5. QR factorization

Square matrix \(A\) can be decomposed as \(A=QR\) where \(Q\) is an orthogonal matrix (\(Q^{*}Q=QQ^{*}=I\)) and \(R\) is an upper triangular matrix. If \(A\) is invertible and \(R\) is positive, then the factorization is unique.

Furthermore, there are several methods for computing the \(QR\) decomposition such as the Gram–Schmidt process, and the Householder transformations, … Here, we use the Gram–Schmidt process.

Consider matrix \(A = \begin{bmatrix}| & | & & | \\ \vec{a}_1 & \vec{a}_2 & \dots & \vec{a}_n \\ | & | & & | \end{bmatrix}\) were \( \vec{a}_i\) are the columns of the full column rank matrix \(A\). Now, define the projection as follows:

\[\begin{align*} \operatorname{proj}_{\vec{u}}\vec{a} = \frac{ \left\langle \vec{u},~\vec{a} \right\rangle }{\left\langle \vec{u},~\vec{u}\right\rangle} \vec{u} \end{align*}\]

Therefore,

\[\begin{align*} \vec{u}_{1} & = \vec{a}_{1}, &\vec{e}_{1}& = \frac{\vec{u}_{1}}{\|\vec{u}_{1}\|},\\ \vec{u}_{2} & = \vec{a}_{2} - \operatorname{proj}_{\vec{u}_{1}}\,\vec{a}_{2},&\vec{e}_{2} &= \frac{\vec{u}_{2}}{\|\vec{u}_{2}\|},\\ \vec{u}_{3}&=\vec{a}_{3}-\operatorname {proj} _{\vec{u}_{1}}\,\vec{a}_{3}-\operatorname {proj} _{\vec{u}_{2}}\,\vec{a}_{3},&\vec{e}_{3}&= \frac{\vec{u}_{3}}{\|\vec{u}_{3}\|},\\ &\vdots & &\vdots \\ \vec{u}_{k}&=\vec{a}_{k}-\sum _{j=1}^{k-1}\operatorname {proj} _{\vec{u}_{j}}\,\vec{a}_{k},&\vec{e}_{k}&= \frac{\vec{u}_{k}}{\|\vec{u}_{k}\|}. \end{align*}\]

Now, \(\vec{a}_{i}\) can be expressed as

\[\begin{align*} \begin{cases} \vec{a}_{1}=\langle \vec{e}_{1},\vec{a}_{1}\rangle \vec{e}_{1}\\ \vec{a}_{2}=\langle \vec{e}_{1},\vec{a}_{2}\rangle \vec{e}_{1}+\langle \vec{e}_{2},\vec{a}_{2}\rangle \vec{e}_{2}\\ \vec{a}_{3}=\langle \vec{e}_{1},\vec{a}_{3}\rangle \vec{e}_{1}+\langle \vec{e}_{2},\vec{a}_{3}\rangle \vec{e}_{2}+\langle \vec{e}_{3},\vec{a}_{3}\rangle \vec{e}_{3}\\&\vdots \\ \vec{a}_{k}=\sum _{j=1}^{k}\langle \vec{e}_{j},\vec{a}_{k}\rangle \vec{e}_{j} \end{cases} \end{align*}\]

where \(\left\langle \vec{e}_{i},\vec{a}_{i}\right\rangle =\left\|\vec{u}_{i}\right\|\). This can be written in matrix form:

\[\begin{align*} A&=QR \end{align*}\]

\[\begin{align*} \begin{bmatrix}a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ a_{31} & a_{32} & \dots & a_{3n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn} \end{bmatrix} &= \begin{bmatrix}| & | & & | \\ \vec{e}_1 & \vec{e}_2 & \dots & \vec{e}_n\\ | & | & & | \end{bmatrix} \begin{bmatrix} \langle \vec{e}_{1},\vec{a}_{1}\rangle &\langle \vec{e}_{1},\vec{a}_{2}\rangle &\langle \vec{e}_{1},\vec{a}_{3}\rangle &\ldots & \langle \vec{e}_{1},\vec{a}_{n}\rangle \\ 0&\langle \vec{e}_{2},\vec{a}_{2}\rangle &\langle \vec{e}_{2},\vec{a}_{3}\rangle &\ldots & \langle \vec{e}_{2},\vec{a}_{n}\rangle\\ 0&0&\langle \vec{e}_{3},\vec{a}_{3}\rangle &\ldots & \langle \vec{e}_{3},\vec{a}_{n}\rangle\\ \vdots &\vdots &\vdots &\ddots &\vdots\\ 0 & 0 & \dots & \dots & \langle \vec{e}_{n},\vec{a}_{n} \rangle \end{bmatrix}. \end{align*}\]

See [Allaire, Kaber, Trabelsi, and Allaire, 2008, Khoury and Harder, 2016] for the full derivation of this algorithm.

Python Code

import numpy as np
import pandas as pd

def myQR(A):
    '''
    Square matrix $A$ can be decomposed as A=QR
    where Q is an orthogonal matrix and
    R is an upper triangular matrix.

    Parameters
    ----------
    A : numpy array
        DESCRIPTION. Matrix A

    Returns
    -------
    Q : numpy array
        DESCRIPTION. Matrix Q from A = QR
    R : numpy array
        DESCRIPTION. Matrix R from A = QR

    '''
    n = A.shape[0]
    Q = np.zeros([n,n], dtype = float)
    R = np.zeros([n,n], dtype = float)
    A = A.astype(float)
    for j in range(n):
        T = A[:, j]
        for i in range(j):
            R[i, j] = np.dot(Q[:, i], A[:, j])
            T -= R[i, j] * Q[:, i]
        R[j, j] = np.sqrt(np.dot(T, T))
        Q[:, j] = T /R[j, j]
        del T
    return Q, R

MATLAB Code

function [Q, R] = myQR(A)
%{
Square matrix $A$ can be decomposed as A=QR
where Q is an orthogonal matrix and
R is an upper triangular matrix.

Parameters
----------
A : numpy array
    DESCRIPTION. Matrix A

Returns
-------
Q : numpy array
    DESCRIPTION. Matrix Q from A = QR
R : numpy array
    DESCRIPTION. Matrix R from A = QR

%}
n=length(A);
Q =zeros(n,n);
R = zeros(n,n);
for j=1:n
    T = A(:, j);
    for i=1:j
        R(i, j) = dot(Q(:, i), A(:, j));
        T = T - R(i, j) * Q(:, i);
    end
    R(j, j) = sqrt(dot(T, T));
    Q(:, j) = T /R(j, j);
end

import sys
sys.path.insert(0,'..')
import hd_tools as hd

Loading BokehJS ...

Example: Apply QR decomposition on the following matrix and identify \(Q\) and \(R\).

\[\begin{align*}A = \left[\begin{array}{cccc} 7 & 3 & -1 & 2\\ 3 & 8 & 1 & -4\\ -1 & 1 & 4 & -1\\ 2 & -4 & -1 & 6 \end{array}\right].\end{align*}\]

Solution: We have,

import numpy as np
from hd_Matrix_Decomposition import myQR
from IPython.display import display, Latex
from sympy import init_session, init_printing, Matrix
A = np.array([ [7, 3, -1, 2], [3, 8, 1, -4], [-1, 1, 4, -1], [2, -4, -1, 6] ])
Q, R = myQR(A)
display(Latex(r'Q ='), Matrix(np.round(Q, 2)))
display(Latex(r'R ='), Matrix(np.round(R, 2)))
display(Latex(r'QR ='), Matrix(np.round(Q@R, 2)))
display(Latex(r'QQ^T ='), Matrix(np.round(Q@(Q.T), 2)))
display(Latex(r'Q^TQ ='), Matrix(np.round((Q.T)@Q, 2)))

\[Q =\]

\[\begin{split}\displaystyle \left[\begin{matrix}0.88 & -0.12 & 0.11 & -0.44\\0.38 & 0.75 & -0.06 & 0.53\\-0.13 & 0.19 & 0.97 & -0.06\\0.25 & -0.62 & 0.2 & 0.72\end{matrix}\right]\end{split}\]

\[R =\]

\[\begin{split}\displaystyle \left[\begin{matrix}7.94 & 4.54 & -1.26 & 1.89\\0 & 8.33 & 2.25 & -7.15\\0 & 0 & 3.52 & 0.69\\0 & 0 & 0 & 1.35\end{matrix}\right]\end{split}\]

\[QR =\]

\[\begin{split}\displaystyle \left[\begin{matrix}7.0 & 3.0 & -1.0 & 2.0\\3.0 & 8.0 & 1.0 & -4.0\\-1.0 & 1.0 & 4.0 & -1.0\\2.0 & -4.0 & -1.0 & 6.0\end{matrix}\right]\end{split}\]

\[QQ^T =\]

\[\begin{split}\displaystyle \left[\begin{matrix}1.0 & 0 & 0 & 0\\0 & 1.0 & 0 & 0\\0 & 0 & 1.0 & 0\\0 & 0 & 0 & 1.0\end{matrix}\right]\end{split}\]

\[Q^TQ =\]

\[\begin{split}\displaystyle \left[\begin{matrix}1.0 & 0 & 0 & 0\\0 & 1.0 & 0 & 0\\0 & 0 & 1.0 & 0\\0 & 0 & 0 & 1.0\end{matrix}\right]\end{split}\]

hd.matrix_decomp_fig(mats = [Q, R, np.round(Q@(Q.T), 1), np.round((Q.T)@Q, 1), np.round(np.matmul(Q, R), 2)],
                     labels = ['$Q$', '$R$', '$QQ^T$', '$Q^TQ$', '$QR$'],
                     nrows=2, ncols=3, figsize=(14, 10))

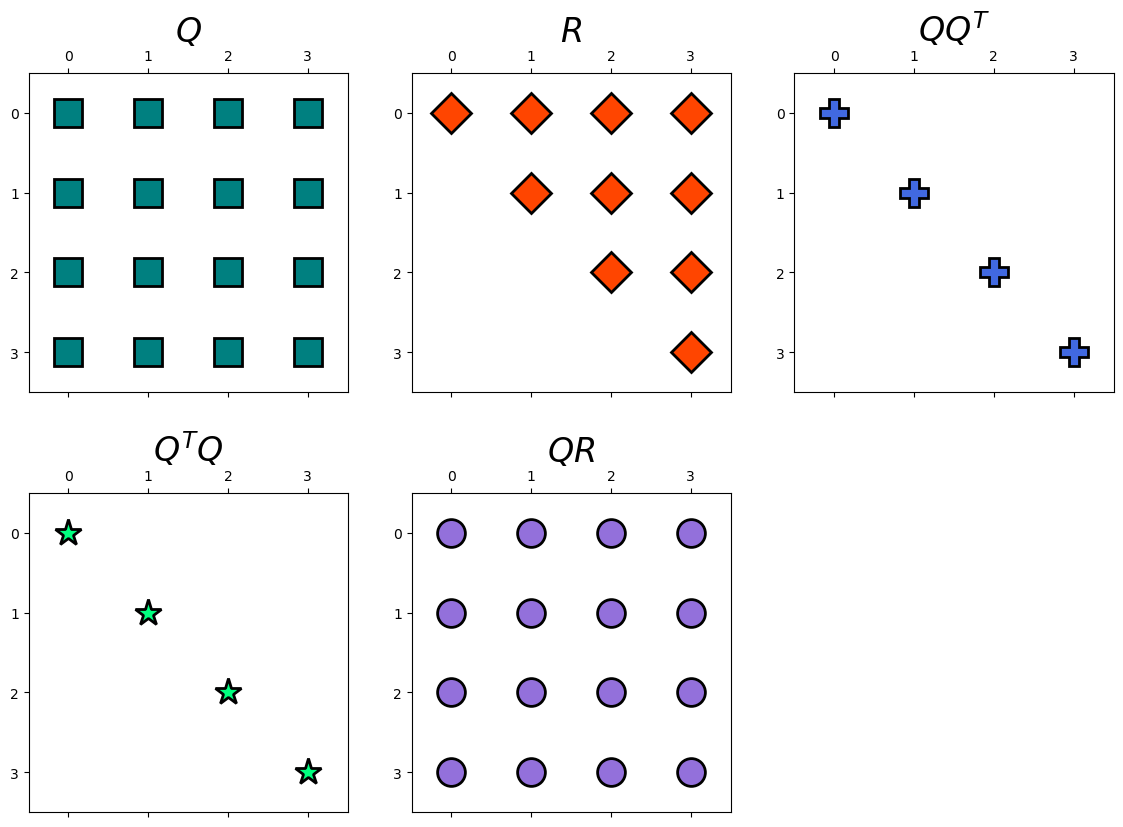
Note that we could get a similar results using function, np.linalg.qr.

import scipy.linalg as linalg
Q, R = linalg.qr(A)
display(Latex(r'Q ='), Matrix(np.round(Q, 2)))
display(Latex(r'R ='), Matrix(np.round(R, 2)))
display(Latex(r'QR ='), Matrix(np.round(Q@R, 2)))
display(Latex(r'QQ^T ='), Matrix(np.round(Q@(Q.T), 2)))
display(Latex(r'Q^TQ ='), Matrix(np.round((Q.T)@Q, 2)))

\[Q =\]

\[\begin{split}\displaystyle \left[\begin{matrix}-0.88 & 0.12 & -0.11 & -0.44\\-0.38 & -0.75 & 0.06 & 0.53\\0.13 & -0.19 & -0.97 & -0.06\\-0.25 & 0.62 & -0.2 & 0.72\end{matrix}\right]\end{split}\]

\[R =\]

\[\begin{split}\displaystyle \left[\begin{matrix}-7.94 & -4.54 & 1.26 & -1.89\\0 & -8.33 & -2.25 & 7.15\\0 & 0 & -3.52 & -0.69\\0 & 0 & 0 & 1.35\end{matrix}\right]\end{split}\]

\[QR =\]

\[\begin{split}\displaystyle \left[\begin{matrix}7.0 & 3.0 & -1.0 & 2.0\\3.0 & 8.0 & 1.0 & -4.0\\-1.0 & 1.0 & 4.0 & -1.0\\2.0 & -4.0 & -1.0 & 6.0\end{matrix}\right]\end{split}\]

\[QQ^T =\]

\[\begin{split}\displaystyle \left[\begin{matrix}1.0 & 0 & 0 & 0\\0 & 1.0 & 0 & 0\\0 & 0 & 1.0 & 0\\0 & 0 & 0 & 1.0\end{matrix}\right]\end{split}\]

\[Q^TQ =\]

\[\begin{split}\displaystyle \left[\begin{matrix}1.0 & 0 & 0 & 0\\0 & 1.0 & 0 & 0\\0 & 0 & 1.0 & 0\\0 & 0 & 0 & 1.0\end{matrix}\right]\end{split}\]

7.5.1. Solving Linear systems using QR factorization

We can solve the linear system \(Ax=b\) for \(x\) using QR factorization. To demonstrate this, we use the following example,

Example: Solve the following linear system using QR decomposition.

\[\begin{align*} \begin{cases} 7\,x_{1}+3\,x_{2}-x_{3}+2\,x_{4}=18\\ 3\,x_{1}+8\,x_{2}+x_{3}-4\,x_{4}=6\\ x_{2}-x_{1}+4\,x_{3}-x_{4}=9\\ 2\,x_{1}-4\,x_{2}-x_{3}+6\,x_{4}=15 \end{cases} \end{align*}\]

Solution:

Let \(A=\left[\begin{array}{cccc} 7 & 3 & -1 & 2\\ 3 & 8 & 1 & -4\\ -1 & 1 & 4 & -1\\ 2 & -4 & -1 & 6 \end{array}\right]\) and \(b=\left[\begin{array}{c} 18\\ 6\\ 9\\ 15 \end{array}\right]\). Then, this linear system can be also expressed as follows,

\[\begin{align*} Ax=(QR)x=Q(Rx)=b. \end{align*}\]

We have,

A = np.array([ [7, 3, -1, 2], [3, 8, 1, -4], [-1, 1, 4, -1], [2, -4, -1, 6] ])
b = np.array([[18],[ 6],[ 9],[15]])
Q, R = myQR(A)
display(Latex(r'Q ='), Matrix(np.round(Q, 2)))
display(Latex(r'R ='), Matrix(np.round(R, 2)))

\[Q =\]

\[\begin{split}\displaystyle \left[\begin{matrix}0.88 & -0.12 & 0.11 & -0.44\\0.38 & 0.75 & -0.06 & 0.53\\-0.13 & 0.19 & 0.97 & -0.06\\0.25 & -0.62 & 0.2 & 0.72\end{matrix}\right]\end{split}\]

\[R =\]

\[\begin{split}\displaystyle \left[\begin{matrix}7.94 & 4.54 & -1.26 & 1.89\\0 & 8.33 & 2.25 & -7.15\\0 & 0 & 3.52 & 0.69\\0 & 0 & 0 & 1.35\end{matrix}\right]\end{split}\]

Now we can solve the following linear systems instead

\[\begin{align*}\begin{cases}Qy = b,\\Rx=y.\end{cases}\end{align*}\]

hd.matrix_decomp_fig(mats = [A, Q, R, np.round(Q@(Q.T), 1), np.round((Q.T)@Q, 1)],
                     labels = ['$A$', '$Q$', '$R$', '$QQ^T$', '$Q^TQ$'],
                     nrows=2, ncols=3, figsize=(14, 10))

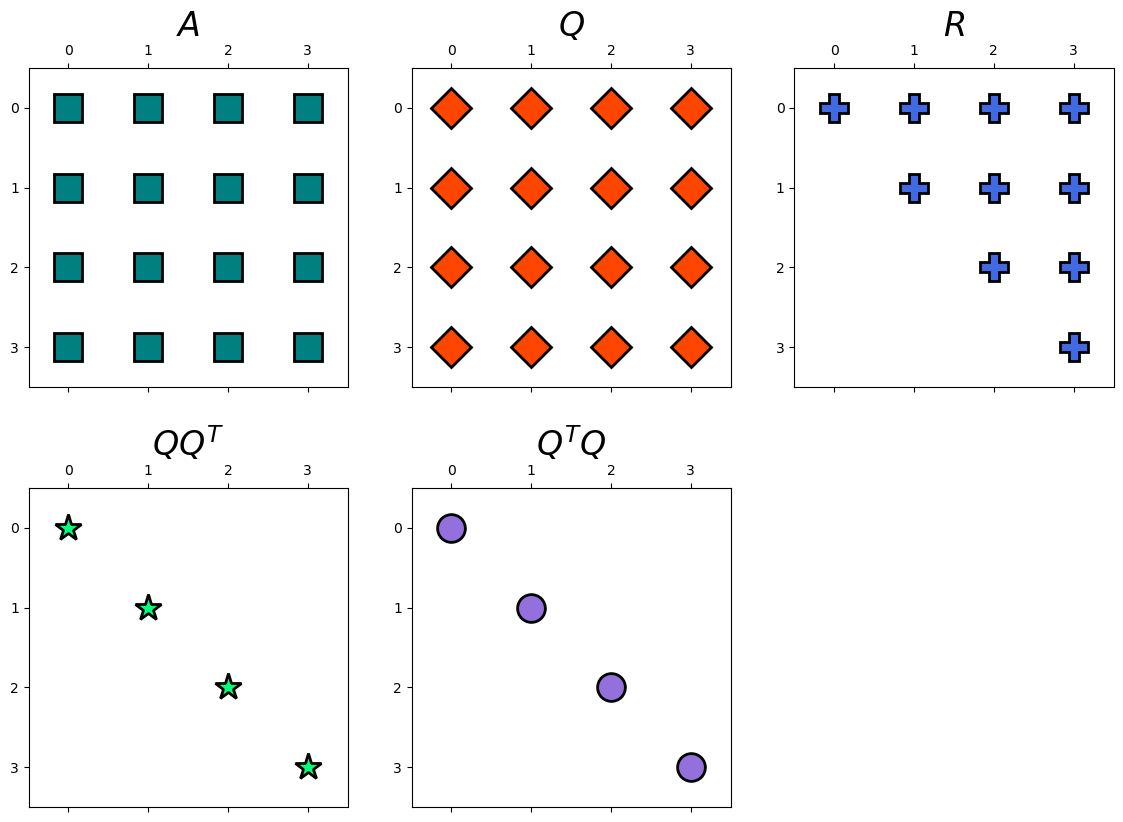
# solving y
y = np.linalg.solve(Q, b)
display(Latex(r'y ='), Matrix(np.round(y, 2)))

\[y =\]

\[\begin{split}\displaystyle \left[\begin{matrix}20.79\\-5.19\\13.32\\5.42\end{matrix}\right]\end{split}\]

# solving Ux=y for x
x = np.linalg.solve(R, y)
display(Latex(r'x ='), Matrix(np.round(x, 2)))

\[x =\]

\[\begin{split}\displaystyle \left[\begin{matrix}1.0\\2.0\\3.0\\4.0\end{matrix}\right]\end{split}\]

Let’s now solve the linear system directly and compare the results.

x_new = linalg.solve(A, b)
display(Latex(r'x ='), Matrix(np.round(x_new, 2)))

\[x =\]

\[\begin{split}\displaystyle \left[\begin{matrix}1.0\\2.0\\3.0\\4.0\end{matrix}\right]\end{split}\]