1.3. Algorithms and Convergence#

1.3.1. Algorithms#

An algorithm is a procedure that applies a finite number of operations on some inputs to produce some outputs. Pseudocodes and flowcharts are often used to describe algorithms.

For example, in pseudocodes, we often use

  • Looping techniques such as For and While loops:

For i = 1, 2, . . . , n
    do something
	
While i < N
    do something
    i = i + 1

  • Condition-controlled statements: If, Else If, Else,…

If Some-Condition
    do something
Else If Some-Other-Condition
    do something else
Else
    something different from the previous two

Example: Write down an algorithm that generates \(\sum_{i = 1}^{N} \sin(x_{i})\) for given values of \(x_{1}\), \(x_{2}\), \(\ldots\), \(x_{n}\).

Solution:

INPUT: N, x1, x2, . . . , xN.
OUTPUT SUM of sin(xi) for i = 1,2,..., N
i=1 xi.
Step 1: Set SUM = 0. ( Initialize accumulator.)
Step 2:
For i = 1, 2, . . . , N do
   set SUM = SUM + sin(xi). ( Add the next term.)
Step 3: OUTPUT (SUM);
STOP.

For generating a flowchart, we need to pay attention to the meaning of each shape. Generally, there is a rounded edge rectangular shape for start/end, rectangular for process, Rhombus shape for decision, and arrows for connecting them. Please see this page for more details.

For the above algorithm, we have,

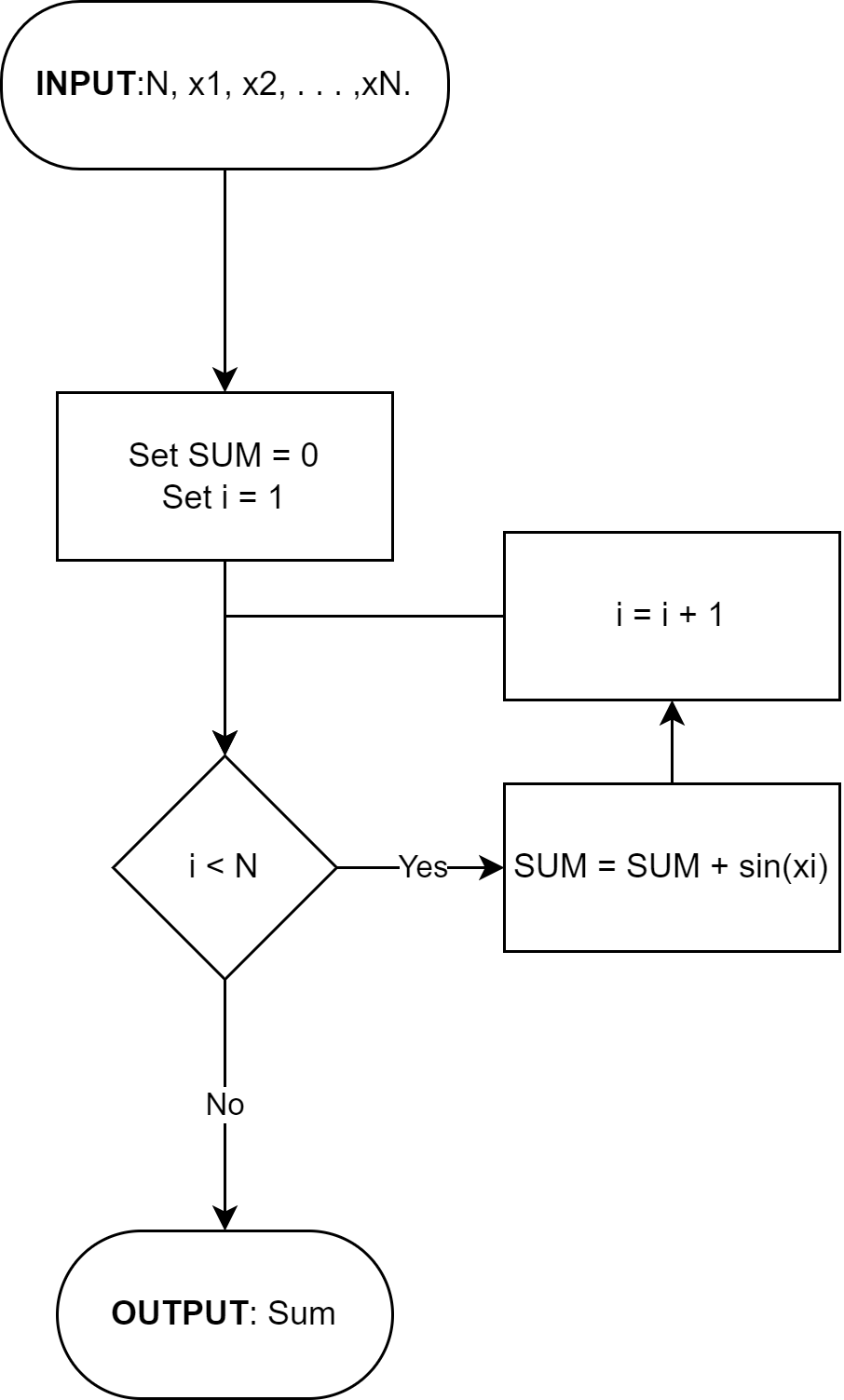
../_images/Flowchart_Example.png

Fig. 1.1 Flowchart Example#