7.1. Gaussian elimination for Linear Systems of Equations

Definition: System of linear equations

A system of equations is a collection of equations. For example, the following \(m\) equations form a system of (linear) equations.

(7.1)\[\begin{align} \begin{cases} a_{11}x_1+\ldots+a_{1n}x_{n}=b_1\\ a_{21}x_1+\ldots+a_{2n}x_{n}=b_2\\ \vdots \\ a_{m1}x_1+\ldots+a_{mn}x_{n}=b_m. \end{cases} \end{align}\]

In terms of summation notation, the above linear equation can be written as

\[\begin{align*} \sum_{j = 1}^{n} a_{ij}\,x_{ij} = b_{i},\quad i = 1, 2, 3, \ldots, m. \end{align*}\]

Definition: Consistent and inconsistent linear systems

A system of equations is called inconsistent when there is no solution for this system of equations, and it is called consistent when there is at least one solution for it.

We start this section with an example. Consider the following system

\[\begin{align*} \begin{cases} 3x_1 +2x_2 - x_3 + x_4 =-1\\ 2x_1 - x_3 +2x_4 = 0\\ 3x_1 + x_2 +2x_3 +5x_4 = 2 \end{cases} \end{align*}\]

This system of linear equations has three equations and four variables. We can express this in the form of a matrix (an array of numbers) as follows

\[\begin{align*} \left[\begin{array}{cccc|c} 3 & 2 & -1 & 1 & -1\\ 2 & 0 & -1 & 2 & 0\\ 3 & 1 & 2 & 5 & 2 \end{array}\right] \end{align*}\]

This matrix is called the augmented matrix of the system.

Definition: Augmented Matrix of a Linear System

For the following system of equations \begin{align} \begin{cases} a_{11}x_1+\ldots+a_{1n}x_{n}=b_1\ a_{21}x_1+\ldots+a_{2n}x_{n}=b_2\ \vdots \ a_{m1}x_1+\ldots+a_{mn}x_{n}=b_m, \end{cases} \end{align*} the augmented matrix can be expressed as follows \begin{align} \left[\begin{array}{cccc|c} a_{11} & a_{12} & \dots & a_{1n} & b_{1} \ a_{21} & a_{22} & \dots & a_{2n} & b_{2} \ \vdots & \vdots & \ddots & \vdots & \vdots \ a_{m1} & a_{m2} & \dots & a_{mn} & b_{m}\ \end{array}\right] \end{align*}

Example: Express the following linear system in the augmented matrix form.

\[\begin{align*} \begin{cases} x_1 + 2x_2 - 2x_3 + x_4 + x_5 =2\\ 2x_1 + x_2 + 3x_3 - x_4 =-1\\ x_2 -4x_3 + 3x_4 + x_5 =1\\ \end{cases} \end{align*}\]

Solution: We have,

\[\begin{align*} \left[\begin{array}{ccccc|c} 1 & 2 & -2 & 1 & 1 & 2\\ 2 & 1 & 3 & -1 & 0 & -1\\ 0 & 1 & -4 & 3 & 1 & 1\\ \end{array}\right] \end{align*}\]

Definition: Elementary Operations

The following operations, called elementary operations, can routinely be performed on systems of linear equations to produce equivalent systems.

• Interchange two equations.

• Multiply one equation by a nonzero number.

• Add a multiple of one equation to a different equation.

In hand calculations (and in computer programs) we manipulate the rows of the augmented matrix rather than the equations.

Definition: Elementary row operations

Elementary row operations on a matrix:

• Interchange two rows.

• Multiply one row by a nonzero number.

• Add a multiple of one row to a different row.

Note that in the previous example,

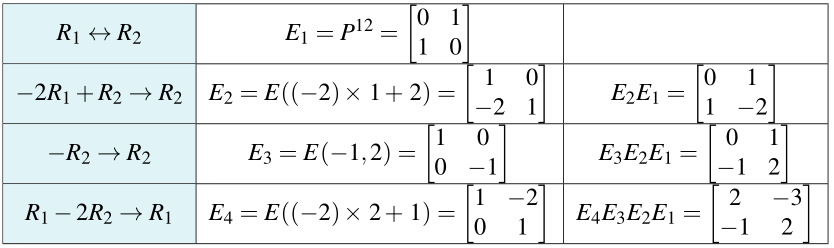
Definition: Equivalent Matrices

The matrix \(B\) is equivalent to the matrix \(A\) if \(B\) can be produced by a sequence of elementary row operations starting with \(A\).

Gaussian Algorithm

For a matrix \(A\),

• Step 1. If the matrix \(A\) only consists entirely of zeros, stop. It is already in REF.

• Step 2. Otherwise, identify the first column from the left comprising a nonzero entry (let’s call this entry \(a\)) and move the row containing that entry to the top position.

• Step 3. Now multiply the new top row by \(1/a\) to produce a leading 1.

• Step 4. By subtracting multiples of that row from rows underneath it, make each entry below the leading 1 zero. This completes the first row, and all additional row operations are conducted on the rest of the rows.

• Step 5. Repeat steps 1 – 4 on the matrix composed of the remaining rows. The process is carried out iteratively until either no rows remain at step 5 or the remaining rows consist entirely of zeros.

Definition: Back-Substitution

Back-substitution is a process of solving a linear system of equations using its REF or RREF. In this process, the last equation is solved first, then the second last equation is solved next, etc.

Example: Solve the following linear system using back-substitution.

\[\begin{align*} \begin{cases} x_{1}+2\,x_{2}+3\,x_{3}=2\\ 4\,x_{1}-3\,x_{2}+x_{3}=-3\\ x_{2}-2\,x_{1}+3\,x_{3}=5 \end{cases} \end{align*}\]

Solution: The corresponding augmented matrix is

\[\begin{align*} \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ 4 & -3 & 1 & -3\\ -2 & 1 & 3 & 5 \end{array}\right]. \end{align*}\]

Use the first row to make the first entry of the second row and third row zero. That is

\[\begin{align*} \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ {4} & -3 & 1 & -3\\ -2 & 1 & 3 & 5 \end{array}\right] &\Rightarrow{-4 R_{1} +R_{2} \rightarrow R_{2}}\Rightarrow \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ 0 & -11 & -11 & -11\\ -2 & 1 & 3 & 5 \end{array}\right] \end{align*}\]

and

\[\begin{align*} \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ 0 & -11 & -11 & -11\\ {-2} & 1 & 3 & 5 \end{array}\right] &\Rightarrow{2 R_{1} +R_{3} \rightarrow R_{3}}\Rightarrow \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ 0 & -11 & -11 & -11\\ 0 & 5 & 9 & 9 \end{array}\right] \end{align*}\]

Multiply the second row by -1/11 to create a leading 1. We have

\[\begin{align*} \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ 0 & {-11} & -11 & -11\\ 0 & 5 & 9 & 9 \end{array}\right] &\Rightarrow{-\frac{1}{11}R_{2} \rightarrow R_{2}}\Rightarrow \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ 0 & 1 & 1 & 1\\ 0 & 5 & 9 & 9 \end{array}\right] \end{align*}\]

By subtracting 5 times of the second row from the third row, make entry below the leading 1 zero.

\[\begin{align*} \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ 0 & 1 & 1 & 1\\ 0 & {5} & 9 & 9 \end{array}\right] &\Rightarrow{-5 R_{2} +R_{3} \rightarrow R_{3}}\Rightarrow \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ 0 & 1 & 1 & 1\\ 0 & 0 & 4 & 4 \end{array}\right] \end{align*}\]

Finally, we can multiply the last row by 1/4 to create a leading 1. That is

\[\begin{align*} \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ 0 & 1 & 1 & 1\\ 0 & 0 & {4} & 4 \end{array}\right] &\Rightarrow{\frac{1}{4}R_{3} \rightarrow R_{3}}\Rightarrow \left[\begin{array}{ccc|c} {1} & 2 & 3 & 2\\ 0 & {1} & 1 & 1\\ 0 & 0 & {1} & 1 \end{array}\right] \end{align*}\]

This REF augmented matrix is equivalent to the following linear system:

\[\begin{align*} \begin{cases} x_{1}+2\,x_{2}+3\,x_{3}=2,\\ x_{2}+x_{3}=1,\\ x_{3}=1. \end{cases} \end{align*}\]

Therefore, \(x_{1}=-1\), \(x_{2}=0\) and \(x_{3}=1\).

Theorem: Gaussian elimination

For a square matrix \(A\), there exists at least one non-singular matrix \(M\) such that

(7.2)\[\begin{align} U = E\,A. \end{align}\]

where \(U\) is an upper triangular matrix.

First, assume that \(A\) is a given \(n\times n\) square matrix as follows with none of the entries on its main diagonal is zero. Then, let \(\tilde{A}^{(1)}\) be the augmented matrix defined as follows,

\[\begin{align*} \tilde{A}^{(1)} = \left[\begin{array}{cccc|c} a_{11} & a_{12} & \dots & a_{1n} & a_{1,n+1} \\ a_{21} & a_{22} & \dots & a_{2n} & a_{2,n+1} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn} & a_{n,n+1}\\ \end{array}\right]. \end{align*}\]

Observe that the above matrix is a \(n \times (n+1)\) matrix. \newpage Assume that \(a_{ij}^{(k)}\), for \(2\leq k \leq n\), denotes the \(ij\)-th entry of matrix \(\tilde{A}^{(k)}\) which is defined using entries of matrix \(\tilde{A}^{(k-1)}\) as follows,

\[\begin{align*} a_{ij}^{(k)} = \begin{cases} a_{ij}^{(k-1)}, & \mbox{when } 1 \leq i \leq k-1 \mbox{ and } 1\leq j \leq n+1,\\ 0, & \mbox{when } i \geq k \mbox{ and } 1\leq j \leq k-1,\\ a_{ij}^{(k-1)} -\dfrac{a_{i,k-1}^{(k-1)}}{a_{k-1,k-1}^{(k-1)}}a_{k-1,j}^{(k-1)}, & \mbox{when } k \leq i \leq n \mbox{ and } k\leq j \leq n+1, \end{cases} \end{align*}\]

and

\[\begin{align*} \tilde{A}^{(k)} = \left[\begin{array}{cccccccc|c} a_{11}^{(1)} & a_{12}^{(1)} & \dots & & a_{1,k-1}^{(1)} & a_{1,k}^{(1)} & \dots & a_{1n}^{(1)} & a_{1,n+1}^{(1)} \\ 0 & a_{22}^{(2)} & \dots & & a_{2,k-1}^{(2)} & a_{2,k}^{(2)} & \dots & a_{2n}^{(2)} & a_{2,n+1}^{(2)} \\ \vdots & & & & \vdots & \vdots & & \vdots & \vdots \\ \vdots & & & & a_{k-1,k-1}^{(k-1)} & a_{k-1,k}^{(k-1)} & \dots & a_{k-1,n}^{(k-1)} & a_{k-1,n+1}^{(k-1)} \\ \vdots & & & & 0 & a_{k,k}^{(k)} & \dots & a_{k,n}^{(k)} & a_{k,n+1}^{(k)} \\ \vdots & & & & 0 & \vdots & & \vdots & \vdots \\ 0 & \dots & \dots & \dots & 0 & a_{n,k}^{(k)} & \dots & a_{n,n}^{(k)} & a_{n,n+1}^{(k)} \\ \end{array}\right]. \end{align*}\]

Here, \(\tilde{A}^{(k)}\) denotes the equivalent linear system for which the variable \(x_{k-1}\) has just been removed from equations \(E_{k}\), \(E_{k+1}\), \ldots , \(E_{n}\).

Observe that if any of \(a_{11}^{(1)}\), \(a_{22}^{(2)}\), \ldots, \(a_{n-a}^{(n-1,n-1)}\) is zero, the above process fails. For this reason, we use \textbf{pivot element}.

Example: Represent the linear system

\[\begin{align*} &E_1:~x_1 + 2x_2 - 2x_3 + x_4 + x_5 =2\\ &E_2:~2x_1 + x_2 + 3x_3 - x_4 =-1\\ &E_3:~x_2 -4x_3 + 3x_4 + x_5 =1\\ \end{align*}\]

as an augmented matrix and use Gaussian Elimination to find its solution.

Solution: The corresponding augmented matrix is

\[\begin{align*} \tilde{A}^{(1)} = \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ 4 & -3 & 1 & -3\\ -2 & 1 & 3 & 5 \end{array}\right]. \end{align*}\]

Performing the following operations,

\[\begin{align*} & E_{2} -4 E_{1} \rightarrow E_{2},\\ & E_{3} + 2 E_{1}\rightarrow E_{3}. \end{align*}\]

Thus,

\[\begin{align*} \tilde{A}^{(2)} = \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ 0 & -11 & -11 & -11\\ 0 & 5 & 9 & 9 \end{array}\right] \end{align*}\]

Also, we have perform the following operation \(E_{3} -\dfrac{5}{11}E_{2} \rightarrow E_{3}\),

\[\begin{align*} \tilde{A}^{(3)} \left[\begin{array}{ccc|c} 1 & 2 & 3 & 2\\ 0 & -11 & -11 & -11\\ 0 & 0 & 4 & 4 \end{array}\right] \end{align*}\]

Now, we have,

\[\begin{align*} x_{3} & = \frac{4}{4} = 1,\\ x_{2} & = \frac{-11 + 11\,x_{3}}{-11} = \frac{-11 + 11}{-11} = 0,\\ x_{1} & = \frac{2 - 2\,x_{2} - 3\,x_{3}}{1} = \frac{2 - 2(0) - 3(1)}{1} = -1. \end{align*}\]