1.12. Recursion

Recursion extends programming into the realm of self-replication. This technique permits a function to call itself, breaking complex problems into simpler sub-problems. Consequently, programmers can craft elegant solutions for challenges that might be unwieldy to address directly.

Recursion is a powerful programming concept in which a function calls itself to solve a problem. It is a fundamental technique used in many algorithms and data structures. Recursive functions break down a complex problem into smaller subproblems, solve each subproblem, and combine their results to obtain the final solution. A recursive function typically consists of two main components:

1. Base case: A condition that determines when the function should stop calling itself and return a result directly. It prevents the function from calling itself indefinitely and causing infinite recursion.

2. Recursive case: The part of the function where it calls itself with modified arguments to solve a smaller version of the original problem.

Here’s a simple example of a recursive function to calculate the factorial of a number:

def factorial(n):
    if n == 0:
        return 1  # Base case: 0! is 1
    else:
        return n * factorial(n - 1)  # Recursive case: n! = n * (n-1)!

Let’s break it down step by step:

1. The factorial function takes one argument, n, which represents the number for which we want to calculate the factorial.

2. Inside the function, there’s an if statement that checks if n is equal to 0. This is known as the base case of the recursion. In mathematics, 0 factorial (0!) is defined to be 1. So, if n is 0, the function immediately returns 1, and the recursion stops. This is essential because it provides a base condition to end the recursive calls.

3. If n is not 0, the else block is executed. Here’s what happens in the else block:

   a. n * factorial(n - 1): This is the recursive case. It calculates n times the factorial of (n - 1). This is based on the fact that the factorial of n is defined as n! = n * (n - 1)!.

   b. The factorial(n - 1) part is a recursive call to the factorial function with n - 1 as its argument. This means that the function will be called again with a smaller value of n. This process continues until n reaches 0 (the base case), at which point the recursion stops.

   c. The intermediate results are accumulated as each recursive call returns. For example, if you call factorial(4), it calculates 4 * factorial(3), then 3 * factorial(2), then 2 * factorial(1), and finally 1 * factorial(0). When factorial(0) is reached, it returns 1, and the results are propagated back up the recursion stack to calculate the final result.

4. The function returns the result of the recursive calculation, which is the factorial of the original n provided as an argument.

Here’s a sample breakdown of how factorial(4) would be calculated step by step:

factorial(4) = 4 * factorial(3)
             = 4 * (3 * factorial(2))
             = 4 * (3 * (2 * factorial(1)))
             = 4 * (3 * (2 * (1 * factorial(0))))
             = 4 * (3 * (2 * (1 * 1)))
             = 4 * (3 * (2 * 1))
             = 4 * (3 * 2)
             = 4 * 6
             = 24

So, factorial(4) returns 24, which is the factorial of 4. This recursive function is a classic example of how recursion can be used to solve problems where the solution depends on smaller instances of the same problem.

Example: Let’s call the factorial function with an example:

result = factorial(5)
print(result)  # Output: 120 (5! = 5 * 4 * 3 * 2 * 1 = 120)

120

Note

Recursion is a powerful technique, but it can also lead to performance issues and stack overflow errors if not used correctly or if the base case is not properly defined. It’s essential to ensure that the recursion stops at some point and that the problem size reduces with each recursive call.

1.12.1. Stack diagrams for recursive functions

Stack diagrams are a visual representation of the call stack, which is a data structure used to manage function calls in a program. When a function is called, a new frame (also known as an activation record) is created on the call stack to store the function’s local variables and execution context. When the function returns, its frame is removed from the stack.

For recursive functions, the call stack grows as the function calls itself multiple times. Each recursive call creates a new frame on top of the previous one. When the base case is reached, the function calls start returning, and the frames are removed from the stack one by one.

Let’s consider the same example of the factorial function from the previous explanation and visualize its stack diagram:

def factorial(n):
    if n == 0:
        return 1  # Base case: 0! is 1
    else:
        return n * factorial(n - 1)  # Recursive case: n! = n * (n-1)!

result = factorial(5)
print(result)

120

The stack diagram for the factorial(5) function call will look like this:

|-- factorial(5)
|   |-- factorial(4)
|   |   |-- factorial(3)
|   |   |   |-- factorial(2)
|   |   |   |   |-- factorial(1)
|   |   |   |   |   |-- factorial(0)
|   |   |   |   |   |-- return 1
|   |   |   |   |-- return 1 * 1 = 1
|   |   |   |-- return 2 * 1 = 2
|   |   |-- return 3 * 2 = 6
|   |-- return 4 * 6 = 24
|-- return 5 * 24 = 120

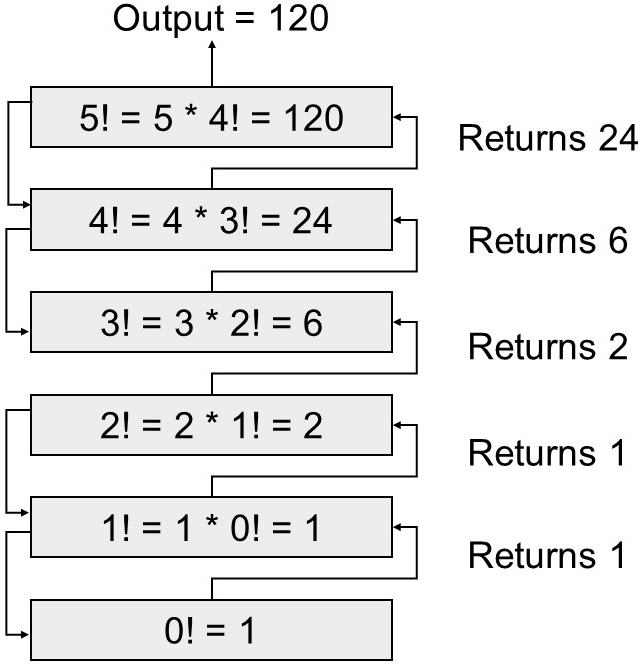
Fig. 1.14 Visual representation 5!.

Each entry in the stack diagram represents a frame for a specific recursive call. The function factorial(5) calls factorial(4), which in turn calls factorial(3), and so on until the base case factorial(0) is reached. Then, the function returns its result to the previous frame, and the process continues until the final result of factorial(5) is calculated.

Stack diagrams provide a clear visual representation of the function calls and the flow of execution in recursive functions. They are a helpful tool for understanding how recursion works and how the call stack manages function calls in a program.

1.12.2. Infinite recursion

Infinite recursion occurs when a recursive function calls itself indefinitely without reaching a base case to stop the recursion. As a result, the call stack continues to grow with each recursive call, eventually leading to a “RecursionError” or “maximum recursion depth exceeded” error in Python.

Here’s an example of a recursive function with no base case, leading to infinite recursion:

def infinite_recursion():
    print("This function is calling itself indefinitely!")
    infinite_recursion()

infinite_recursion()

If you run the code above, you will see that the function keeps printing the message “This function is calling itself indefinitely!” repeatedly until a “RecursionError” occurs.

To prevent infinite recursion, it is crucial to define a base case in the recursive function. The base case serves as a termination condition that stops the recursion and allows the function to start returning values instead of making more recursive calls. Without a base case, the function will keep calling itself without an end.

Let’s modify the previous example to include a base case:

def not_a_infinite_recursion(counter):
    print(f"This function is calling itself {counter} times.")
    if counter > 1:
        not_a_infinite_recursion(counter - 1)

not_a_infinite_recursion(5)

This function is calling itself 5 times.
This function is calling itself 4 times.
This function is calling itself 3 times.
This function is calling itself 2 times.
This function is calling itself 1 times.

It’s essential to be careful while using recursion and ensure that the base case is properly defined to avoid infinite recursion and potential stack overflow errors. Recursive functions should reduce the problem size with each recursive call, eventually leading to the termination condition (base case).

1.12.3. Keyboard input

In Python, you can take keyboard input from the user using the built-in input() function. The input() function reads a line of text entered by the user and returns it as a string. You can then store this input in a variable or use it directly in your program.

Here’s a simple example of how to use the input() function to take keyboard input from the user:

# Taking user input and storing it in a variable
name = input("Enter your name: ")
print("Hello, " + name + "!")

# Taking user input and using it directly
age = int(input("Enter your age: "))  # We use int() to convert the input to an integer
print("You will be " + str(age + 1) + " years old next year.")

In the first example, the program prompts the user to enter their name, and the input is stored in the variable name. The program then prints a greeting message using the user’s name.

In the second example, the program prompts the user to enter their age, and the input is read as a string by default. We use the int() function to convert the input to an integer so that we can perform arithmetic operations on it. The program then prints a message about the user’s age next year.

Keep in mind that input() always returns a string. If you need to perform calculations or comparisons on the input as numbers, you should explicitly convert it to the appropriate data type (e.g., int, float) using int() or float().

Note

When using input(), the program will wait for the user to enter text and press the “Enter” key before moving on to the next line of code.