12.9. Deep Learning Architectures#
Deep learning architectures are the models or frameworks of artificial neural networks that consist of multiple layers of interconnected units or neurons that can learn from data and perform various tasks, such as image processing, speech recognition, natural language processing, and more. Deep learning architectures can be classified into different categories based on their structure, function, and learning method. Some of the most common and popular categories of deep learning architectures are:
Autoencoder (AE): These are neural networks that use unsupervised learning to learn a compressed representation of the input data, such as images or text. AE networks consist of an encoder and a decoder, where the encoder reduces the dimensionality of the input data, and the decoder reconstructs the original data from the compressed representation. AE networks can reconstruct the original data from the compressed representation, and are widely used for data compression, denoising, and feature extraction tasks [Liang et al., 2021, Prakash et al., 2021].
Convolutional neural networks (CNNs): These are neural networks that use convolutional layers to extract features from the input data, such as images or text. Convolutional layers apply filters or kernels to the input data, and produce feature maps that capture the local patterns or structures of the data. CNNs are especially good at recognizing patterns and objects in images, and are widely used for computer vision tasks [Khan et al., 2022, Mou and Jin, 2018].
Deep Belief Network (DBN): These are neural networks that use unsupervised learning to learn a hierarchical representation of the input data, such as images or text. DBN networks consist of multiple layers of RBMs, where the output of one RBM is the input of the next RBM. DBN networks can learn complex and abstract features of the data, and are widely used for data generation, recognition, and classification tasks [Hua et al., 2015, Lopes and Ribeiro, 2014].
Deep Stacking Network (DSN): These are neural networks that use supervised learning to learn a hierarchical representation of the input data, such as images or text. DSN networks consist of multiple layers of FNNs, where the output of one FNN is the input of the next FNN. DSN networks can learn complex and nonlinear functions of the data, and are widely used for regression and classification tasks [Deng et al., 2013, Fred et al., 2016, Lopes and Ribeiro, 2014].
Feedforward neural networks (FNNs): These are the simplest and most basic type of neural networks that have a linear or sequential structure. They consist of an input layer, an output layer, and one or more hidden layers in between. The information flows from the input layer to the output layer in a forward direction, without any feedback loops or cycles. FNNs can learn to approximate any function, and are widely used for regression and classification tasks [Bishop, 1995, Fine, 2006, Ketkar and Moolayil, 2021].
Generative adversarial network (GAN): These are neural networks that use unsupervised learning to generate realistic and diverse data samples, such as images or text. GAN networks consist of two competing networks: a generator and a discriminator, where the generator tries to fool the discriminator by producing fake data, and the discriminator tries to distinguish between real and fake data. GAN networks can create novel and high-quality data samples, and are widely used for image synthesis, style transfer, and text generation tasks [Kaddoura, 2023, Yadav et al., 2023].
Gated Recurrent Unit (GRU): These are another special type of RNNs that have reset and update gates that can control the flow of information within the hidden layers. GRU networks are simpler and faster than LSTM networks, and achieve similar or better performance on some tasks. GRU networks are widely used for natural language processing and speech recognition tasks [Dey and Salem, 2017, Salem, 2022].
Graph neural network (GNN): These are neural networks that use graph structures to model the input data, such as social networks or molecules. GNN networks consist of multiple layers of graph convolution or graph attention, where each layer updates the node features based on the neighboring nodes and edges. GNN networks can learn the complex and non-Euclidean relationships of the data, and are widely used for graph analysis, node classification, and link prediction tasks [Hamilton, 2020, Wu et al., 2022].
Long short-term memory (LSTM): These are a special type of RNNs that have memory cells or gates that can store or forget information over long periods of time. LSTM networks can handle long and complex sequences of data, and overcome the problems of vanishing or exploding gradients that affect RNNs. LSTM networks are widely used for machine translation, text generation, and sentiment analysis tasks [Graves, 2012].
Neural Turing machine (NTM): These are neural networks that use external memory to store and manipulate information, such as symbols or sequences. NTM networks consist of a controller and a memory, where the controller reads and writes to the memory using attention mechanisms. NTM networks can learn to perform algorithmic tasks and generalization, and are widely used for program synthesis, reasoning, and meta-learning tasks[Faradonbe and Safi-Esfahani, 2020, Malekmohamadi Faradonbe et al., 2020].
Recurrent neural networks (RNNs): These are neural networks that have feedback loops or connections between the hidden layers, which allow them to process sequential data, such as speech or text. RNNs can learn from the previous inputs and outputs, and capture the temporal or sequential dependencies of the data. RNNs are widely used for natural language processing and speech recognition tasks [Alam et al., 2023, Salem, 2022].
Restricted Boltzmann Machine (RBM): These are neural networks that use unsupervised learning to learn a probabilistic distribution of the input data, such as images or text. RBM networks consist of a visible layer and a hidden layer, where the visible layer represents the input data, and the hidden layer represents the latent variables or features. RBM networks can generate new data samples from the learned distribution, and are widely used for data generation, recommendation, and collaborative filtering tasks [Sabry, 2023, Yan, 2020].
Self-Organizing Map (SOM): These are neural networks that use unsupervised learning to create a low-dimensional representation of the input data, such as images or text. SOM networks can cluster or group similar data points together, and preserve the topological or spatial relationships of the data. SOM networks are widely used for data visualization, dimensionality reduction, and anomaly detection tasks [Kohonen, 2012, Vellido et al., 2019].
Transformer: These are neural networks that use attention mechanisms to process sequential data, such as speech or text. Attention mechanisms allow the network to focus on the relevant parts of the input and output sequences, and encode the dependencies and relationships of the data. Transformer networks can handle long and complex sequences of data, and are widely used for natural language processing and speech recognition tasks [Bhattacharya et al., 2022, Xia et al., 2023, Xiong et al., 2023].
These are some of the categories of deep learning architectures that are used for various applications.
12.9.1. Choice between TensorFlow and PyTorch#
All the mentioned architectures, namely Autoencoder (AE), Convolutional Neural Networks (CNNs), Deep Belief Network (DBN), Deep Stacking Network (DSN), Feedforward Neural Networks (FNNs), Generative Adversarial Network (GAN), Gated Recurrent Unit (GRU), Graph Neural Network (GNN), Long Short-Term Memory (LSTM), Neural Turing Machine (NTM), Recurrent Neural Networks (RNNs), Restricted Boltzmann Machine (RBM), Self-Organizing Map (SOM), and Transformer, are available in both TensorFlow and PyTorch frameworks. These frameworks provide comprehensive support for implementing and training various deep learning architectures, allowing researchers and practitioners to choose the framework that aligns with their preferences and requirements.
TensorFlow and PyTorch are two of the most popular and widely used frameworks for deep learning. They both offer high-level APIs and low-level interfaces for building, training, and deploying various deep learning models. They also support GPU and distributed computing, as well as various tools and libraries for data processing, visualization, debugging, and testing.
The choice of framework depends on several factors, such as the type of problem, the level of customization, the ease of use, the performance, the documentation, and the community support. There is no definitive answer to which framework is better, as they both have their own strengths and weaknesses. Some of the main differences and similarities between TensorFlow and PyTorch are summarized in the table below [Dai et al., 2021, Novac et al., 2022]:
Feature |
TensorFlow |
PyTorch |
|---|---|---|
Programming style |
Static graph |
Dynamic graph |
Debugging |
Difficult |
Easy |
Deployment |
Easy |
Difficult |
Performance |
Fast |
Slow |
Documentation |
Comprehensive |
Sparse |
Community |
Large |
Small |
Ecosystem |
Rich |
Poor |
As for the deep learning architectures, they are designed for different purposes and applications, such as image recognition, natural language processing, generative modeling, reinforcement learning, etc. Each architecture has its own advantages and disadvantages, and the choice of architecture depends on the task, the data, and the desired outcome. Some of the main characteristics and applications of the architectures you mentioned are summarized in the table below [Alzubaidi et al., 2021, Kwak et al., 2023]:
Architecture |
Characteristics |
Applications |
|---|---|---|
Autoencoder (AE) |
A type of neural network that learns to reconstruct its input by encoding it into a latent representation and decoding it back. |
Data compression, denoising, anomaly detection, dimensionality reduction, etc. |
Convolutional Neural Network (CNN) |
A type of neural network that uses convolutional layers to extract features from images or other structured data. |
Image recognition, object detection, face recognition, semantic segmentation, etc. |
Deep Belief Network (DBN) |
A type of neural network that consists of multiple layers of Restricted Boltzmann Machines (RBMs) stacked on top of each other. |
Feature extraction, unsupervised learning, generative modeling, etc. |
Deep Stacking Network (DSN) |
A type of neural network that consists of multiple layers of simple classifiers stacked on top of each other. |
Supervised learning, classification, regression, etc. |
Feedforward Neural Network (FNN) |
A type of neural network that consists of multiple layers of neurons connected in a forward direction. |
Supervised learning, classification, regression, function approximation, etc. |
Generative Adversarial Network (GAN) |
A type of neural network that consists of two competing networks: a generator that tries to produce realistic samples from a latent distribution, and a discriminator that tries to distinguish between real and fake samples. |
Image synthesis, style transfer, image inpainting, super-resolution, etc. |
Gated Recurrent Unit (GRU) |
A type of recurrent neural network that uses gated units to control the flow of information through time. |
Sequence modeling, natural language processing, speech recognition, etc. |
Graph Neural Network (GNN) |
A type of neural network that operates on graph-structured data, such as social networks, molecular graphs, knowledge graphs, etc. |
Graph analysis, node classification, link prediction, graph generation, etc. |
Long Short-Term Memory (LSTM) |
A type of recurrent neural network that uses memory cells to store and access information over long time intervals. |
Sequence modeling, natural language processing, speech recognition, etc. |
Neural Turing Machine (NTM) |
A type of neural network that augments a recurrent neural network with an external memory that can be read and written by the network. |
Memory-augmented learning, algorithm learning, program synthesis, etc. |
Recurrent Neural Network (RNN) |
A type of neural network that has recurrent connections that allow it to process sequential data. |
Sequence modeling, natural language processing, speech recognition, etc. |
Restricted Boltzmann Machine (RBM) |
A type of neural network that consists of two layers of stochastic units: a visible layer that represents the input, and a hidden layer that represents the latent features. |
Unsupervised learning, feature extraction, generative modeling, etc. |
Self-Organizing Map (SOM) |
A type of neural network that consists of a grid of neurons that learn to map high-dimensional input data to low-dimensional output space. |
Data visualization, clustering, dimensionality reduction, etc. |
Transformer |
A type of neural network that uses attention mechanisms to encode and decode sequential data. |
Natural language processing, machine translation, text generation, etc. |
Remark
MLP can play a versatile role in various deep learning architectures, contingent upon the specific task and dataset. For instance:
MLP serves as a fundamental deep learning architecture for supervised learning tasks, encompassing classification and regression, particularly well-suited for structured or tabular data. It excels at approximating intricate functions by adjusting its weights based on input-output pairs. However, MLP may exhibit limitations when confronted with sequential or spatial data, as it lacks the inherent capacity to capture temporal or spatial dependencies in the data.
MLP functions as a pivotal component within broader deep learning architectures like CNNs, RNNs, or Transformers, where it assumes specialized roles in executing specific functions or subtasks. For instance, it can act as a fully connected layer at the conclusion of a CNN, facilitating classification on extracted features. Alternatively, within a Transformer architecture, MLP can operate as a feed-forward network to process attention outputs. Moreover, MLP finds application as a classifier or regressor atop other architectures such as RNNs or GNNs, contributing to the generation of final outputs.
Note
Within this course, a comprehensive exploration of the aforementioned methods is beyond our scope. Instead, we will offer illustrative examples of common deep learning applications within the realm of engineering.
12.9.2. Convolutional Neural Network (CNN)#
Convolutional Neural Networks (CNNs) constitute a specialized category of neural networks meticulously designed for the efficient processing of grid-like data, notably applied to domains such as image analysis. This architectural paradigm draws inspiration from the intricacies of visual processing observed in the human brain. Central to the functionality of CNNs are the convolutional layers, acting as specialized filters adept at detecting intricate patterns and features within the input data.
I assume you want to refine your text by adding some information about the benefits and drawbacks of rescaling, as well as some examples of other preprocessing layers. Here is a possible way to do that:
12.9.2.1. Rescaling Layer#
The “Rescaling Layer” is a crucial preprocessing step in neural networks, especially when dealing with image-based tasks. Its primary purpose is to rescale input images to specific dimensions, thereby ensuring consistency in pixel values and creating a standardized input format for subsequent layers in the neural network.
In the context of image processing, rescaling involves adjusting the pixel values of input images to a predefined range, commonly between 0 and 1. This normalization serves several important functions. Firstly, it helps prevent numerical instabilities that may arise if pixel values span a broad range, which could impact the stability and convergence of the learning process. Secondly, normalization mitigates the impact of varying illumination conditions or color scales in images, promoting a consistent representation across different inputs.
Consider an example where an image has pixel values ranging from 0 to 255 (common in grayscale images). The Rescaling Layer would transform these values to a standardized range, such as between 0 and 1, by dividing each pixel value by 255. This normalization ensures that the neural network processes images in a consistent manner, regardless of the original intensity scale.
By rescaling pixel values to a standardized range, the neural network becomes less sensitive to variations in absolute intensity across different images. Instead, it focuses on learning the relative relationships between pixel values, enabling the network to extract meaningful patterns and features from the images. This is vital for effective learning, as it ensures that the network’s parameters are adjusted based on the intrinsic structure of the data rather than variations in intensity.
The tf.keras.layers.Rescaling layer in TensorFlow is a convenient tool for rescaling the pixel values of input data. This layer is particularly useful in preprocessing images before feeding them into a neural network. The primary purpose of Rescaling is to normalize the pixel values, ensuring that they fall within a specified range.
The Rescaling layer in TensorFlow is a preprocessing layer that rescales input data to a specified range. It is often employed for normalizing pixel values in images, promoting stability and uniformity in the input data. The layer takes two parameters: scale and offset. The rescaling formula is given by:
Scale: A multiplier to rescale the input data.
Offset: An additive term to adjust the rescaled values.
Example:
import tensorflow as tf
# Assume input_data is an image tensor with pixel values in the range [0, 255]
input_data = tf.constant([[100.0, 150.0, 200.0], [50.0, 75.0, 25.0]])
# Define the Rescaling layer with a scale of 1/255 to normalize pixel values to [0, 1]
rescaling_layer = tf.keras.layers.Rescaling(scale=1./255)
# Apply Rescaling to the input_data
normalized_data = rescaling_layer(input_data)
# Display the original and normalized data
print("Original Data:")
print(input_data)
print("\nNormalized Data:")
print(normalized_data)
Original Data:
tf.Tensor(
[[100. 150. 200.]
[ 50. 75. 25.]], shape=(2, 3), dtype=float32)
Normalized Data:
tf.Tensor(
[[0.3921569 0.5882353 0.7843138 ]
[0.19607845 0.29411766 0.09803922]], shape=(2, 3), dtype=float32)
In this example, the Rescaling layer is employed with a scale of \( \frac{1}{255} \). The layer effectively scales the pixel values in the input_data tensor, transforming them to the normalized range [0, 1]. This normalization is particularly useful in image processing tasks, contributing to the stability and convergence of neural networks during training. The tf.keras.layers.Rescaling layer serves as a straightforward and efficient way to perform rescaling on input data.
However, rescaling is not the only preprocessing step that can be applied to input data. Depending on the task and the data, other preprocessing layers may be more suitable or necessary. Some of the other preprocessing layers that can be used in TensorFlow are:
CenterCrop: A layer that crops the central portion of the input data, reducing the spatial dimensions and removing the irrelevant or noisy parts of the data. This layer can be useful for focusing on the most important features of the data, such as the face in a portrait image.
RandomCrop: A layer that randomly crops a portion of the input data, introducing some variation and diversity in the data. This layer can be useful for augmenting the data and preventing overfitting, as it exposes the network to different perspectives and scenarios of the data.
RandomFlip: A layer that randomly flips the input data horizontally or vertically, creating a mirror image of the data. This layer can also be useful for augmenting the data and preventing overfitting, as it simulates different orientations and viewpoints of the data.
RandomRotation: A layer that randomly rotates the input data by a certain angle, creating a rotated image of the data. This layer can also be useful for augmenting the data and preventing overfitting, as it mimics different rotations and angles of the data.
Normalization: A layer that normalizes the input data by subtracting the mean and dividing by the standard deviation of the data. This layer can be useful for standardizing the data and improving the performance of the network, as it makes the data more Gaussian-like and reduces the variance of the data.
These are some of the preprocessing layers that can be used in TensorFlow to transform and enhance the input data. Depending on the task and the data, different combinations and sequences of preprocessing layers can be applied to achieve the best results. Preprocessing is an essential step in neural networks, as it can affect the quality and efficiency of the learning process.
12.9.2.2. Convolutional Layers#
In the realm of CNNs, the input image undergoes a transformative journey through a sequence of convolutional layers. Each of these layers harnesses a collection of filters, featuring small, learnable weights that convolve across the spatial dimensions of the input. This convolutional operation adeptly extracts local patterns, ranging from elementary features like edges to more intricate textures. The progressive movement through these layers facilitates the capturing of hierarchical features, contributing to the network’s ability to discern and comprehend complex structures inherent in the input data.
A critical element within the convolutional layer’s architecture involves the systematic traversal of a convolutional filter across an input matrix.
Example: Consider a 3x3 convolutional filter denoted by the matrix [[0,1,0], [1,0,1], [0,1,0]]. In this convolutional layer, nine distinct convolutional operations unfold, with each operation meticulously applied to a 5x5 input matrix. Crucially, each operation is directed at a unique 3x3 segment of the input matrix. The culmination of these operations results in the creation of a consolidated 3x3 matrix, encapsulating the collective outcomes of the nine individual convolutional processes [Google Developers, 2023].
Let’s delve into the mathematical steps involved:
Input Matrix (5x5):
\[\begin{equation*} I = \begin{bmatrix} 1 & 2 & 3 & 4 & 5 \\ 6 & 7 & 8 & 9 & 10 \\ 11 & 12 & 13 & 14 & 15 \\ 16 & 17 & 18 & 19 & 20 \\ 21 & 22 & 23 & 24 & 25 \\ \end{bmatrix} \end{equation*}\]Convolutional Filter (3x3):
\[\begin{equation*} F = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \\ \end{bmatrix} \end{equation*}\]Convolution Operation at (1,1):
\[\begin{align*} \text{Result}(1,1) & = (1 \times 0) + (2 \times 1) + (3 \times 0) + (6 \times 1) + (7 \times 0) + (8 \times 1) \\ & + (11 \times 0) + (12 \times 1) + (13 \times 0) = 28 \end{align*}\]Result Matrix (Feature Map): The feature map is composed of the results of each convolution operation:
\[\begin{equation*} \text{Feature Map} = \begin{bmatrix} 28 & \text{Result}(1,2) & \text{Result}(1,3) \\ \text{Result}(2,1) & \text{Result}(2,2) & \text{Result}(2,3) \\ \text{Result}(3,1) & \text{Result}(3,2) & \text{Result}(3,3) \\ \end{bmatrix} \end{equation*}\]Continue this process for each position in the matrix.
These numerical values represent the outcome of the convolutional operations, vividly illustrating how the convolutional filter systematically processes the input matrix to yield a discerning and informative feature map.
The tf.keras.layers.Conv2D layer in TensorFlow is a core building block for convolutional neural networks (CNNs). It performs 2D convolutions on input data, typically used for processing images or spatial data. Convolutional layers are essential for extracting hierarchical features from input data, enabling the network to learn hierarchical representations.
# Import numpy for array operations
import numpy as np
# Define the input matrix as a numpy array
input_matrix = np.array([[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10],
[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25]])
# Define the convolutional filter as a numpy array
conv_filter = np.array([[0, 1, 0],
[1, 0, 1],
[0, 1, 0]])
# Define the output matrix as an empty numpy array
output_matrix = np.zeros((3, 3))
# Loop over the input matrix with a stride of 1
for i in range(3):
for j in range(3):
# Extract a 3x3 segment of the input matrix
segment = input_matrix[i:i+3, j:j+3]
# Perform element-wise multiplication and summation
result = np.sum(segment * conv_filter)
# Store the result in the output matrix
output_matrix[i, j] = result
# Print the output matrix
print(output_matrix)
[[28. 32. 36.]
[48. 52. 56.]
[68. 72. 76.]]
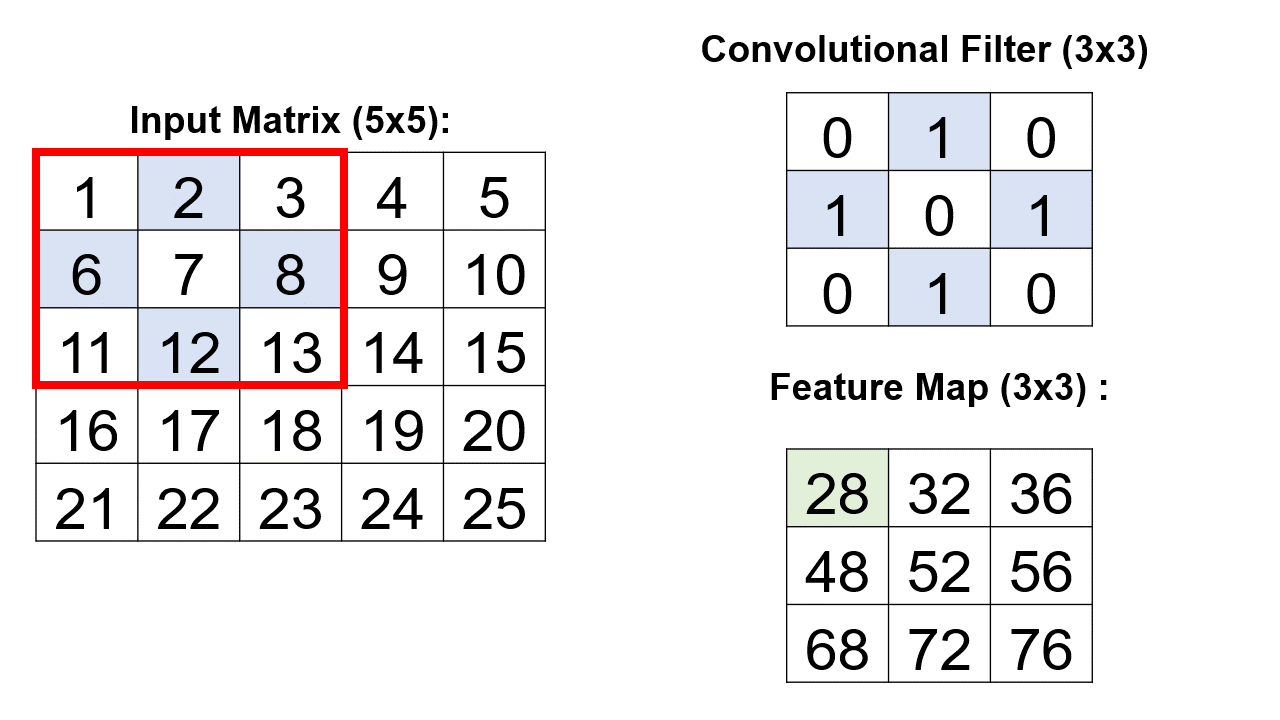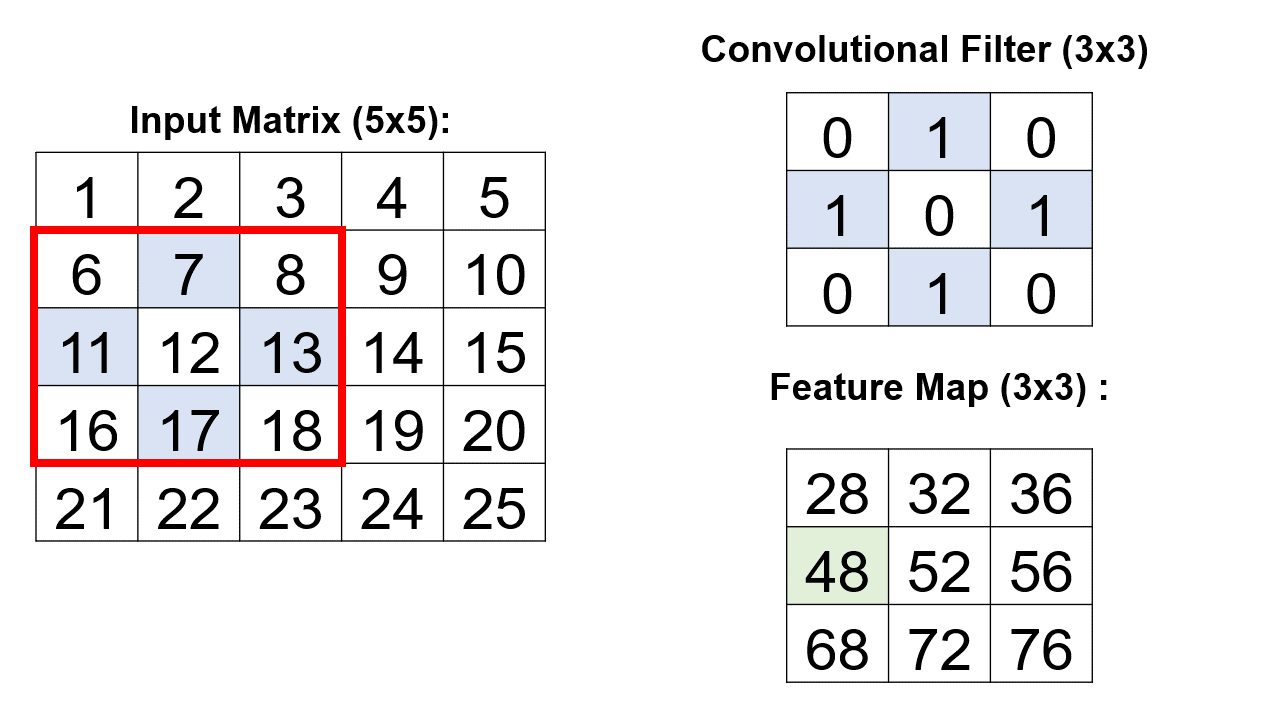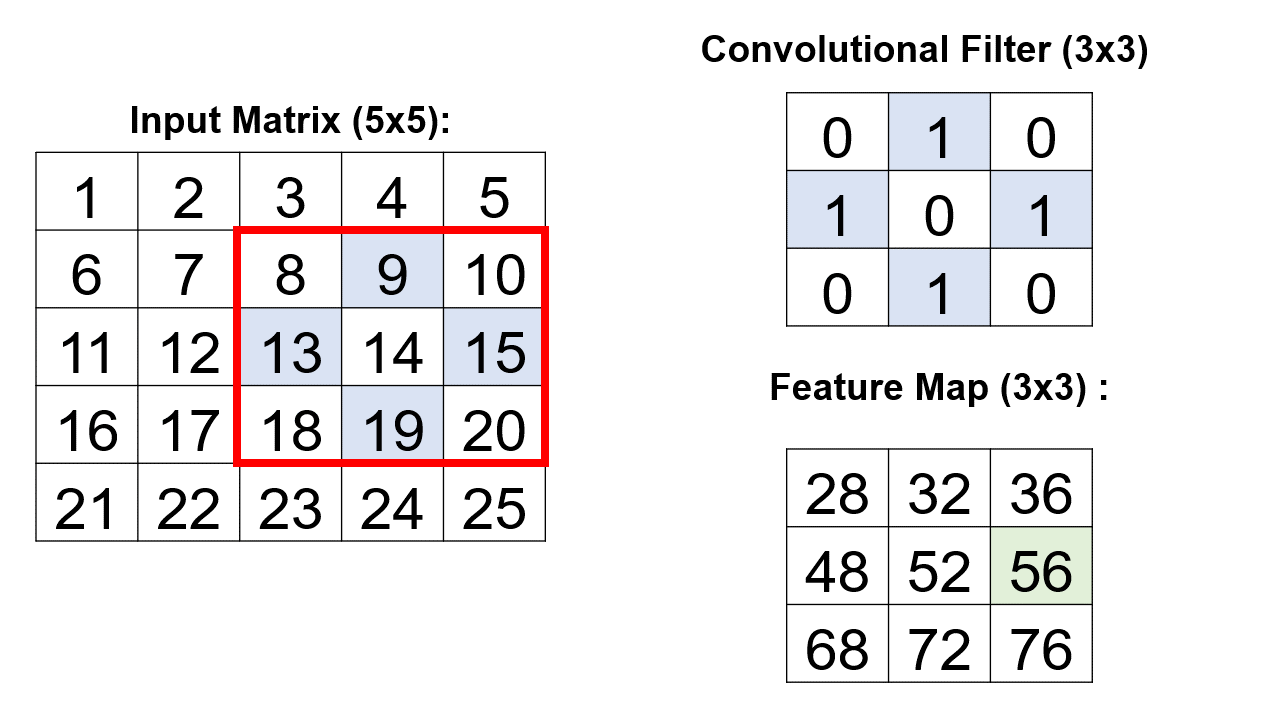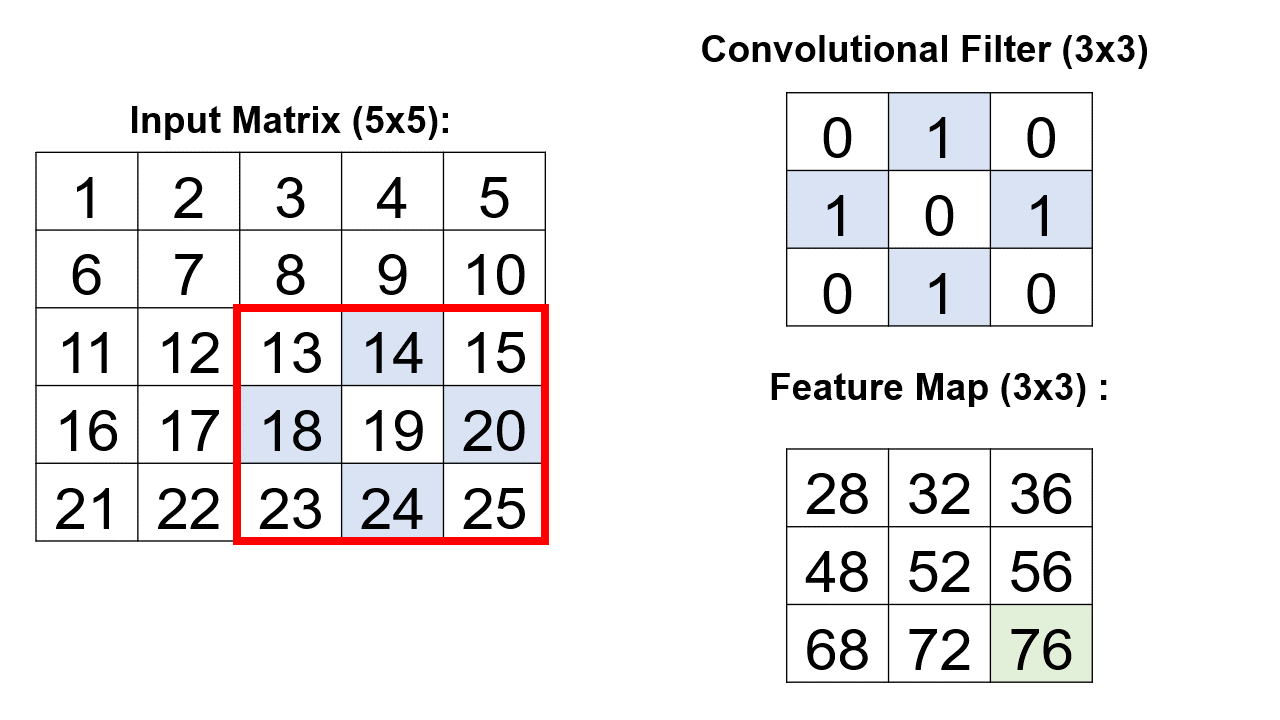
Fig. 12.17 A visual representation of the above example.#
The Conv2D layer in TensorFlow is used for 2D convolutions, applying a set of filters or kernels to input data. These filters slide over the input, performing element-wise multiplication and summing the results to produce feature maps. This process captures local patterns and spatial relationships in the input, making convolutional layers effective for image-related tasks.
The Conv2D layer takes several parameters, such as:
filters: The number of filters or kernels to use in the convolutional layer. This determines the depth or the number of channels of the output feature map. Each filter can learn to detect a different feature from the input data.
kernel_size: The size or shape of the filters or kernels to use in the convolutional layer. This determines the height and width of the region of the input that each filter covers. A common choice is a 3x3 kernel, which can capture local patterns and features effectively.
strides: The number of pixels to move the filters or kernels across the input in each dimension. This determines the spatial resolution or the height and width of the output feature map. A common choice is a stride of 1, which means that the filters move one pixel at a time, preserving the spatial resolution of the input. A larger stride can reduce the spatial resolution and the computational complexity of the layer, but it may also lose some information from the input.
padding: The way to handle the edges of the input in the convolutional layer. This determines whether to add zeros or to ignore the edges of the input when applying the filters or kernels. A common choice is a padding of ‘same’, which means that the input is padded with zeros such that the output feature map has the same spatial resolution as the input. Another choice is a padding of ‘valid’, which means that the input is not padded and the output feature map has a smaller spatial resolution than the input.
activation: The activation function to apply to the output feature map of the convolutional layer. This determines how the output values are transformed into a non-linear range. A common choice is a ReLU activation function, which sets any negative value to zero and preserves any positive value. This can introduce some sparsity and non-linearity in the output feature map, enhancing the learning ability of the layer.
Example:
import tensorflow as tf
# Assume input_data is an image tensor with shape (batch_size, height, width, channels)
input_data = tf.random.normal(shape=(32, 28, 28, 3))
# Define the Conv2D layer with 64 filters, 3x3 kernel size, 1 stride, same padding, and ReLU activation
conv2d_layer = tf.keras.layers.Conv2D(filters=64, kernel_size=3, strides=1, padding='same', activation='relu')
# Apply Conv2D to the input_data
output_data = conv2d_layer(input_data)
# Display the shape of the input and output data
print("Input Data Shape:")
print(input_data.shape)
print("\nOutput Data Shape:")
print(output_data.shape)
Input Data Shape:
(32, 28, 28, 3)
Output Data Shape:
(32, 28, 28, 64)
In this example, the Conv2D layer is applied to the input_data tensor, which has a shape of (32, 28, 28, 3). This means that the input_data consists of 32 images, each with a height of 28 pixels, a width of 28 pixels, and 3 channels (RGB). The Conv2D layer uses 64 filters, each with a size of 3x3, a stride of 1, a padding of ‘same’, and a ReLU activation function. The output_data tensor has a shape of (32, 28, 28, 64). This means that the output_data consists of 32 feature maps, each with a height of 28 pixels, a width of 28 pixels, and 64 channels. Each channel corresponds to a different filter that has learned to detect a different feature from the input_data. The output_data can be fed into the next layer of the network, such as a pooling layer or another convolutional layer.
12.9.2.3. Pooling Layers#
Pooling layers, integral components of convolutional neural network (CNN) architectures, play a crucial role in downsampling spatial dimensions and enhancing computational efficiency while preserving key features. Two prevalent pooling methods, max pooling and average pooling, contribute to this process. In max pooling, the maximum value within a defined region is retained, emphasizing prominent features, while average pooling calculates the average value within a region, providing a smoother representation.
Pooling layers systematically select representative values from specific regions of the input, effectively summarizing the presence of essential features. This strategic downsampling contributes to model efficiency by maintaining crucial information while reducing computational complexity [Google Developers, 2023].
Example: Consider a 2x2 max pooling operation applied to a 4x4 feature map:
The pooling operation selects the maximum value within each 2x2 region, resulting in a downsampled 2x2 pooled map:
This process vividly demonstrates how pooling layers efficiently condense the information in the feature map, retaining essential details for subsequent layers in the neural network [Google Developers, 2023].
# Import numpy for array operations
import numpy as np
# Define the feature map as a numpy array
feature_map = np.array([[2, 4, 1, 7],
[6, 8, 3, 5],
[9, 12, 11, 10],
[14, 13, 15, 16]])
# Define the pooled map as an empty numpy array
pooled_map = np.zeros((2, 2))
# Loop over the feature map with a stride of 2
for i in range(0, 4, 2):
for j in range(0, 4, 2):
# Extract a 2x2 region of the feature map
region = feature_map[i:i+2, j:j+2]
# Select the maximum value within the region
result = np.max(region)
# Store the result in the pooled map
pooled_map[i//2, j//2] = result
# Print the pooled map
print(pooled_map)
[[ 8. 7.]
[14. 16.]]
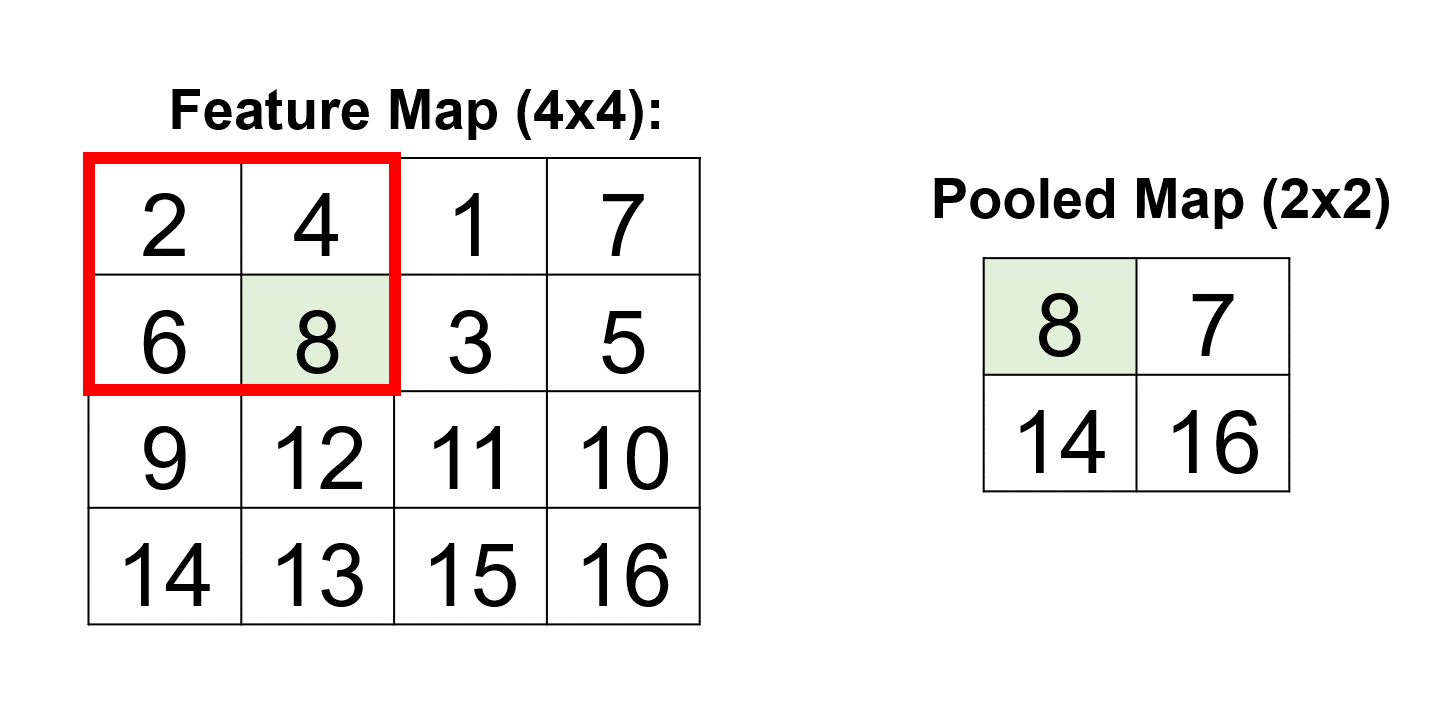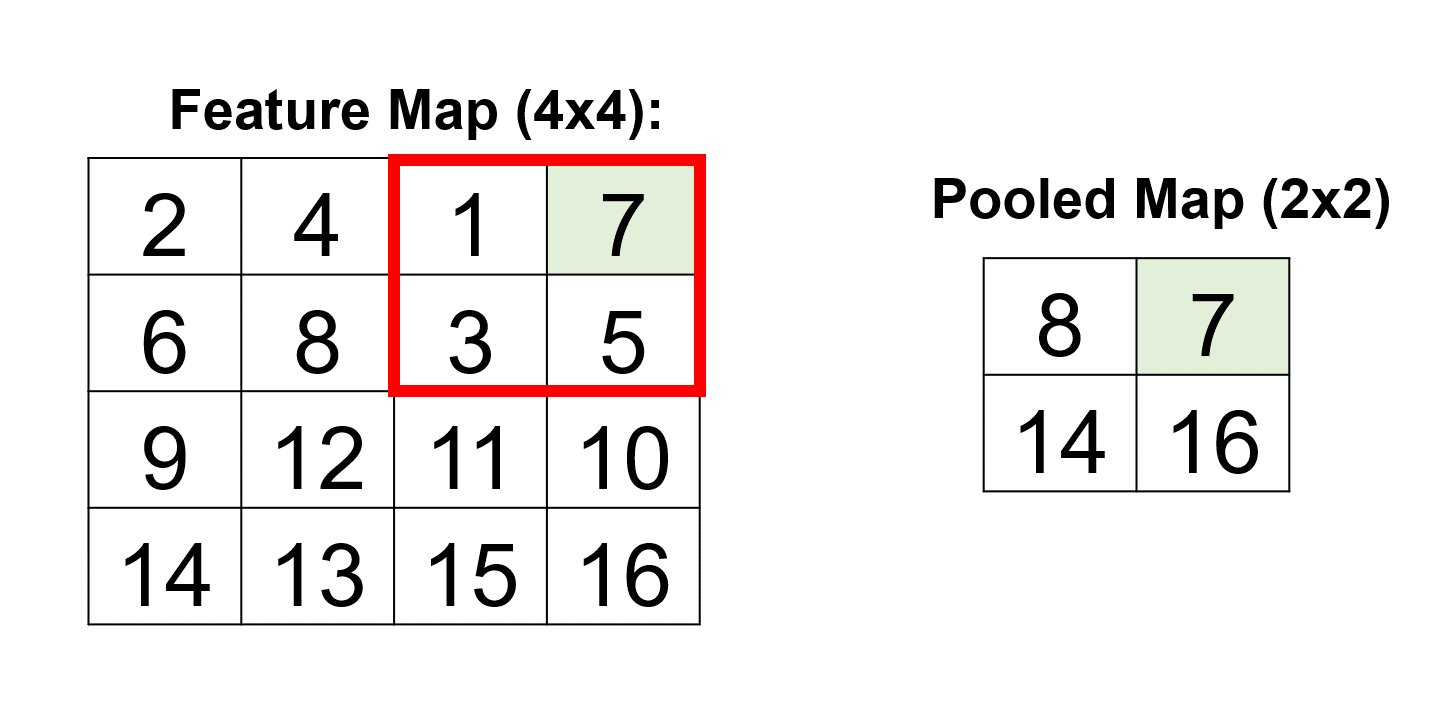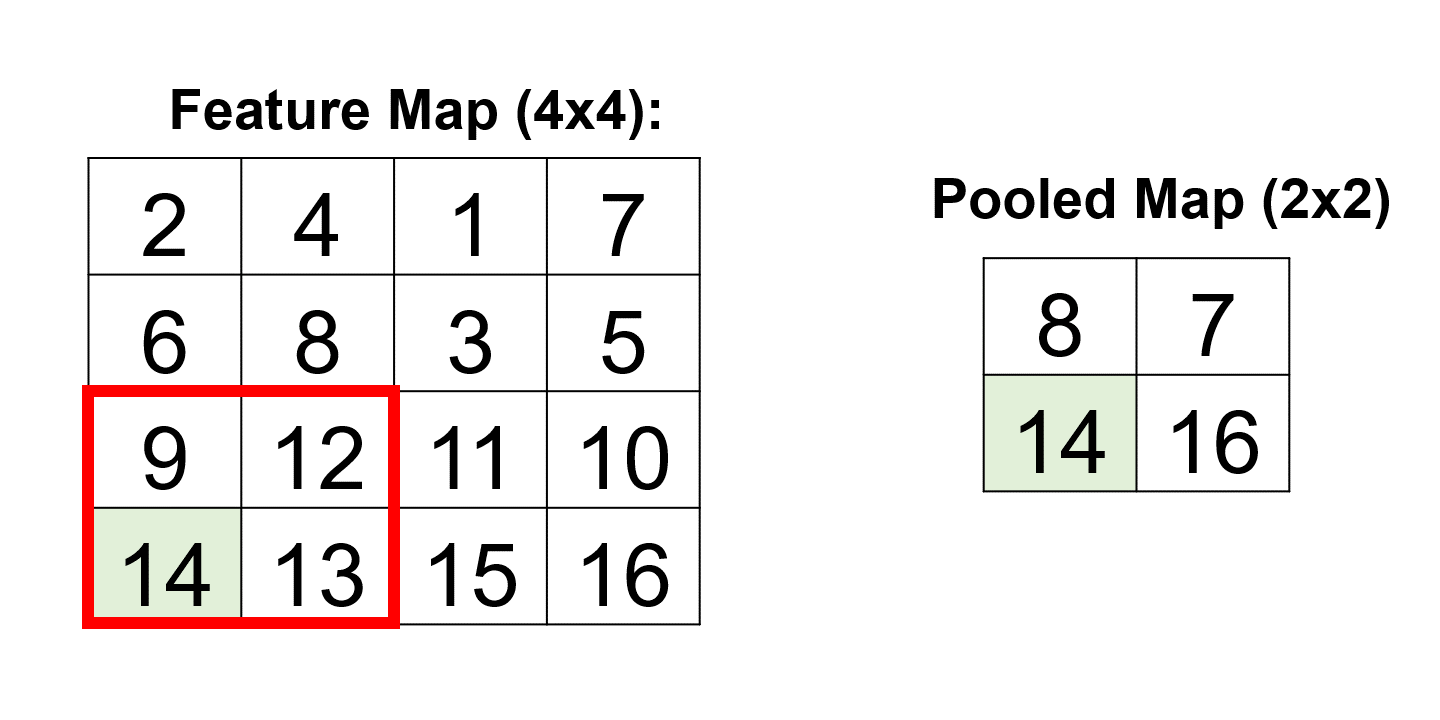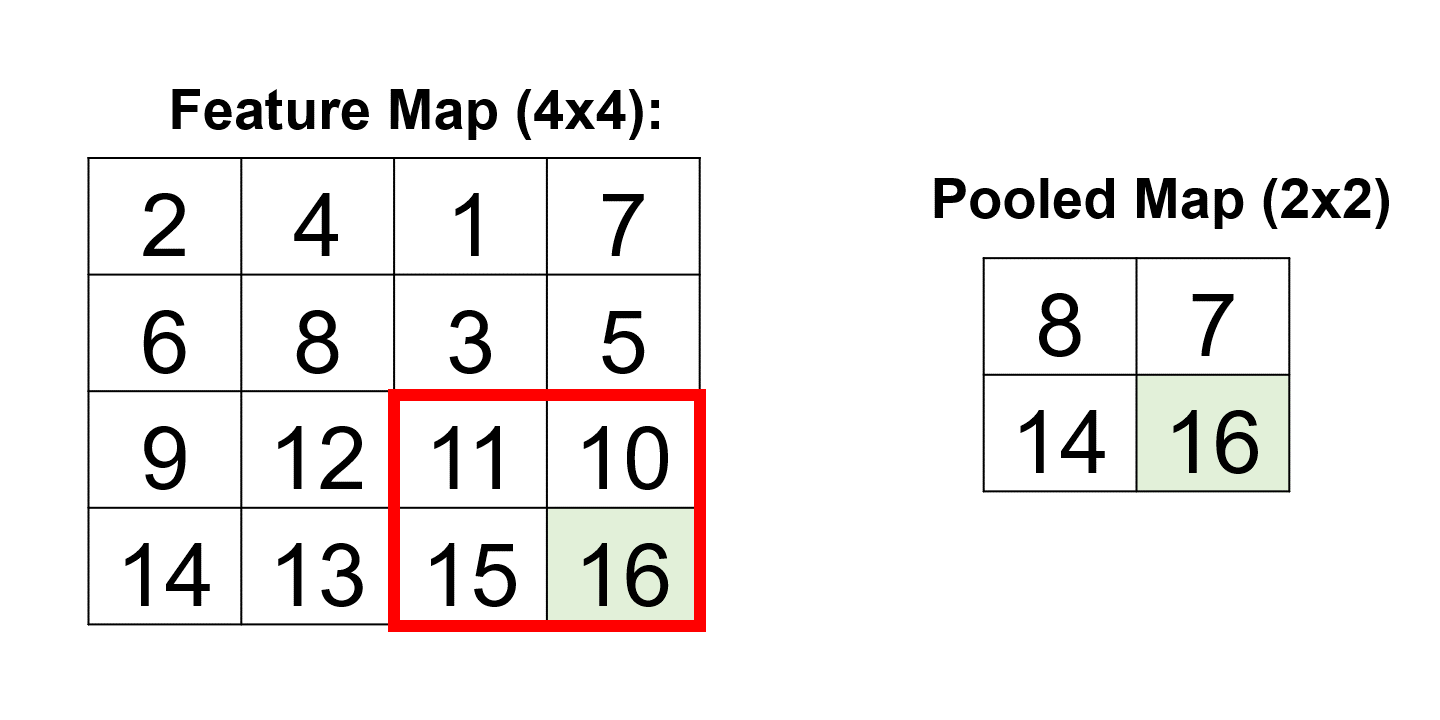
Fig. 12.18 A visual representation of the above example.#
The tf.keras.layers.MaxPooling2D layer in TensorFlow is a pooling layer commonly used in convolutional neural networks (CNNs) for downsampling spatial dimensions. Pooling layers help reduce the spatial resolution of the input data, leading to a more compact representation while retaining essential features. Max pooling is a specific pooling operation where the maximum value within each pooling window is retained.
The MaxPooling2D layer performs 2D max pooling, where it downsamples the spatial dimensions of the input data by selecting the maximum value within each pooling window. This operation is applied independently to different channels of the input data.
he MaxPooling2D layer takes several parameters, such as:
pool_size: The size of the pooling window, typically specified as a tuple (height, width).
strides: The step size for sliding the pooling window over the input.
padding: “valid” (no padding) or “same” (zero-padding to maintain spatial dimensions).
Example:
import tensorflow as tf
# Define a MaxPooling2D layer with a 2x2 pooling window and 'valid' padding
maxpool_layer = tf.keras.layers.MaxPooling2D(pool_size=(2, 2), padding='valid')
# Assuming input_data is a 4D tensor representing an image (batch_size, height, width, channels)
input_data = tf.constant([[[[1.0], [2.0], [3.0], [4.0]],
[[5.0], [6.0], [7.0], [8.0]],
[[9.0], [10.0], [11.0], [12.0]],
[[13.0], [14.0], [15.0], [16.0]]]], dtype=tf.float32)
# Apply MaxPooling2D to the input data
output_data = maxpool_layer(input_data)
# Display the original and pooled data shapes
print("Original Data Shape:", input_data.shape)
print("Pooled Data Shape:", output_data.shape)
Original Data Shape: (1, 4, 4, 1)
Pooled Data Shape: (1, 2, 2, 1)
In this example, a MaxPooling2D layer is defined with a 2x2 pooling window and ‘valid’ padding. The layer is then applied to an example input data tensor, resulting in a downsampled output. Adjust the parameters based on the requirements of your specific CNN architecture. The pool_size determines the size of the pooling window, and padding influences whether zero-padding is applied to maintain spatial dimensions.
However, max pooling is not the only pooling operation that can be applied to input data. Depending on the task and the data, other pooling layers may be more suitable or necessary. Some of the other pooling layers that can be used in TensorFlow are:
AveragePooling2D: A layer that performs 2D average pooling, where it downsamples the spatial dimensions of the input data by selecting the average value within each pooling window. This operation is applied independently to different channels of the input data. Average pooling can provide a smoother representation of the input data, but it may also lose some important features that max pooling can preserve.
GlobalMaxPooling2D: A layer that performs global max pooling, where it downsamples the spatial dimensions of the input data by selecting the maximum value within the entire input. This operation is applied independently to different channels of the input data. Global max pooling can reduce the spatial resolution of the input data to a single value per channel, which can be useful for classification or regression tasks.
GlobalAveragePooling2D: A layer that performs global average pooling, where it downsamples the spatial dimensions of the input data by selecting the average value within the entire input. This operation is applied independently to different channels of the input data. Global average pooling can also reduce the spatial resolution of the input data to a single value per channel, which can be useful for classification or regression tasks.
These are some of the pooling layers that can be used in TensorFlow to downsample and summarize the input data. Depending on the task and the data, different combinations and sequences of pooling layers can be applied to achieve the best results. Pooling is an essential step in convolutional neural networks, as it can affect the quality and efficiency of the learning process.
12.9.2.4. Dropout Layers#
The “Dropout Layer” is a regularization technique used in neural networks, and it specifically refers to the Dropout layer in the context of deep learning models. This layer plays a crucial role in preventing overfitting, a common issue where a model learns to perform exceptionally well on the training data but struggles to generalize to unseen data.
Overfitting occurs when a model becomes too complex and starts memorizing patterns specific to the training data, including noise or outliers, rather than learning the underlying patterns that generalize well to new data. Dropout is a regularization method designed to address this problem.
In a Dropout Layer, during training, a random fraction of neurons (nodes) in the layer is “dropped out” or deactivated. This means that their outputs are set to zero, effectively removing their contribution to the forward pass and backward pass during that specific iteration of training. The fraction of neurons to drop out is a hyperparameter and is typically set between 0.2 and 0.5.
The key idea behind dropout is that it introduces noise and variability during training. By randomly removing neurons, the model becomes less reliant on specific neurons for making predictions, forcing it to learn more robust and generalizable features. This process is akin to training multiple different subnetworks on different subsets of the data, and it helps prevent the model from memorizing noise in the training set.
During inference or prediction, when the model is not being trained, all neurons are active, but their outputs are scaled by the dropout rate. This scaling ensures that the expected output during inference remains similar to what the model learned during training.
The Dropout Layer is a regularization technique that helps prevent overfitting by randomly deactivating a fraction of neurons during training. This introduces robustness and improves the generalization ability of the model, making it more effective on unseen data.
The tf.keras.layers.Dropout layer in TensorFlow is a regularization technique commonly used in neural networks, including convolutional neural networks (CNNs). Dropout helps prevent overfitting by randomly setting a fraction of input units to zero during training. This introduces a form of noise to the network, which encourages the network to be more robust and prevents reliance on specific neurons.
The Dropout layer in TensorFlow is a regularization layer that randomly sets a fraction of input units to zero at each update during training time. This random “dropping out” of units helps prevent overfitting by reducing the reliance on specific neurons. It introduces a level of uncertainty during training, making the network more resilient and improving its generalization to unseen data.
Key Parameter:
rate: The fraction of input units to drop during training. It is a float value between 0 and 1, representing the dropout rate.
Example:
import tensorflow as tf
# Define a Dropout layer with a dropout rate of 0.2
dropout_layer = tf.keras.layers.Dropout(rate=0.2)
# Assuming input_data is a tensor representing the output from a previous layer
input_data = tf.constant([[1.0, 2.0, 3.0, 4.0, 5.0]], dtype=tf.float32)
# Apply Dropout to the input data during training
training_output = dropout_layer(input_data, training=True)
# Display the original and dropout-applied data
print("Original Data:", input_data)
print("Training Output (with Dropout):", training_output)
Original Data: tf.Tensor([[1. 2. 3. 4. 5.]], shape=(1, 5), dtype=float32)
Training Output (with Dropout): tf.Tensor([[0. 2.5 0. 0. 6.25]], shape=(1, 5), dtype=float32)
In this example, a Dropout layer is defined with a dropout rate of 0.2. The layer is then applied to an example input data tensor during training (indicated by the training argument). The output data shows that some of the input units have been randomly set to zero, while the remaining units have been scaled by a factor of 1.25 (the inverse of the dropout rate). This scaling ensures that the expected output during inference remains similar to what the model learned during training.
However, dropout is not the only regularization technique that can be applied to neural networks. Depending on the task and the data, other regularization techniques may be more suitable or necessary. Some of the other regularization techniques that can be used in TensorFlow are:
L1 and L2 regularization: These are techniques that add a penalty term to the loss function based on the magnitude of the weights of the network. L1 regularization adds a penalty proportional to the absolute value of the weights, while L2 regularization adds a penalty proportional to the square of the weights. These penalties discourage the network from having large weights, which can lead to overfitting and instability. L1 and L2 regularization can be applied to any layer that has weights, such as
DenseorConv2D, by using thekernel_regularizerargument and specifying the type and amount of regularization.Batch normalization: This is a technique that normalizes the input or output of a layer by subtracting the mean and dividing by the standard deviation of the batch. Batch normalization helps reduce the internal covariate shift, which is the change in the distribution of the inputs or outputs of a layer due to the updates of the previous layers. Batch normalization can improve the stability and performance of the network, as it makes the network less sensitive to the initialization and learning rate of the weights. Batch normalization can be applied to any layer by adding a
BatchNormalizationlayer before or after the layer.Early stopping: This is a technique that stops the training process when the validation loss stops improving or starts increasing. Early stopping helps prevent overfitting by avoiding training the network for too long, which can cause the network to memorize the training data and lose its generalization ability. Early stopping can be implemented in TensorFlow by using a
EarlyStoppingcallback, which monitors the validation loss and stops the training when a certain condition is met.
12.9.2.5. Flatten Layers#
The “Flatten Layer” is a fundamental component in neural networks, particularly in the context of convolutional neural networks (CNNs). This layer serves the purpose of transforming the multi-dimensional output from preceding convolutional or pooling layers into a one-dimensional (flat) vector. The primary objective is to prepare the data for the transition from convolutional operations to fully connected layers.
In convolutional and pooling layers, the data is processed in a grid-like fashion, extracting hierarchical features from different spatial regions. However, fully connected layers require a one-dimensional input where each neuron is connected to every neuron in the preceding and succeeding layers. The Flatten Layer acts as a bridge between these two types of layers, reshaping the data into a format suitable for fully connected operations.
The operation of the Flatten Layer is conceptually straightforward. It takes the multi-dimensional array output from the preceding layers and rearranges it into a linear sequence. For example, in the case of a 2D input with dimensions (height, width), the Flatten Layer would transform it into a 1D array by concatenating the rows or columns.
This flattening process is essential because fully connected layers are typically used for learning complex relationships and making predictions based on the extracted features. The Flatten Layer ensures that the information captured by convolutional and pooling layers can be effectively utilized by fully connected layers for tasks such as image classification.
The tf.keras.layers.Flatten() layer in TensorFlow is a simple layer that is commonly used in neural networks, especially when transitioning from convolutional layers to fully connected layers. It serves the purpose of flattening the input tensor, converting it from a multi-dimensional tensor into a one-dimensional tensor. This operation is necessary when moving from spatial hierarchies (e.g., image grids) to a linear representation, which is a prerequisite for fully connected layers.
The Flatten() layer in TensorFlow is applied to flatten the input tensor, converting it from a multi-dimensional tensor into a one-dimensional tensor. This is particularly useful when transitioning from convolutional layers, which operate on spatial hierarchies like images, to fully connected layers that require a linear input.
Example:
import tensorflow as tf
# Assume conv_output is a tensor representing the output from a convolutional layer
conv_output = tf.constant([[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]],
[[7.0, 8.0, 9.0], [10.0, 11.0, 12.0]]], dtype=tf.float32)
# Define a Flatten layer
flatten_layer = tf.keras.layers.Flatten()
# Apply Flatten to the convolutional output
flattened_output = flatten_layer(conv_output)
# Display the original and flattened data shapes
print("Original Data Shape:", conv_output.shape)
print("Flattened Data Shape:", flattened_output.shape)
Original Data Shape: (2, 2, 3)
Flattened Data Shape: (2, 6)
In this example, a Flatten() layer is applied to a hypothetical convolutional output tensor. The conv_output tensor has a shape representing a 3D grid. The Flatten() layer converts this tensor into a one-dimensional tensor, which is crucial for passing the data to subsequent fully connected layers.
However, flattening is not the only reshaping operation that can be applied to input data. Depending on the task and the data, other reshaping layers may be more suitable or necessary. Some of the other reshaping layers that can be used in TensorFlow are:
Reshape: A layer that reshapes the input tensor into a specified shape, preserving the number of elements. This layer can be useful for changing the dimensionality or the order of the input data, such as converting a 2D matrix into a 3D tensor or vice versa.
Transpose: A layer that transposes the input tensor, swapping the order of the axes. This layer can be useful for changing the orientation or the alignment of the input data, such as flipping the rows and columns of a matrix or the height and width of an image.
Permute: A layer that permutes the input tensor, rearranging the order of the axes according to a specified pattern. This layer can be useful for changing the format or the layout of the input data, such as converting between different data formats like channels first or channels last.
These are some of the reshaping layers that can be used in TensorFlow to transform and manipulate the input data. Depending on the task and the data, different combinations and sequences of reshaping layers can be applied to achieve the best results. Reshaping is an essential step in neural networks, as it can affect the structure and the representation of the data.
12.9.2.6. Dense Layers (Fully Connected Layers)#
Dense layers, also known as fully connected layers, form a fundamental component in the architecture of neural networks, particularly in feedforward neural networks. In a dense layer, each neuron is connected to every neuron in the preceding and succeeding layers, creating a dense network of interconnected nodes. These layers play a crucial role in learning complex representations and capturing intricate relationships within the input data.
The mathematical operation in a dense layer involves the weighted sum of the input features, followed by the application of an activation function. The weights associated with these connections are learnable parameters, adapted during the training process through optimization algorithms such as gradient descent. This adaptability allows dense layers to learn and extract hierarchical features, enabling the network to understand intricate patterns and make informed predictions.
Example: Consider a simple example of a dense layer with three input features (neurons) and two output neurons. The weights associated with each connection are represented by the matrix \( W \), and the biases for the two neurons are denoted by the vector \( b \). The output \( O \) is computed as follows:
Where:
\( X \) is the input vector \([x_1, x_2, x_3]\),
\( W \) is the weight matrix \begin{equation} W = \begin{bmatrix} w_{11} & w_{12} \ w_{21} & w_{22} \ w_{31} & w_{32} \ \end{bmatrix} \end{equation},
\( b \) is the bias vector \([b_1, b_2]\),
The dot product \( \cdot \) denotes matrix multiplication.
The activation function introduces non-linearity to the model, allowing it to learn and represent complex relationships in the data. Some common choices of activation functions are sigmoid, tanh, relu, softmax, etc. The choice of activation function depends on the type and range of output desired, as well as the characteristics of the input data. For example, sigmoid is often used for binary classification, softmax is used for multi-class classification, relu is used for hidden layers, etc. Different activation functions can have different effects on the output of the layer, such as scaling, shifting, clipping, etc.
The following diagram illustrates the concept of a dense layer and how it connects to the previous and next layers:
I’ll try to create that.
The tf.keras.layers.Dense layer in TensorFlow is a fundamental building block in neural networks, particularly in fully connected or densely connected layers. It represents a layer where each neuron or unit is connected to every neuron in the previous layer. The Dense layer performs a weighted sum of its input, applies an activation function, and produces an output.
Key Parameters:
units: The number of neurons in the layer.
activation: The activation function applied to the layer’s output.
use_bias: Boolean, indicating whether the layer uses a bias term.
kernel_initializer: The initializer for the weights.
bias_initializer: The initializer for the bias terms.
Example:
import tensorflow as tf
# Assume flattened_input is a tensor representing the flattened output from a previous layer
flattened_input = tf.constant([[1.0, 2.0, 3.0]])
# Define a Dense layer with 4 units and 'relu' activation
dense_layer = tf.keras.layers.Dense(units=4, activation='relu')
# Apply Dense to the flattened input
dense_output = dense_layer(flattened_input)
# Display the original and dense layer output
print("Flattened Input Shape:", flattened_input.shape)
print("Dense Output Shape:", dense_output.shape)
print("Dense Output:", dense_output.numpy())
Flattened Input Shape: (1, 3)
Dense Output Shape: (1, 4)
Dense Output: [[0. 0. 0.86555624 0.05669618]]
In this example, a Dense layer is defined with 4 units and ‘relu’ activation. The layer is then applied to a hypothetical flattened input tensor. The weights and biases are automatically initialized, and the activation function (‘relu’ in this case) is applied to the output. The output shape is (1, 4), indicating that there are 4 neurons in the layer. The output values are all zero, because the relu activation function clips any negative values to zero.
Note that the weight matrix for this example is a 3x4 matrix that contains the weights associated with each connection between the input and the output neurons. The weight matrix is randomly initialized when the layer is created, and it is updated during the training process to minimize the loss function. The weight matrix is one of the learnable parameters of the layer, along with the bias vector. You can access the weight matrix of the layer by using the get_weights() method, which returns a list of two elements: the weight matrix and the bias vector. For example, you can print the weight matrix as follows:
# Get the weights of the layer
weights = dense_layer.get_weights()
# The first element of the list is the weight matrix
weight_matrix = weights[0]
# Print the weight matrix
print("Weight Matrix:", weight_matrix)
Weight Matrix: [[-0.20255494 -0.06871521 0.20407951 0.5212424 ]
[ 0.0613094 -0.86144495 -0.44219363 0.8067714 ]
[-0.5033858 -0.86037374 0.515288 -0.69269633]]
The weight matrix, denoted as (W), exhibits a dimensionality of (3, 4), signifying the presence of 3 input features and 4 output neurons within the layer. Each element within (W) encapsulates the weight of the connection linking an input feature to an output neuron. The computational process of the dense_output unfolds as follows:
import numpy as np
# Define the input vector as a numpy array
input_vector = np.array([1.0, 2.0, 3.0])
# Define the weight matrix as a numpy array
# (Same as the aforementioned matrix)
# Define the bias vector as a numpy array
bias_vector = np.array([0.0, 0.0, 0.0, 0.0])
The initial step involves computing the dot product between the input vector and the weight matrix, executed as follows:
# Compute the dot product of the input vector and the weight matrix
dot_product = np.dot(input_vector, weight_matrix)
# Print the dot product
print("Dot Product:", dot_product)
Dot Product: [-1.59009349 -4.37272632 0.86555624 0.05669618]
Subsequently, the second step necessitates the addition of the bias term to each element of the vector. This is accomplished through the element-wise addition operation:
# Add the bias term to each element of the vector
biased_sum = dot_product + bias_vector
# Print the biased sum
print("Biased Sum:", biased_sum)
Biased Sum: [-1.59009349 -4.37272632 0.86555624 0.05669618]
Lastly, the third and final step involves the application of the activation function to each element of the vector. In this instance, the activation function is the rectified linear unit (ReLU), defined as the maximum of zero and the input value. The np.maximum() function facilitates this element-wise maximum operation:
# Apply the activation function to each element of the vector
activation = np.maximum(0, biased_sum) # relu
# Print the activation
print("Activation:", activation)
Activation: [0. 0. 0.86555624 0.05669618]
The output of the layer is the final vector obtained after applying the activation function. The output shape is (4,), indicating that there are 4 neurons in the layer.
