3.5. Python Sets#
3.5.1. Creating Sets#
In Python, you can create a set using the set() constructor or by using curly braces {}. Sets are useful when you want to work with a collection of items where duplicates are not allowed and you don’t care about the order of elements. The key point here is that sets only store unique elements, so any duplicate elements in your input will be automatically removed when creating a set [Python Software Foundation, 2023].
# Creating a set using the set() constructor
my_set = set([1, 2, 3, 4, 5])
# Creating a set using curly braces
another_set = {3, 4, 5, 6}
3.5.2. len(s) - Number of Elements in Set s#
This operation returns the number of elements (cardinality) in the set s.
Example:
# Creating a set 'my_set' with elements {1, 2, 3, 4, 5}
my_set = {1, 2, 3, 4, 5}
# Calculating the length of the set and storing it in 'length'
length = len(my_set) # The length of 'my_set' is 5
# Printing the calculated length
print(length)
5
3.5.3. Membership Testing#
One common use of sets is to perform membership testing. You can easily check if a specific element exists in a set using the in keyword. This is a fast operation for sets, as it’s based on hash tables.
Operation |
Result |
|---|---|
x in s |
Check if element |
x not in s |
Check if element |
# Creating a set 'my_set' with elements {1, 2, 3, 4, 5}
my_set = {1, 2, 3, 4, 5}
# Iterating through a list of elements [1, 3, 10]
for element in [1, 3, 10]:
# Checking if the element is present in the 'my_set' set
if element in my_set:
# Printing a message indicating that the element is in the set
print(f"{element} is in the set.")
else:
# Printing a message indicating that the element is not in the set
print(f"{element} is not in the set.")
1 is in the set.
3 is in the set.
10 is not in the set.
3.5.4. Modifying Sets: Adding, Updating, and Removing Elements#
In Python, sets are dynamic and versatile data structures that allow you to work with collections of unique elements. One of the key features of sets is their ability to be easily modified by adding, updating, or removing elements. This section explores a variety of set operations that enable you to perform these tasks efficiently. We’ll cover essential methods like s.update(t), which adds elements from one set to another, s.add(x) for adding individual elements, and s.remove(x) to remove a specific element. Additionally, we’ll discuss the s.discard(x) method, which removes an element if it’s present without raising an error, and s.pop() which removes an arbitrary element from the set. Furthermore, we’ll examine s.clear() for clearing all elements from a set, and s.copy() to create a shallow copy of a set. Through detailed explanations and illustrative examples, you’ll gain a comprehensive understanding of these operations, equipping you with the tools to modify and manipulate sets to meet your specific programming needs [Python Software Foundation, 2023].
s.update(t)- Return setswith elements added from sett:This operation adds all elements from set
tto the sets. It modifies the original setsby adding elements from sett.Result: The result is set
safter adding all elements from sett.Example:
# Creating 'set1' with elements {1, 2, 3}
set1 = {1, 2, 3}
# Creating 'set2' with elements {3, 4, 5}
set2 = {3, 4, 5}
# Updating 'set1' by merging its elements with 'set2'
set1.update(set2) # After update, set1 is {1, 2, 3, 4, 5}
# Printing the updated 'set1'
print(set1)
{1, 2, 3, 4, 5}
s.add(x)- Add elementxto sets:This operation adds a single element
xto the sets.Result: The result is set
swith the elementxadded.Example:
# Creating 'my_set' with elements {1, 2, 3}
my_set = {1, 2, 3}
# Adding the element 4 to 'my_set'
my_set.add(4) # After adding, my_set is {1, 2, 3, 4}
# Printing the updated 'my_set'
print(my_set)
{1, 2, 3, 4}
s.remove(x)- Remove elementxfrom sets:This operation removes the element
xfrom the sets. Ifxis not present in the set, it raises aKeyError.Result: The result is set
swith the elementxremoved.Example:
# Creating 'my_set' with elements {1, 2, 3, 4}
my_set = {1, 2, 3, 4}
# Removing the element 3 from 'my_set'
my_set.remove(3) # After removal, my_set is {1, 2, 4}
# Printing the updated 'my_set'
print(my_set)
{1, 2, 4}
s.discard(x)- Remove elementxfrom setsif present:This operation removes the element
xfrom the setsif it is present. Ifxis not present, it does nothing, without raising an error.Result: The result is set
swith the elementxremoved if it was present.Example:
# Creating 'my_set' with elements {1, 2, 3, 4}
my_set = {1, 2, 3, 4}
# Removing the element 3 from 'my_set'
my_set.remove(3) # After removal, my_set is {1, 2, 4}
# Printing the updated 'my_set'
print(my_set)
{1, 2, 4}
s.pop()- Remove and return an arbitrary element from sets:This operation removes and returns an arbitrary (randomly selected) element from the set
s. If the set is empty, it raises aKeyError.Result: The result is the element removed from set
s.Example:
# Creating 'my_set' with elements {1, 2, 3, 4}
my_set = {1, 2, 3, 4}
# Popping an arbitrary element from 'my_set'; let's say the popped_element is 3, and my_set is now {1, 2, 4}
popped_element = my_set.pop()
# Printing the popped element
print('Popped Element:', popped_element)
# Printing the updated 'my_set'
print('my_set:', my_set)
Popped Element: 1
my_set: {2, 3, 4}
s.clear()- Remove all elements from sets:This operation removes all elements from the set
s, making it an empty set.Result: The result is an empty set.
Example:
# Creating 'my_set' with elements {1, 2, 3, 4}
my_set = {1, 2, 3, 4}
# Clearing all elements from 'my_set', making it an empty set
my_set.clear() # After clearing, my_set is an empty set
# Printing the updated 'my_set'
print(my_set)
set()
s.copy()- Shallow Copy of Sets:This operation creates a new set that is a shallow copy of the set
s.Result: The result is a new set that is a copy of the original set
s.Example:
# Creating 'original_set' with elements {1, 2, 3}
original_set = {1, 2, 3}
# Creating 'copy_set' as a copy of 'original_set'
copy_set = original_set.copy() # Creates a new set that is a copy of 'original_set'
# Printing the copy_set, which contains the same elements as 'original_set'
print(copy_set)
{1, 2, 3}
Operation |
Result |
|---|---|
|
Modify set |
|
Add element |
|
Remove element |
|
Remove element |
|
Remove and return an arbitrary element from set |
|
Remove all elements from set |
|
Create a new set that is a shallow copy of set |
3.5.5. Subset and Superset Operations#
In the realm of set theory, understanding the relationships between sets is fundamental. Python provides us with convenient methods to examine these relationships, specifically focusing on whether one set is a subset or superset of another. Subsets and supersets are essential concepts when you need to check if all elements in one set are present in another or if a set contains all the elements of another set.
In mathematics, subsets and supersets are fundamental concepts in set theory. Let’s define these concepts:
Subset: A set \(A\) is considered a subset of another set \(B\) if every element of set \(A\) is also an element of set \(B\). In other words, \(A\) is a subset of \(B\) if for every \(x\) in \(A\), \(x\) is also in \(B\). This is denoted as \(A \subseteq B\). If \(A\) is a subset of \(B\) and there is at least one element in \(B\) that is not in \(A\), then \(A\) is called a proper subset of \(B\), denoted as \(A \subset B\).
Superset: A set \(B\) is considered a superset of another set \(A\) if every element of set \(A\) is also an element of set \(B\). In other words, \(B\) is a superset of \(A\) if for every \(x\) in \(A\), \(x\) is also in \(B\). This is denoted as \(B \supseteq A\). If \(B\) is a superset of \(A\) and there is at least one element in \(B\) that is not in \(A\), then \(B\) is called a proper superset of \(A\), denoted as \(B \supset A\).
In mathematical notation:
\(A\) is a subset of \(B\): \(A \subseteq B\)
\(A\) is a proper subset of \(B\): \(A \subset B\)
\(B\) is a superset of \(A\): \(B \supseteq A\)
\(B\) is a proper superset of \(A\): \(B \supset A\)
Example: Let \(A = \{1, 2\}\) and \(B = \{1, 2, 3\}\). In this case, \(A\) is a proper subset of \(B\) (\(A \subset B\)) because all elements of \(A\) (\(1\) and \(2\)) are also elements of \(B\), and there is at least one element in \(B\) that is not in \(A\) (\(3\) is not in \(A\)) .
This section explores the s.issubset(t) and s.issuperset(t) operations, allowing you to perform set comparisons with ease. By grasping these operations, you gain a powerful tool to verify the presence of elements within sets and to determine the containment relationship between sets. Let’s delve into the details of these operations and how they enable you to perform insightful set comparisons in Python [Python Software Foundation, 2023].
Let’s delve into the details of these operations:
A.issubset(B)- Determine if A is a subset of B:This operation tests whether every element in set A is contained within set B. In other words, it verifies if set A is entirely included in set B.
Equivalent:
A <= BResult: The result is
Trueif every element of set A is found in set B; otherwise, the result isFalse.Example:
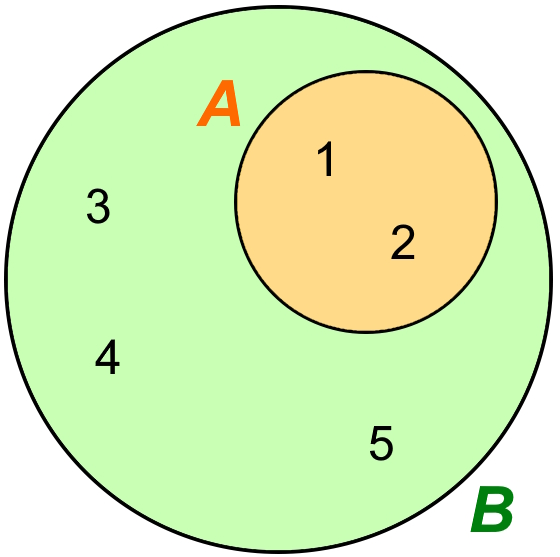
Fig. 3.11 Visual representation of \(A \subseteq B\) and \(B \supseteq A\).#
# Creating set 'A' with elements {1, 2}
A = {1, 2}
# Creating set 'B' with elements {1, 2, 3, 4, 5}
B = {1, 2, 3, 4, 5}
# Checking if 'A' is a subset of 'B' and storing the result; The result is True, because all elements of 'A' are in 'B'
result = A.issubset(B)
# Printing the result
print(result)
True
A.issuperset(B)- Determine if A is a superset of B:This operation examines whether every element in set B is included in set A. In other words, it verifies if set A contains all the elements of set B.
Equivalent:
A >= BResult: The result is
Trueif every element of set B is found in set A; otherwise, the result isFalse.Example:
# Creating set 'A' with elements {1, 2}
A = {1, 2}
# Creating set 'B' with elements {1, 2, 3, 4, 5}
B = {1, 2, 3, 4, 5}
# Checking if 'B' is a superset of 'A' and storing the result; The result is True, because all elements of 'B' are in 'A'
result = B.issuperset(A)
# Printing the result
print(result)
True
These operations are useful when you want to check the relationship between sets, whether one set is entirely contained within another set or if one set contains all the elements of another set. They are often used to perform set comparisons and to ensure that specific elements are present in a given set [Python Software Foundation, 2023].
Operation |
Equivalent |
Result |
|---|---|---|
A.issubset(B) |
A <= B |
Determine if every element in set A is contained within set B. Returns |
A.issuperset(B) |
A >= B |
Examine whether every element in set B is included in set A. Returns |
Remark
In Python, you can check if one set is a proper subset of another using the < operator. Here’s how you can do it:
# Define two sets
A = {1, 2, 3}
B = {1, 2, 3}
# Alternatively, you can use the < operator
is_proper_subset = set_A < set_B
# Print the result
if is_proper_subset:
print("A is a proper subset of B")
else:
print("A is not a proper subset of B")
Output:
A is not a proper subset of B
3.5.6. Set Operations: Combining, Intersecting, and Modifying Sets#
In Python, sets are a versatile tool for handling collections of unique elements, and they come with a powerful set of operations that allow you to manipulate and compare sets effectively. This section delves into fundamental set operations that enable you to perform a wide range of tasks, from combining sets to finding common elements, as well as updating and modifying sets based on other sets. By mastering these operations, you’ll gain the ability to work with sets dynamically, making it easier to solve various programming problems [Python Software Foundation, 2023].
Let’s explore these set operations in detail:
A.union(B)- Union of SetsAandB:This operation creates a new set that contains all the elements from both sets
AandB. In other words, it combines the elements of both sets while removing duplicates (since sets only contain unique elements).Equivalent:
A | BResult: The result is a new set containing all unique elements from sets
AandB.
Fig. 3.12 Illustrating the union of two sets A and B.#
Example:
# Creating set 'A' with elements {1, 2, 3}
A = {1, 2, 3}
# Creating set 'B' with elements {3, 4, 5}
B = {3, 4, 5}
# Creating a new set 'union_set' containing all unique elements from both 'A' and 'B'
union_set = A.union(B)
# Printing the 'union_set', which combines elements from both 'A' and 'B'
print(union_set)
{1, 2, 3, 4, 5}
A.intersection(B)- Intersection of SetsAandB:This operation creates a new set that contains only the elements that are common to both sets
AandB. It finds the intersection of the two sets.Equivalent:
A & BResult: The result is a new set containing elements that are present in both sets
AandB.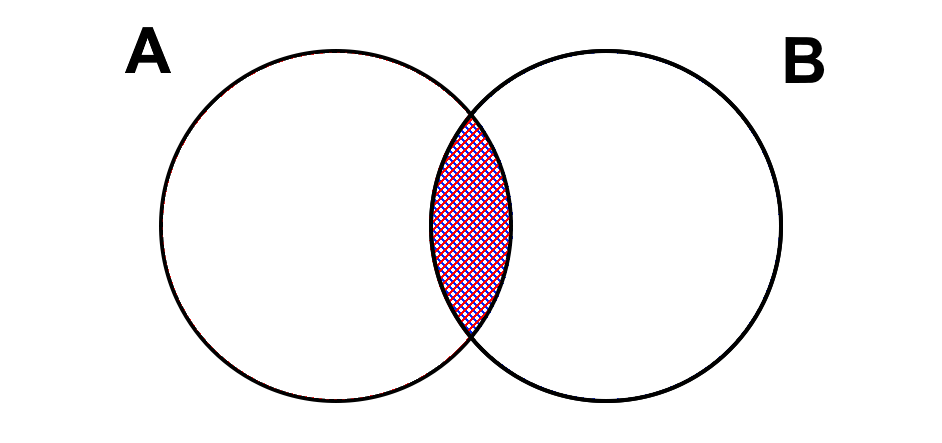
Fig. 3.13 Illustrating the intersection of two sets A and B.#
Example:
# Creating set 'A' with elements {1, 2, 3, 4}
A = {1, 2, 3, 4}
# Creating set 'B' with elements {3, 4, 5, 6}
B = {3, 4, 5, 6}
# Creating a new set 'intersection_set' containing elements that are common to both 'A' and 'B'
intersection_set = A.intersection(B)
# Printing the 'intersection_set', which includes the shared elements of 'A' and 'B'
print(intersection_set)
{3, 4}
A.difference(B)- Difference of SetsAandB:This operation creates a new set that contains the elements from set
Athat are not present in setB.Equivalent:
A - BResult: The result is a new set containing elements that are in set
Abut not in setB.
Fig. 3.14 Illustrating the set difference A - B.#
Example:
# Creating set 'A' with elements {1, 2, 3, 4}
A = {1, 2, 3, 4}
# Creating set 'B' with elements {3, 4, 5, 6}
B = {3, 4, 5, 6}
# Creating a new set 'difference_set' containing elements that are in 'A' but not in 'B'
difference_set = A.difference(B)
# Printing the 'difference_set', which includes elements unique to 'A' compared to 'B'
print(difference_set)
{1, 2}
A.symmetric_difference(B)- Symmetric Difference of SetsAandB:This operation creates a new set that contains the elements that are present in either set
Aor setB, but not in both.Equivalent:
A ^ BResult: The result is a new set containing elements that are unique to either set
Aor setB, but not present in both.
Fig. 3.15 Symmetric Difference of Sets A and B.#
Example:
# Creating set 'A' with elements {1, 2, 3, 4}
A = {1, 2, 3, 4}
# Creating set 'B' with elements {3, 4, 5, 6}
B = {3, 4, 5, 6}
# Creating a new set 'symmetric_difference_set' containing elements that are unique to either 'A' or 'B', but not both
symmetric_difference_set = A.symmetric_difference(B)
# Printing the 'symmetric_difference_set', which includes elements that are unique to either 'A' or 'B'
print(symmetric_difference_set)
{1, 2, 5, 6}
Note
Mathematically, the concept of symmetric difference can be formally expressed as:
Here, the symbol \(\setminus\) signifies the set difference operation, indicating the elements that are unique to each set when comparing sets A and B.
A.intersection_update(B)- Return setAkeeping only elements also found in setB:This operation modifies the set
Ato contain only the elements that are also present in setB. It computes the intersection of setsAandBand updatesAwith the result.Equivalent:
A &= BResult: The result is set
Aafter keeping only the elements that are common to both setsAandB.Example:
# Creating set 'A' with elements {1, 2, 3, 4}
A = {1, 2, 3, 4}
# Creating set 'B' with elements {3, 4, 5, 6}
B = {3, 4, 5, 6}
# Updating set 'A' in place to contain only elements that are common to both 'A' and 'B'
A.intersection_update(B)
# Printing the updated 'A', which now contains the intersection of 'A' and 'B'
print(A)
{3, 4}
A.difference_update(B)- Return setAafter removing elements found in setB:This operation modifies the set
Aby removing elements that are present in setB.Equivalent:
A -= BResult: The result is set
Aafter removing all elements found in setB.Example:
# Creating set 'A' with elements {1, 2, 3, 4}
A = {1, 2, 3, 4}
# Creating set 'B' with elements {3, 4, 5, 6}
B = {3, 4, 5, 6}
# Updating set 'A' in place to contain elements that are in 'A' but not in 'B'
A.difference_update(B)
# Printing the updated 'A', which now includes elements unique to 'A' compared to 'B'
print(A)
{1, 2}
A.symmetric_difference_update(B)- Return setAwith elements fromAorBbut not both:This operation modifies the set
Ato contain only the elements that are present in either setAor setB, but not in both.Equivalent:
A ^= BResult: The result is set
Aafter applying the symmetric difference operation with setB.Example:
# Creating set 'A' with elements {1, 2, 3, 4}
A = {1, 2, 3, 4}
# Creating set 'B' with elements {3, 4, 5, 6}
B = {3, 4, 5, 6}
# Updating set 'A' in place to contain elements that are unique to either 'A' or 'B', but not both
A.symmetric_difference_update(B)
# Printing the updated 'A', which now includes elements unique to either 'A' or 'B'
print(A)
{1, 2, 5, 6}
Operation |
Equivalent |
Result |
|---|---|---|
|
|
Create a new set with elements from both |
|
|
Create a new set with elements common to sets |
|
|
Create a new set with elements in set |
|
|
Create a new set with elements in either set |
|
|
Modify set |
|
|
Modify set |
|
|
Modify set |
3.5.7. Iterating Over a Set#
You can use a for loop to iterate over the elements in a set. Since sets are unordered, the order in which the elements are iterated may not be the same as the order in which you added them.
for item in my_set:
print(item)
3.5.8. Frozen Sets#
In addition to regular sets, Python also provides a type called “frozenset.” A frozenset is an immutable version of a set. This means once you create a frozenset, you cannot add or remove elements from it. However, you can use frozensets as elements of other sets or dictionaries, making them useful in situations where you need a hashable and immutable collection.
frozen = frozenset([1, 2, 3])
Here’s an explanation of the code:
frozenset(): This is a Python built-in function used to create a frozenset. Inside the parentheses, you provide the elements you want to include in the frozenset.[1, 2, 3]: This is a list containing three integer elements, namely 1, 2, and 3.frozenset([1, 2, 3]): This line of code creates a frozenset named ‘frozen’ and initializes it with the elements from the list, resulting in a frozenset that contains the values 1, 2, and 3.
The key characteristic of a frozenset is that it is immutable, which means you cannot add, remove, or modify elements in it after it has been created. This is in contrast to a regular set, which is mutable and allows you to modify its contents. Frozensets are useful in situations where you need an unchangeable set of elements, such as when you want to use a set as a key in a dictionary because regular sets cannot be used as dictionary keys due to their mutability.
