10.1. Fundamental Structure of Decision Trees

Decision trees are hierarchical models that represent a sequence of decisions, leading to predictions or classifications. They have a tree-like structure, where each node represents a decision or a prediction, and each branch represents an outcome of the decision. The tree starts at the top with the root node, which contains the entire dataset, and branches down, ending with leaf nodes, which contain the final predictions or classifications. This structure reflects a step-by-step process of answering questions or evaluating conditions to arrive at an outcome.

10.1.1. Root Nodes, Internal Nodes, and Leaf Nodes

A decision tree is composed of three types of nodes: root node, internal nodes, and leaf nodes. Each node represents a decision or a prediction based on the input features. The nodes are connected by branches, which represent the outcomes of the decisions. The structure of a decision tree reflects a step-by-step process of answering questions or evaluating conditions to arrive at an outcome.

Let’s go through the definitions and examples of these nodes:

1. Root Node: The root node is the starting point of the decision tree. It contains the entire dataset and poses the first question or condition to split the data into subsets. The root node sets the tone for the subsequent decisions and branches in the tree.

Example: In a medical diagnosis context, the root node could ask, “Is the patient’s temperature above 38°C?” Based on the answer, the data splits into two subsets: one with high temperature and another with normal temperature. This split forms the basis for the subsequent tree structure, where further questions are asked to narrow down the diagnosis.

2. Internal Nodes: Internal nodes are the decision points in the tree. They present questions or conditions about specific features to further split the data. They guide the data down different branches based on the answers or outcomes of the questions or conditions. Each internal node represents a feature and its associated condition, which determines the path that the data points will follow as they traverse the tree. Internal nodes play a crucial role in navigating through the decision-making process.

Example: Continuing with the medical diagnosis example, an internal node might ask, “Does the patient have a cough?” If the answer is “Yes,” the data proceeds down one branch, and if the answer is “No,” it goes down another. This split allows the model to consider various symptoms and their interactions in making an accurate diagnosis.

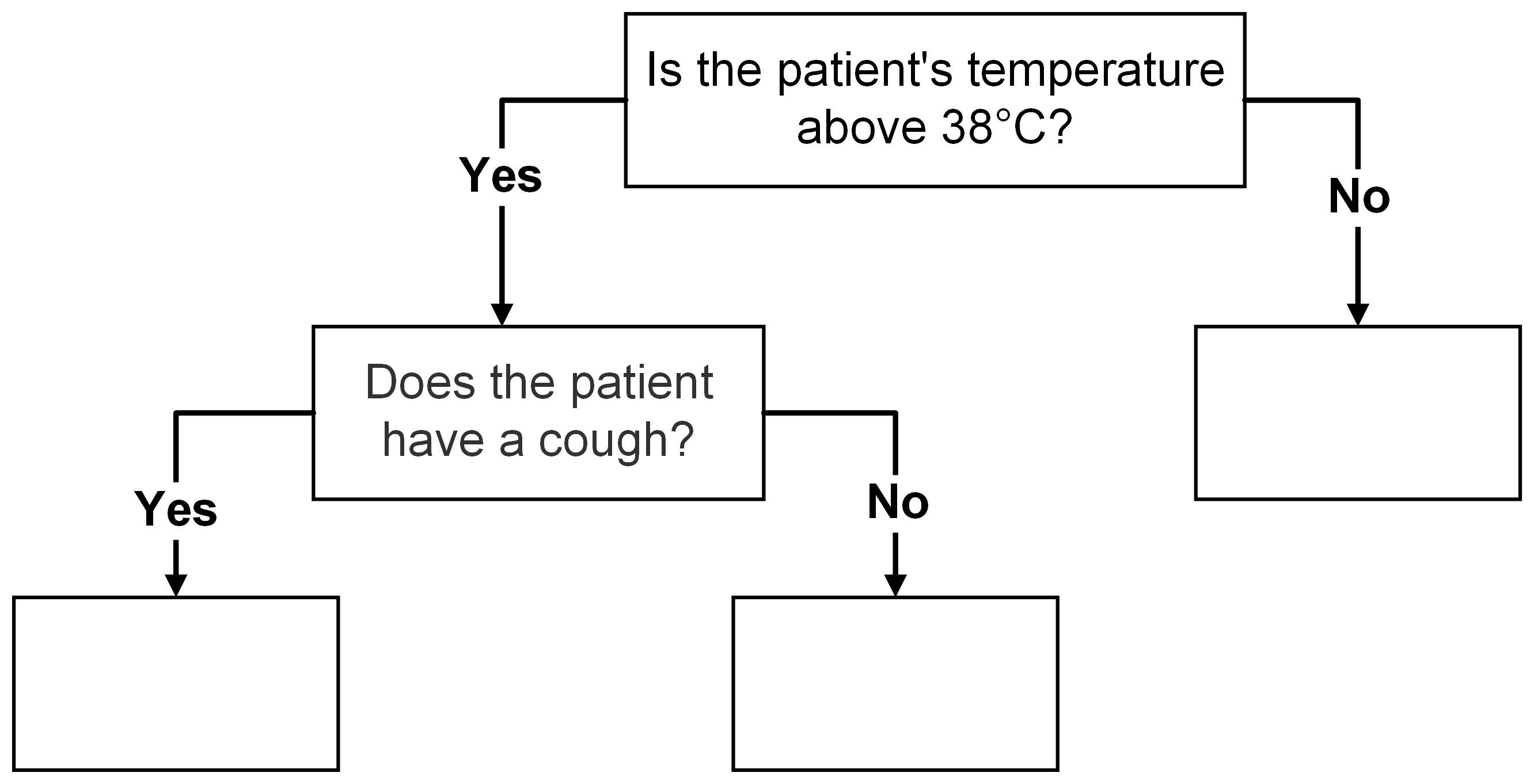
Fig. 10.1 An Example of Root Node and Internal Nodes

3. Leaf Nodes: Leaf nodes are the end points of the decision tree. They represent the final predictions or classifications that the tree makes. Each leaf node corresponds to a specific outcome, category, or numerical value. Once a data point reaches a leaf node, the prediction or classification associated with that leaf node becomes the final decision for that data point.

Example: As we progress in the medical diagnosis scenario, we arrive at the leaf nodes, which represent the final conclusions in the decision tree. For instance, a leaf node could correspond to the diagnosis ‘Common Cold’ if a patient’s symptoms match that specific outcome. Alternatively, another leaf node might correspond to the diagnosis ‘Influenza’ for a different set of symptoms. Each leaf node signifies a definitive decision or classification, and once a patient’s data reaches a leaf node, the corresponding diagnosis becomes the final determination for that case.

10.1.2. Popular tree-based methods

Tree-based methods are powerful and versatile techniques for supervised learning, both for classification and regression problems [James et al., 2023]. They use a hierarchical structure of splits to partition the feature space into regions, and then assign a class label or a numerical value to each region. Some splits may be binary, where each split is based on a single feature and a threshold value, or non-binary, where each split is based on a linear combination of features or a non-linear function. Some of the most widely used tree-based methods are:

• Decision trees: They are the simplest form of tree-based methods, where each split is based on a criterion, which can be entropy, Gini index, misclassification rate, information gain, chi-square test, or permutation test, depending on the parameter criterion. The criterion determines the best feature and threshold for each split. Decision trees are easy to interpret and visualize, but they tend to overfit the data and have high variance.

• Random forests: They are an ensemble method that combines many decision trees, each trained on a bootstrap sample of the data and features. A bootstrap sample is a random sample drawn with replacement from the original data. The final prediction is obtained by averaging the predictions of the individual trees for regression problems, or by majority voting for classification problems. Random forests reduce the variance and overfitting of decision trees, and improve their accuracy and robustness.

• Boosting: They are another ensemble method that iteratively fits decision trees to the pseudo-residuals of the previous trees, and combines them with weights to form a strong learner. The pseudo-residuals are the negative gradient of the loss function with respect to the predictions. Boosting algorithms, such as AdaBoost or gradient boosting, can achieve high accuracy and performance, but they are more prone to overfitting and require careful tuning of the parameters.

Scikit-Learn (sklearn) is a popular Python library that offers an array of robust and efficient methods for building classification and regression trees, each tailored to specific tasks and data complexities [scikit-learn Developers, 2023]. Sklearn provides a consistent and user-friendly interface for creating, fitting, and evaluating tree-based models, as well as tools for feature selection, preprocessing, and visualization.

Examples of Classification Tree Methods

The following are some examples of classification tree methods available in sklearn [scikit-learn Developers, 2023]:

1. DecisionTreeClassifier: This class implements the CART algorithm to build classification trees. It uses a criterion, which can be Gini impurity, entropy, misclassification rate, or information gain, depending on the parameter criterion. The criterion determines the best feature and threshold for each split. You can control the complexity and size of the tree by tuning parameters such as max_depth and min_samples_split [Gallatin and Albon, 2023, scikit-learn Developers, 2023].

2. RandomForestClassifier: This class combines multiple decision trees, each trained on a bootstrap sample of the data and features, and averages their predictions. A bootstrap sample is a random sample drawn with replacement from the original data. This reduces the variance and overfitting of single trees, and improves the accuracy and robustness of the model [Géron, 2022, scikit-learn Developers, 2023].

3. GradientBoostingClassifier: This class applies the gradient boosting technique to classification problems. It sequentially fits decision trees to the pseudo-residuals of the previous trees, and adjusts their weights to form a strong learner. The pseudo-residuals are the negative gradient of the loss function with respect to the predictions. This allows the model to capture complex nonlinear relationships in the data, but it also requires careful tuning of the parameters and may overfit the data [scikit-learn Developers, 2023].

4. AdaBoostClassifier: This class uses the adaptive boosting algorithm to combine several weak classifiers, usually decision trees, into a powerful classification model. It increases the sample weights of the misclassified instances, and focuses the learning on the difficult cases. The sample weights are used to modify the contribution of each instance to the loss function. This enhances the accuracy and performance of the model, but it may also be sensitive to noise and outliers [scikit-learn Developers, 2023].

Examples of Regression Tree Methods

The following are some examples of regression tree methods available in sklearn [scikit-learn Developers, 2023]:

1. DecisionTreeRegressor: This class uses the CART algorithm to construct regression trees. It splits the feature space based on a criterion, which can be mean squared error, mean absolute error, or median absolute error, depending on the parameter criterion. The criterion determines the optimal feature and threshold for each split. DecisionTreeRegressor can produce accurate and interpretable predictions, but it may also overfit the data and have high variance [scikit-learn Developers, 2023].

2. RandomForestRegressor: This class combines many regression trees, each trained on a random subset of the data and features, and averages their predictions. This reduces the variance and overfitting of single trees, and improves the accuracy and robustness of the model. RandomForestRegressor can handle complex and nonlinear relationships in the data, but it may require the data to be complete and do not handle missing values internally [scikit-learn Developers, 2023].

3. GradientBoostingRegressor: This class applies the gradient boosting technique to regression problems. It sequentially fits regression trees to the pseudo-residuals of the previous trees, and adjusts their weights to form a strong learner. The pseudo-residuals are the negative gradient of the loss function with respect to the predictions. GradientBoostingRegressor can achieve high accuracy and performance, but it also requires careful tuning of the parameters and may overfit the data [scikit-learn Developers, 2023].

4. AdaBoostRegressor: This class uses the adaptive boosting algorithm to combine several weak regression models, usually decision trees, into a powerful predictor. It increases the sample weights of the data points with high prediction errors, and focuses the learning on the difficult cases. The sample weights are used to modify the contribution of each data point to the loss function. AdaBoostRegressor can enhance the accuracy and performance of the model, but it may also be sensitive to noise and outliers [scikit-learn Developers, 2023].

10.1.3. Advantages and Disadvantages of Decision Trees

Decision Trees (DTs) are a type of machine learning technique that can be used for both classification and regression tasks. They work by building a tree-like model where each internal node represents a test on an input feature, and each leaf node represents a predicted value or class. Decision trees aim to create simple and interpretable decision rules from the data, and they can approximate complex and nonlinear relationships using piecewise constant functions [James et al., 2023, scikit-learn Developers, 2023].

10.1.3.1. Advantages of Decision Trees:

• Interpretability: Decision trees are easy to understand and explain, and their structure can be visualized using diagrams or graphs.

• Minimal Data Preparation: Decision trees do not require much data preprocessing, such as normalization, dummy encoding, or missing value imputation. However, some implementations, such as scikit-learn’s, may have some limitations for categorical features or incomplete data.

• Efficiency: Decision trees are fast to train and predict, as the cost grows logarithmically with the size of the data.

• Handling of Mixed Data: Decision trees can handle both numerical and categorical features, although some implementations, such as scikit-learn’s, may have some limitations for categorical features.

• Multi-output Support: Decision trees can deal with problems that have multiple target variables, such as multi-label classification or multi-variate regression.

• White Box Model: Decision trees are transparent and provide clear explanations for their predictions, unlike “black box” models such as neural networks.

• Robustness: Decision trees can perform well even when the model assumptions are not exactly met by the data-generating process.

10.1.3.2. Disadvantages of Decision Trees:

• Overfitting: Decision trees can fit the training data too closely, leading to poor generalization and high variance. Pruning and limiting the tree depth are some methods to prevent overfitting.

• Instability: Decision trees can be sensitive to small changes in the data, resulting in different and inconsistent models. Ensemble methods, such as random forests, can reduce this instability by averaging over many trees.

• Discontinuity: Decision trees make predictions using step functions, which are discontinuous and have jumps or breaks in their graph. This makes them unsuitable for extrapolation or interpolation.

• Computational Complexity: Finding the optimal decision tree is a NP-hard problem, meaning that it is computationally intractable. Practical algorithms use heuristics, such as greedy search, to find locally optimal solutions. Ensemble methods can also overcome this complexity by combining simpler trees.

• Difficulty with Complex Concepts: Decision trees may struggle to learn complex logical concepts, such as XOR, parity, or multiplexer, that require a large number of splits or nodes.

• Bias in Imbalanced Data: Decision trees may produce biased models when the data is imbalanced, meaning that some classes are overrepresented or underrepresented. Balancing the data before training, such as using resampling or weighting, can mitigate this bias.