TensorFlow Basics

12.3. TensorFlow Basics#

Deep learning is a powerful field of artificial intelligence that uses neural networks to make sense of data and perform tasks like recognizing images, understanding natural language, and generating speech. These neural networks consist of intricate layers of nodes that perform complex calculations on data inputs and outputs. To efficiently handle this data and speed up these calculations, deep learning relies on a special data structure called tensors.

Tensors can be thought of as a more advanced version of the familiar arrays we often use in programming and mathematics. Arrays are collections of elements organized in rows and columns, and tensors share a strong connection with them. Let’s explore how they are similar [TensorFlow Developers, 2023]:

12.3.1. Array and Tensor Connection#

Multidimensional Flexibility: Arrays, with their ability to have multiple dimensions, lay the foundation for tensors. In arrays, dimensions are like the arrangement of data in a musical score, with rows and columns. Tensors take this idea further, extending dimensions into a multi-axis arrangement that can adapt to any kind of data structure.
Indexing and Access: Just like you use indices to access elements in arrays, tensors work the same way for retrieving data. Elements inside both arrays and tensors are accessed and manipulated using indices, making data handling consistent.
Mathematical Aptitude: Arrays have a well-established reputation for their mathematical capabilities, crucial for performing various operations. Tensors, as their successors, continue this mathematical legacy, serving as the conduits through which deep learning networks perform complex numerical operations.
Data Representation: Similar to how arrays are used to represent data, tensors take center stage in deep learning. They excel at accurately encapsulating data, whether it’s images, text, or sound. These versatile data structures channel the essence of information into the neural network’s computational fabric.
Transformations and Operations: Both arrays and tensors are alike in their transformative nature. They gracefully adapt within their dimensions to accommodate a range of mathematical operations, such as addition, multiplication, and transformation. Just as arrays change during calculations, tensors efficiently absorb operations, enhancing the capabilities of neural networks.

12.3.2. Strong Ties to NumPy Arrays#

While tensors may seem like a novel concept in the context of deep learning, it’s important to recognize their strong connection to arrays, which have long been fundamental in programming and mathematics. Arrays can be seen as simplified versions of tensors, often with fixed dimensions and data types. Tensors, on the other hand, are more flexible and dynamic, allowing for variable dimensions and data types. Tensors also have some additional features and functionalities that make them more suitable for deep learning, such as automatic differentiation, GPU support, and distributed training. However, tensors and arrays are still compatible and interchangeable, thanks to the NumPy library, which provides a common interface for both data structures. NumPy is a popular Python library that offers a variety of tools and functions for working with arrays and tensors. It allows you to easily create, manipulate, and convert arrays and tensors, as well as perform various mathematical and statistical operations on them. NumPy is widely used in scientific computing and data analysis, and it serves as the backbone of many other libraries and frameworks, including TensorFlow. TensorFlow is a leading deep learning framework that provides a comprehensive set of tools and features for building, training, and deploying neural networks. TensorFlow uses tensors as its main data structure, and it relies on NumPy for creating and converting tensors from and to arrays. This makes it easy to integrate TensorFlow with other libraries and frameworks that use arrays, such as Pandas, Scikit-learn, and Matplotlib. By using NumPy and TensorFlow together, you can leverage the power and flexibility of tensors, while also benefiting from the simplicity and familiarity of arrays [Prakash and Kanagachidambaresan, 2021].

import tensorflow as tf
import numpy as np

Definition

Tensors are specialized data structures that resemble multi-dimensional arrays, but with some key differences and advantages. Tensors have the following characteristics [TensorFlow Developers, 2023]:

They have a consistent data type, which is referred to as a ‘dtype.’ The available data types can be found in tf.dtypes.DType.
They are immutable, which means that you cannot modify the content of an existing tensor; instead, you create a new tensor when changes are needed. This is similar to how Python treats numbers and strings.
They can have variable dimensions and data types, which makes them more flexible and dynamic than arrays.
They have additional features and functionalities that make them more suitable for deep learning, such as automatic differentiation, GPU support, and distributed training.

Tensors are the main data structure used by TensorFlow, a leading deep learning framework that provides a comprehensive set of tools and features for building, training, and deploying neural networks.

Let’s begin our journey into the world of TensorFlow by learning how to create basic tensors. Tensors are the fundamental data structures of TensorFlow, enabling us to work with data in a powerful and flexible way [TensorFlow Developers, 2023].

12.3.3. Scalar or Rank-0 Tensor#

A scalar or rank-0 tensor is a special type of tensor that holds a single value and has no dimensions or axes [TensorFlow Developers, 2023]. It is the simplest form of a tensor, and it can be used to represent constants, such as numbers or strings.

# Import TensorFlow
import tensorflow as tf

def print_bold(txt, c=31):
    """
    Display text in bold with optional color.

    Parameters:
    - txt (str): The text to be displayed.
    - c (int): Color code for the text (default is 31 for red).
    """
    print(f"\033[1;{c}m" + txt + "\033[0m")

# Creating a Rank-0 Tensor (Scalar) with an Integer value
# By default, this will be an int32 tensor; more on "dtypes" below.
rank_0_tensor = tf.constant(680)

# Displaying the Rank-0 Tensor
print_bold("Rank-0 Tensor (Scalar) with Integer value:", 32)
print(rank_0_tensor)

# Creating a Rank-0 Tensor (Scalar) with a Boolean value
# This will be a bool tensor with a specified dtype.
rank_0_tensor_bool = tf.constant(True, dtype=tf.bool)

# Displaying the Rank-0 Tensor
print_bold("\nRank-0 Tensor (Scalar) with Boolean value:", 32)
print(rank_0_tensor_bool)

# Creating a Rank-0 Tensor (Scalar) with a String value
# This will be a string tensor with a specified dtype.
rank_0_tensor_string = tf.constant("Hello, ENGG 680!", dtype=tf.string)

# Displaying the Rank-0 Tensor
print_bold("\nRank-0 Tensor (Scalar) with String value:", 32)
print(rank_0_tensor_string)

# Creating a Rank-0 Tensor (Scalar) with a Float value
# This will be a float64 tensor with a specified dtype.
rank_0_tensor_float = tf.constant(3.14159, dtype=tf.float64)

# Displaying the Rank-0 Tensor
print_bold("\nRank-0 Tensor (Scalar) with Float value:", 32)
print(rank_0_tensor_float)

Rank-0 Tensor (Scalar) with Integer value:
tf.Tensor(680, shape=(), dtype=int32)

Rank-0 Tensor (Scalar) with Boolean value:
tf.Tensor(True, shape=(), dtype=bool)

Rank-0 Tensor (Scalar) with String value:
tf.Tensor(b'Hello, ENGG 680!', shape=(), dtype=string)

Rank-0 Tensor (Scalar) with Float value:
tf.Tensor(3.14159, shape=(), dtype=float64)

../_images/scalar.png — Fig. 12.5 Tensors with a scalar nature and a shape represented as an empty set of parentheses ().#

12.3.4. Vector or Rank-1 Tensor#

A vector or rank-1 tensor is a tensor that has only one dimension or axis. It can be seen as a sequence of values, similar to a list, that has a specific direction. For example, a vector can represent the coordinates of a point in a two-dimensional plane, or the velocity of an object in a three-dimensional space [TensorFlow Developers, 2023].

# Import TensorFlow
import tensorflow as tf

def print_bold(txt, c=31):
    """
    Display text in bold with optional color.

    Parameters:
    - txt (str): The text to be displayed.
    - c (int): Color code for the text (default is 31 for red).
    """
    print(f"\033[1;{c}m" + txt + "\033[0m")

# Creating a Rank-1 Tensor (Vector) with integer values
# We specify float values to make it a float tensor.
rank_1_tensor = tf.constant([1, 2, 3, 4])

# Displaying the Rank-1 Tensor
print_bold("Rank-1 Tensor (Vector) with Integer values:")
print(rank_1_tensor)

# Creating a Rank-1 Tensor (Vector) with string values
# We specify string values to make it a string tensor.
rank_1_tensor = tf.constant(["Hello", "ENGG", "680"])

# Displaying the Rank-1 Tensor
print_bold("\nRank-1 Tensor (Vector) with String values:")
print(rank_1_tensor)

# Creating a Rank-1 Tensor (Vector) with boolean values
# We specify boolean values to make it a boolean tensor.
rank_1_tensor = tf.constant([True, False, True])

# Displaying the Rank-1 Tensor
print_bold("\nRank-1 Tensor (Vector) with Boolean values:")
print(rank_1_tensor)

# Creating a Rank-1 Tensor (Vector) with complex values
# We specify complex values to make it a complex tensor.
rank_1_tensor = tf.constant([1 + 2j, 3 - 4j, 5 + 6j])

# Displaying the Rank-1 Tensor
print_bold("\nRank-1 Tensor (Vector) with Complex values:")
print(rank_1_tensor)

Rank-1 Tensor (Vector) with Integer values:
tf.Tensor([1 2 3 4], shape=(4,), dtype=int32)

Rank-1 Tensor (Vector) with String values:
tf.Tensor([b'Hello' b'ENGG' b'680'], shape=(3,), dtype=string)

Rank-1 Tensor (Vector) with Boolean values:
tf.Tensor([ True False  True], shape=(3,), dtype=bool)

Rank-1 Tensor (Vector) with Complex values:
tf.Tensor([1.+2.j 3.-4.j 5.+6.j], shape=(3,), dtype=complex128)

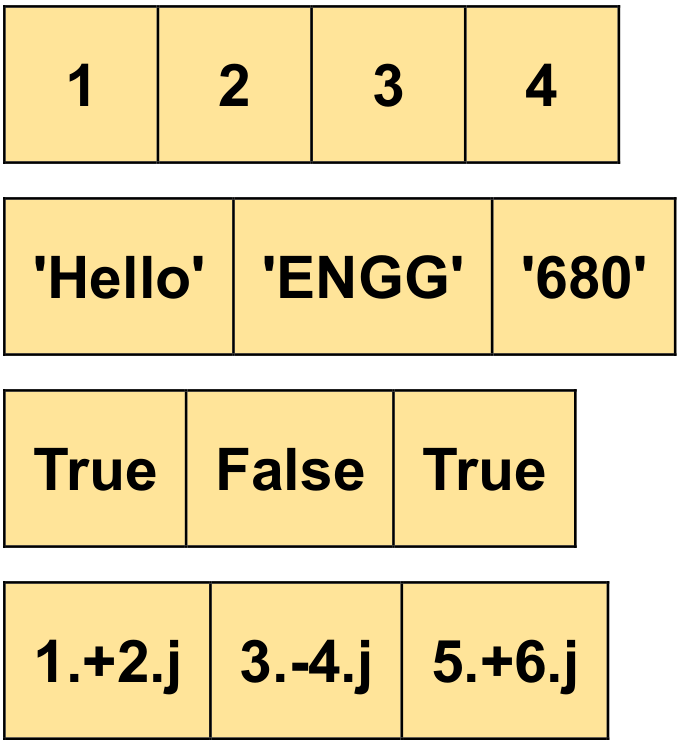
../_images/vector.png — Fig. 12.6 Tensors with a shape of 3 in the context of vector notation.#

12.3.5. Matrix or Rank-2 Tensor#

A matrix or rank-2 tensor is a tensor that has two dimensions or axes. It can be seen as a grid of values, similar to a two-dimensional array, that has a specific row and column structure. For example, a matrix can represent the pixels of an image, the coefficients of a linear system, or the features of a data set [TensorFlow Developers, 2023].

# Import TensorFlow
import tensorflow as tf

# Creating a Rank-2 Tensor (Matrix) with Specific Dtype
# We define a 2x2 matrix and set the data type to float16.
rank_2_tensor = tf.constant([[11, 22],
                             [33, 44],
                             [55, 66]], dtype=tf.int16)

# Displaying the Rank-2 Tensor
print_bold("Rank-2 Tensor (Matrix) with Specific Dtype:")
print(rank_2_tensor)

Rank-2 Tensor (Matrix) with Specific Dtype:
tf.Tensor(
[[11 22]
 [33 44]
 [55 66]], shape=(3, 2), dtype=int16)

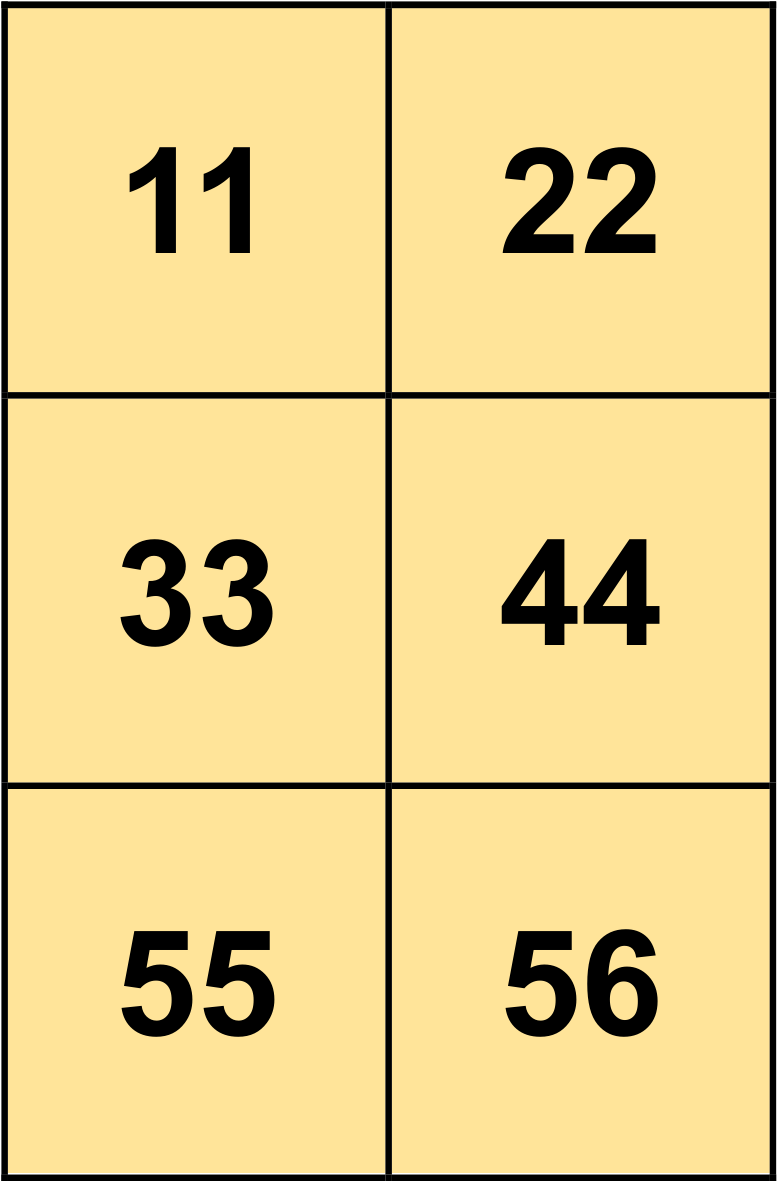
../_images/matrix.png — Fig. 12.7 A matrix with a shape of (3, 2).#

One way to create rank-2 tensors or matrices in TensorFlow is to use the built-in functions that generate tensors with specific values. In this example, we will see how to create rank-2 tensors with random values, zeros, and ones using tf.random.uniform, tf.zeros, and tf.ones respectively. These functions take a shape argument that specifies the number of rows and columns of the matrix. For example, shape=(3, 3) means a 3x3 matrix. We can then display the rank-2 tensors using the print function. Here is the code for this example:

# Creating a Rank-2 Tensor (Matrix) with Random Values
# We use tf.random.uniform to generate a 3x3 matrix with values between 0 and 1.
rank_2_tensor_random = tf.random.uniform(shape=(3, 3))

# Displaying the Rank-2 Tensor
print_bold("Rank-2 Tensor (Matrix) with Random Values:")
print(rank_2_tensor_random)

# Creating a Rank-2 Tensor (Matrix) with Zeros
# We use tf.zeros to create a 4x4 matrix with all zeros.
rank_2_tensor_zeros = tf.zeros(shape=(4, 4))

# Displaying the Rank-2 Tensor
print_bold("\nRank-2 Tensor (Matrix) with Zeros:")
print(rank_2_tensor_zeros)

# Creating a Rank-2 Tensor (Matrix) with Ones
# We use tf.ones to create a 5x5 matrix with all ones.
rank_2_tensor_ones = tf.ones(shape=(5, 5))

# Displaying the Rank-2 Tensor
print_bold("\nRank-2 Tensor (Matrix) with Ones:")
print(rank_2_tensor_ones)

Rank-2 Tensor (Matrix) with Random Values:
tf.Tensor(
[[0.8024781  0.70768654 0.7383542 ]
 [0.16242695 0.703591   0.7325984 ]
 [0.7425693  0.40302432 0.04241037]], shape=(3, 3), dtype=float32)

Rank-2 Tensor (Matrix) with Zeros:
tf.Tensor(
[[0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]], shape=(4, 4), dtype=float32)

Rank-2 Tensor (Matrix) with Ones:
tf.Tensor(
[[1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]], shape=(5, 5), dtype=float32)

Tensors Can Have More Axes: Here’s an Example with Three Axes [TensorFlow Developers, 2023]:

# Creating a Rank-3 Tensor with Three Axes
# Here, we have a 3x2 grid of values, and
# there's an outer dimension encompassing them.
rank_3_tensor = tf.constant([[[11, 12, 13, 14], [15, 16, 17, 18]],
                             [[21, 22, 23, 24], [25, 26, 27, 28]],
                             [[31, 32, 33, 34], [35, 36, 37, 38]],
                             ])

# Displaying the Rank-3 Tensor
print_bold("Rank-3 Tensor with Three Axes:")
print(rank_3_tensor)

Rank-3 Tensor with Three Axes:
tf.Tensor(
[[[11 12 13 14]
  [15 16 17 18]]

 [[21 22 23 24]
  [25 26 27 28]]

 [[31 32 33 34]
  [35 36 37 38]]], shape=(3, 2, 4), dtype=int32)

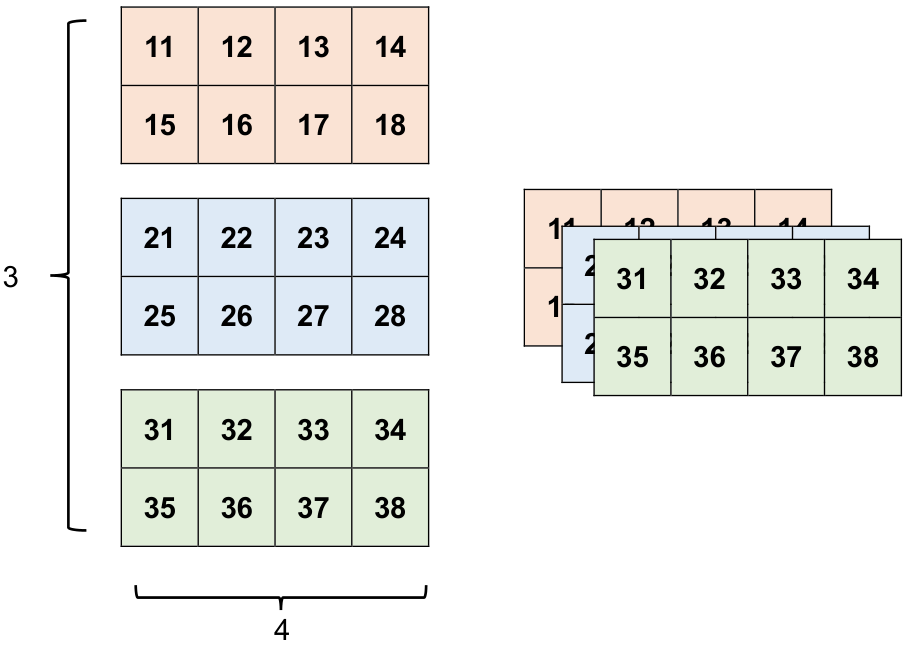
../_images/3d_tensor.png — Fig. 12.8 Visualizing the above 3D Tensor.#

12.3.6. Converting Tensors to NumPy Arrays#

TensorFlow and NumPy are both libraries for scientific computing in Python that provide powerful array objects to store and manipulate multidimensional data. They have some similarities, such as:

They both support various data types, such as int16, float32, bool, etc. In this example, we specify the data type of the tensor as int16 using the dtype argument [TensorFlow Developers, 2023] [Ramsundar and Zadeh, 2018] .
They both have similar methods to create arrays with specific values, such as tf.ones, tf.zeros, np.ones, np.zeros, etc. In this example, we use tf.constant to create a tensor with constant values [TensorFlow Developers, 2023] [Ramsundar and Zadeh, 2018] .
They both have similar attributes to access the shape and size of the arrays, such as tensor.shape, numpy_array.shape, tensor.size, numpy_array.size, etc. In this example, we print the shape of the tensor and the NumPy arrays using the shape attribute [TensorFlow Developers, 2023] [Ramsundar and Zadeh, 2018] .
They both have similar methods to perform mathematical operations on the arrays, such as tf.add, tf.multiply, np.add, np.multiply, etc. In this example, we do not perform any operations, but we could do so if we wanted to [TensorFlow Developers, 2023] [Ramsundar and Zadeh, 2018] .

However, they also have some differences, such as:

TensorFlow tensors are immutable, meaning that they cannot be modified once created. NumPy arrays are mutable, meaning that they can be modified in place. In this example, we cannot change the values of the tensor, but we can change the values of the NumPy arrays [TensorFlow Developers, 2023] [Ramsundar and Zadeh, 2018] .
TensorFlow tensors can be used to build and run computational graphs that can perform automatic differentiation and optimization for machine learning models [Géron, 2022] . NumPy arrays do not have this capability, and are mainly used for numerical analysis and data manipulation. In this example, we do not use any computational graphs, but we could do so if we wanted to build a machine learning model using TensorFlow [Abadi, 2016].
TensorFlow tensors can be executed on different devices, such as CPUs, GPUs, or TPUs, to accelerate the computation [Abadi, 2016]. NumPy arrays can only be executed on CPUs, and do not support parallelization or distribution. In this example, we do not specify any device, but we could do so if we wanted to use a different device for the tensor computation [TensorFlow Developers, 2023] [Ramsundar and Zadeh, 2018] .

To illustrate how to convert tensors to NumPy arrays, we will use the following code snippet:

# Import NumPy and TensorFlow
import numpy as np
import tensorflow as tf
from pprint import pprint

def print_bold(txt, c=31):
    """
    Display text in bold with optional color.

    Parameters:
    - txt (str): The text to be displayed.
    - c (int): Color code for the text (default is 31 for red).
    """
    print(f"\033[1;{c}m" + txt + "\033[0m")

# Create a 2D array of shape (2, 3) with random values
np_array = np.random.randint(0, 9, size=(2, 3))
print_bold("NumPy array:")
pprint(np_array)

# Convert the NumPy array to a TensorFlow tensor
tf_tensor = tf.convert_to_tensor(np_array)
print_bold("\nTensorFlow tensor:")
pprint(tf_tensor)

# Perform element-wise operations on both the array and the tensor
np_array = np_array + 1  # Add 1 to each element
tf_tensor = tf_tensor + 1  # Add 1 to each element
print_bold("\nNumPy array after adding 1:")
pprint(np_array)
print_bold("\nTensorFlow tensor after adding 1:")
pprint(tf_tensor)

np_array = np_array * 2  # Multiply each element by 2
tf_tensor = tf_tensor * 2  # Multiply each element by 2
print_bold("\nNumPy array after multiplying by 2:")
pprint(np_array)

print_bold("\nTensorFlow tensor after multiplying by 2:")
pprint(tf_tensor)

# Convert the TensorFlow tensor back to a NumPy array
np_array2 = tf_tensor.numpy()
print_bold("\nNumPy array converted from TensorFlow tensor:")
pprint(np_array2)

NumPy array:
array([[0, 6, 5],
       [4, 2, 3]])

TensorFlow tensor:
<tf.Tensor: shape=(2, 3), dtype=int32, numpy=
array([[0, 6, 5],
       [4, 2, 3]])>

NumPy array after adding 1:
array([[1, 7, 6],
       [5, 3, 4]])

TensorFlow tensor after adding 1:
<tf.Tensor: shape=(2, 3), dtype=int32, numpy=
array([[1, 7, 6],
       [5, 3, 4]])>

NumPy array after multiplying by 2:
array([[ 2, 14, 12],
       [10,  6,  8]])

TensorFlow tensor after multiplying by 2:
<tf.Tensor: shape=(2, 3), dtype=int32, numpy=
array([[ 2, 14, 12],
       [10,  6,  8]])>

NumPy array converted from TensorFlow tensor:
array([[ 2, 14, 12],
       [10,  6,  8]])

Example: In this example, we demonstrate that tensors are immutable.

# Import NumPy and TensorFlow
import numpy as np
import tensorflow as tf

# Create a 2D tensor of shape (2, 3) with constant values and int16 data type
tensor = tf.constant([[1, 2, 3], [4, 5, 6]], dtype=tf.int16)
print("TensorFlow tensor:\n", tensor)

# Convert the tensor to a NumPy array using the tensor.numpy method
array = tensor.numpy()
print("NumPy array converted from TensorFlow tensor:\n", array)

# Try to modify the first element of the first row of both the array and the tensor
array[0, 0] = 100 # This works, as NumPy arrays are mutable
tensor[0, 0] = 100 # This fails, as TensorFlow tensors are immutable

The output of this code is:

TensorFlow tensor:
 tf.Tensor(
[[1 2 3]
 [4 5 6]], shape=(2, 3), dtype=int16)
NumPy array converted from TensorFlow tensor:
 [[1 2 3]
 [4 5 6]]
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[30], line 12
     11 array[0, 0] = 100 # This works, as NumPy arrays are mutable
---> 12 tensor[0, 0] = 100 # This fails, as TensorFlow tensors are immutable

TypeError: 'tensorflow.python.framework.ops.EagerTensor' object does not support item assignment

As you can see, the NumPy array can be modified in place, but the TensorFlow tensor cannot. This is because TensorFlow tensors are immutable, meaning that they cannot be changed once created [TensorFlow Developers, 2023]. This is a design choice that allows TensorFlow to optimize the computation and memory usage of tensors, especially when they are used in computational graphs. If you want to change the values of a tensor, you need to create a new tensor with the updated values. For example, you can use the tf.assign function to assign new values to a variable that holds a tensor [TensorFlow Developers, 2023] . Here is an example of how to do that:

# Import TensorFlow
import tensorflow as tf

# Create a variable that holds a 2D tensor of shape (2, 3) with constant values and int16 data type
var = tf.Variable([[1, 2, 3], [4, 5, 6]], dtype=tf.int16)
print_bold("TensorFlow Variable:")
print(var)

# Try to modify the first element of the first row of the variable using the tf.assign function
var[0, 0].assign(100)  # This works, as variables can be updated using the assign method
print_bold("\nTensorFlow Variable after assigning 100 to the first element of the first row:")
print(var)

TensorFlow Variable:
<tf.Variable 'Variable:0' shape=(2, 3) dtype=int16, numpy=
array([[1, 2, 3],
       [4, 5, 6]], dtype=int16)>

TensorFlow Variable after assigning 100 to the first element of the first row:
<tf.Variable 'Variable:0' shape=(2, 3) dtype=int16, numpy=
array([[100,   2,   3],
       [  4,   5,   6]], dtype=int16)>

As you can see, the variable can be updated using the assign method, which creates a new tensor with the updated values and assigns it to the variable. This is different from modifying the tensor directly, which is not possible. This example demonstrates how to update the values of a tensor using the tf.assign function [TensorFlow Developers, 2023].

12.3.7. Data Types in TensorFlow#

To examine the data type of a tf.Tensor, you can utilize the Tensor.dtype property. When generating a tf.Tensor from a Python object, you have the option to specify the data type if desired [TensorFlow Developers, 2023].

In cases where you don’t specify a data type, TensorFlow automatically selects an appropriate one to accommodate your data. For instance, TensorFlow converts Python integers to tf.int32 and Python floating-point numbers to tf.float32. In other scenarios, TensorFlow applies the same conventions as NumPy does when converting to arrays [TensorFlow Developers, 2023].

Moreover, TensorFlow permits you to perform type casting, enabling you to switch between different data types as needed.

# Import TensorFlow
import tensorflow as tf

# Create a tensor with float64 data type
the_f64_tensor = tf.constant([2.2, 3.3, 4.4], dtype=tf.float64)
print_bold("Original Float64 Tensor:")
print(the_f64_tensor)

# Cast the float64 tensor to float16
the_f16_tensor = tf.cast(the_f64_tensor, dtype=tf.float16)
print_bold("\nFloat64 Tensor cast to Float16:")
print(the_f16_tensor)

# Cast the float16 tensor to uint8 (unsigned 8-bit integer)
# This will lead to loss of decimal precision
the_u8_tensor = tf.cast(the_f16_tensor, dtype=tf.uint8)
print_bold("\nFloat16 Tensor cast to Uint8:")
print(the_u8_tensor)

Original Float64 Tensor:
tf.Tensor([2.2 3.3 4.4], shape=(3,), dtype=float64)

Float64 Tensor cast to Float16:
tf.Tensor([2.2 3.3 4.4], shape=(3,), dtype=float16)

Float16 Tensor cast to Uint8:
tf.Tensor([2 3 4], shape=(3,), dtype=uint8)

12.3.8. Broadcasting#

Broadcasting is a concept adopted from the equivalent feature in NumPy. In essence, broadcasting enables smaller tensors to be automatically expanded to match the dimensions of larger tensors when performing combined operations on them [TensorFlow Developers, 2023].

The most straightforward and frequent scenario occurs when you try to multiply or add a tensor by a scalar value. In this instance, the scalar value is broadcasted, causing it to take on the same shape as the other tensor in the operation. This seamless extension of dimensions facilitates efficient computation of operations involving tensors with varying shapes [TensorFlow Developers, 2023].

# Import TensorFlow
import tensorflow as tf

# Define a constant tensor
x = tf.constant([1, 2, 3])
print_bold("Original Tensor:")
print(x)

# Define scalar and tensor constants
y = tf.constant(2)
z = tf.constant([2, 2, 2])

# Perform the same computation using different expressions
result1 = tf.multiply(x, 2)  # Broadcasting scalar to tensor
result2 = x * y  # Broadcasting scalar to tensor using operator
result3 = x * z  # Broadcasting tensor to tensor

# Print the results
print_bold("\nResult 1 (Scalar Broadcasting):")
print(result1)
print_bold("\nResult 2 (Scalar Broadcasting using Operator):")
print(result2)
print_bold("\nResult 3 (Tensor Broadcasting):")
print(result3)

Original Tensor:
tf.Tensor([1 2 3], shape=(3,), dtype=int32)

Result 1 (Scalar Broadcasting):
tf.Tensor([2 4 6], shape=(3,), dtype=int32)

Result 2 (Scalar Broadcasting using Operator):
tf.Tensor([2 4 6], shape=(3,), dtype=int32)

Result 3 (Tensor Broadcasting):
tf.Tensor([2 4 6], shape=(3,), dtype=int32)

Similarly, axes with a length of 1 can be extended to align with the dimensions of other arguments during operations. This extension can be applied to both operands simultaneously within a single computation [TensorFlow Developers, 2023].

In the example, a 3x1 matrix is multiplied element-wise with a 1x4 matrix, resulting in a 3x4 matrix. It’s worth noting that the leading 1 in the matrix dimensions is not strictly required. For instance, the shape of matrix y can be expressed as [4], highlighting that broadcasting effectively accounts for dimensions of length 1, regardless of whether they are explicitly stated [TensorFlow Developers, 2023].

# Import TensorFlow
import tensorflow as tf

# Define a tensor
x = tf.constant([1, 2, 3, 4, 5])
print_bold("Original Tensor:")
print(x)
x = tf.reshape(x, [5, 1])
print_bold("\nReshaped x:")
print(x)

# Create a tensor with values ranging from 1 to 4
y = tf.range(1, 5)
print_bold("\ny:")
print(y)

# Perform element-wise multiplication using broadcasting
result = tf.multiply(x, y)
print_bold("Result of Element-wise Multiplication:")
print(result)

Original Tensor:
tf.Tensor([1 2 3 4 5], shape=(5,), dtype=int32)

Reshaped x:
tf.Tensor(
[[1]
 [2]
 [3]
 [4]
 [5]], shape=(5, 1), dtype=int32)

y:
tf.Tensor([1 2 3 4], shape=(4,), dtype=int32)
Result of Element-wise Multiplication:
tf.Tensor(
[[ 1  2  3  4]
 [ 2  4  6  8]
 [ 3  6  9 12]
 [ 4  8 12 16]
 [ 5 10 15 20]], shape=(5, 4), dtype=int32)

Let’s express the mathematical representation of the element-wise multiplication operation performed in the provided TensorFlow code:

Given the tensors \( x \) and \( y \):

(12.19)#\[\begin{equation} x = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \\ 5 \end{bmatrix} \end{equation}\]

(12.20)#\[\begin{equation} y = \begin{bmatrix} 1 & 2 & 3 & 4 \end{bmatrix} \end{equation}\]

The element-wise multiplication \( \text{result} \) is obtained by broadcasting \( y \) across the columns of \( x \):

(12.21)#\[\begin{equation} \text{result} = \begin{bmatrix} 1 \times 1 & 1 \times 2 & 1 \times 3 & 1 \times 4 \\ 2 \times 1 & 2 \times 2 & 2 \times 3 & 2 \times 4 \\ 3 \times 1 & 3 \times 2 & 3 \times 3 & 3 \times 4 \\ 4 \times 1 & 4 \times 2 & 4 \times 3 & 4 \times 4 \\ 5 \times 1 & 5 \times 2 & 5 \times 3 & 5 \times 4 \end{bmatrix} \end{equation}\]

Simplifying the multiplication results in the final element-wise product matrix:

(12.22)#\[\begin{equation} \text{result} = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 2 & 4 & 6 & 8 \\ 3 & 6 & 9 & 12 \\ 4 & 8 & 12 & 16 \\ 5 & 10 & 15 & 20 \end{bmatrix} \end{equation}\]

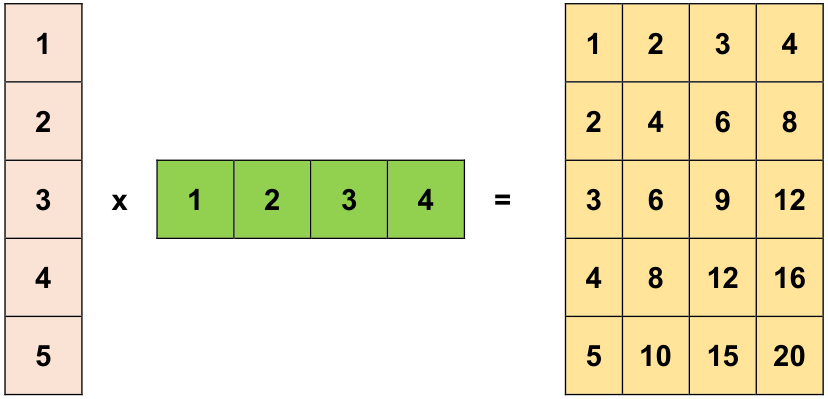
../_images/tf_broadcast.png — Fig. 12.9 A broadcasted addition occurs when a tensor with shape [5, 1] is combined with another tensor of shape [1, 4], resulting in a new tensor with shape [5, 4].#

Here is the same operation conducted without utilizing broadcasting:

# Import TensorFlow
import tensorflow as tf

# Define tensors for multiplication without broadcasting
x_stretch = tf.constant([[1, 1, 1, 1],
                         [2, 2, 2, 2],
                         [3, 3, 3, 3],
                         [4, 4, 4, 4],
                         [5, 5, 5, 5]])

y_stretch = tf.constant([[1, 2, 3, 4],
                         [1, 2, 3, 4],
                         [1, 2, 3, 4],
                         [1, 2, 3, 4],
                         [1, 2, 3, 4]])

# Perform element-wise multiplication without broadcasting
result = x_stretch * y_stretch

# Print the result
print_bold("Element-wise Multiplication Without Broadcasting:")
print(result)  # Operator overloading performs element-wise multiplication

Element-wise Multiplication Without Broadcasting:
tf.Tensor(
[[ 1  2  3  4]
 [ 2  4  6  8]
 [ 3  6  9 12]
 [ 4  8 12 16]
 [ 5 10 15 20]], shape=(5, 4), dtype=int32)

In the majority of cases, broadcasting proves to be efficient in terms of both time and space. This efficiency arises from the fact that the broadcast operation doesn’t physically create expanded tensors in memory [TensorFlow Developers, 2023].

To observe the visual representation of broadcasting, you can use the tf.broadcast_to function.

# Import TensorFlow
import tensorflow as tf

# Use tf.broadcast_to to demonstrate broadcasting
broadcasted_tensor = tf.broadcast_to(tf.constant([1, 2, 3]), [3, 3])

# Print the broadcasted tensor
print_bold("Broadcasted Tensor:")
print(broadcasted_tensor)

Broadcasted Tensor:
tf.Tensor(
[[1 2 3]
 [1 2 3]
 [1 2 3]], shape=(3, 3), dtype=int32)

Remark

Unlike certain mathematical operations, the broadcast_to function doesn’t implement memory-saving mechanisms. In this case, you are essentially creating the expanded tensor in memory [TensorFlow Developers, 2023].

12.3.9. Tensor Shapes and Indexing#

Tensors have shapes that describe how many elements they contain along each dimension. To work with tensors effectively, we need to understand some concepts related to their shapes [TensorFlow Developers, 2023]:

Shape: The shape of a tensor is a vector that shows the length (number of elements) of each dimension. For example, a tensor with shape [2, 3] has two dimensions, and each dimension has three elements.
Rank: The rank of a tensor is the number of dimensions it has. A scalar (a single number) has rank 0, a vector (a list of numbers) has rank 1, and a matrix (a table of numbers) has rank 2. The rank of a tensor is also the length of its shape vector.
Axis or Dimension: An axis or a dimension of a tensor is a specific direction or dimension that the tensor has. For example, a matrix has two axes: the first axis (axis 0) is the rows, and the second axis (axis 1) is the columns. We can use the axis index to access or modify a slice of a tensor along that axis.
Size: The size of a tensor is the total number of elements it contains. We can calculate the size of a tensor by multiplying the elements of its shape vector. For example, a tensor with shape [2, 3] has a size of 6.

These concepts help us understand the structure and dimensions of tensors, which are essential for working with TensorFlow [TensorFlow Developers, 2023].

12.3.9.1. Accessing Tensor Shapes with `tf.TensorShape` Objects#

Both tensors and tf.TensorShape objects have properties that allow us to access information about their shapes [TensorFlow Developers, 2023]:

ndim: This property returns the rank of the tensor, which is the number of dimensions it has. For example, a scalar has ndim of 0, a vector has ndim of 1, and a matrix has ndim of 2.
shape: This property gives a tuple of integers that represent the length of each dimension of the tensor. For example, a tensor with shape (2, 3) has two dimensions, and each dimension has three elements.
as_list(): This method converts the shape tuple to a Python list, which can be useful for manipulating or indexing the shape. For example, we can use as_list() to get the first element of the shape tuple, which is the size of the first dimension of the tensor.

Let’s see how we can use these properties to access the shapes of tensors [TensorFlow Developers, 2023]:

import tensorflow as tf

# Creating a Rank-4 Tensor
rank_4_tensor = tf.zeros([3, 2, 4, 5])

# Accessing shape information
shape_object = rank_4_tensor.shape
rank = rank_4_tensor.ndim
shape_list = rank_4_tensor.shape.as_list()

# Accessing shape and other information
print("Type of every element:" + 4*'\t', rank_4_tensor.dtype)
print("Number of axes:" + 5*'\t', rank_4_tensor.ndim)
print("Shape of tensor:"  + 4*'\t', rank_4_tensor.shape)
print("Elements along axis 0 of tensor:"  + 2*'\t', rank_4_tensor.shape[0])
print("Elements along the last axis of tensor:"  + 2*'\t', rank_4_tensor.shape[-1])
print("Total number of elements (3*2*4*5):"  + 2*'\t', tf.size(rank_4_tensor).numpy())

Type of every element:				 <dtype: 'float32'>
Number of axes:					 4
Shape of tensor:				 (3, 2, 4, 5)
Elements along axis 0 of tensor:		 3
Elements along the last axis of tensor:		 5
Total number of elements (3*2*4*5):		 120

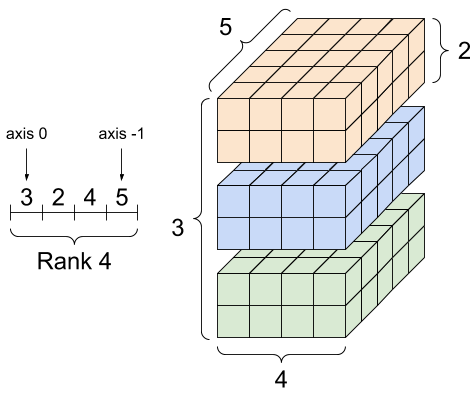
../_images/4d_tensor.png — Fig. 12.10 A rank-4 tensor, shape: [3, 2, 4, 5]. Image courtesy of TensorFlow documentation [TensorFlow Developers, 2023].#

12.3.10. Indexing Tensors#

12.3.10.1. Single-Axis Indexing#

TensorFlow employs standard Python indexing conventions, akin to indexing a list or a string in Python, and similar to NumPy indexing [TensorFlow Developers, 2023].

Here are the fundamental rules [TensorFlow Developers, 2023]:

Indexing begins at 0.
Negative indices count in reverse from the end.
Slices are defined using colons, :, in the format start:stop:step.

These indexing principles facilitate efficient access and manipulation of tensor elements, enabling you to work with tensors just like you would with arrays or lists in Python.

import tensorflow as tf

# Creating a tensor
tensor = tf.constant([0, 1, 1, 2, 3, 4, 8, 18, 21, 25, 101, 201])
print_bold("Original Tensor:")
print(tensor.numpy())  # Displaying the original tensor

# Indexing operations
print("First:", tensor[0].numpy())           # Access the first element (index 0)
print("Second:", tensor[1].numpy())          # Access the second element (index 1)
print("Last:", tensor[-1].numpy())           # Access the last element using negative index
print("Everything:", tensor[:].numpy())      # Access all elements (the entire tensor)
print("Before 4:", tensor[:4].numpy())       # Access elements up to but not including index 4
print("From 4 to the end:", tensor[4:].numpy())  # Access elements from index 4 to the end
print("From 2, before 7:", tensor[2:7].numpy())  # Access elements starting from index 2 up to but not including index 7
print("Every other item:", tensor[::2].numpy())  # Access every other element (step size of 2)
print("Reversed:", tensor[::-1].numpy())     # Access elements in reverse order

Original Tensor:
[  0   1   1   2   3   4   8  18  21  25 101 201]
First: 0
Second: 1
Last: 201
Everything: [  0   1   1   2   3   4   8  18  21  25 101 201]
Before 4: [0 1 1 2]
From 4 to the end: [  3   4   8  18  21  25 101 201]
From 2, before 7: [1 2 3 4 8]
Every other item: [  0   1   3   8  21 101]
Reversed: [201 101  25  21  18   8   4   3   2   1   1   0]

Explanation:

tensor[0].numpy() retrieves the first element of the tensor, which is 0.
tensor[1].numpy() retrieves the second element, which is 1.
tensor[-1].numpy() retrieves the last element, which is 201, using negative indexing.
tensor[:] accesses the entire tensor, resulting in [0, 1, 1, 2, 3, 4, 8, 18, 21, 25, 101, 201].
tensor[:4] gets elements up to but not including index 4, resulting in [0, 1, 1, 2].
tensor[4:] retrieves elements from index 4 to the end, giving [3, 4, 8, 18, 21, 25, 101, 201].
tensor[2:7] accesses elements starting from index 2 up to but not including index 7, yielding [1, 2, 3, 4, 8].
tensor[::2] retrieves every other element with a step size of 2, resulting in [0, 1, 3, 8, 21, 101].
tensor[::-1] accesses the elements in reverse order, giving [201, 101, 25, 21, 18, 8, 4, 3, 2, 1, 1, 0].

12.3.10.2. Multi-Axis Indexing#

For tensors with higher ranks (more dimensions), indexing involves passing multiple indices [TensorFlow Developers, 2023]. Crucially, the same rules as in the single-axis case apply to each axis independently. This means that you can apply the familiar indexing rules to each axis of the tensor, allowing for precise element selection within multi-dimensional structures [TensorFlow Developers, 2023].

# Creating a Rank-2 Tensor
rank_2_tensor = tf.constant([[1, 2, 3], [4, 5, 6]])

# Displaying the original tensor
print_bold("Original Tensor:")
print(rank_2_tensor.numpy())

# Indexing to retrieve a scalar value
print_bold("\nScalar Value at (1, 1):")
print(rank_2_tensor[1, 1].numpy())
# Indexing using a combination of integers and slices
print_bold("\nSecond row:")
print(rank_2_tensor[1, :].numpy())
print_bold("\nSecond column:")
print(rank_2_tensor[:, 1].numpy())
print_bold("\nLast row:")
print(rank_2_tensor[-1, :].numpy())
print_bold("\nFirst item in last column:")
print(rank_2_tensor[0, -1].numpy())
print_bold("\nSkip the first row:")
print(rank_2_tensor[1:, :].numpy())  # Outputs [[4 5 6]]

Original Tensor:
[[1 2 3]
 [4 5 6]]

Scalar Value at (1, 1):
5

Second row:
[4 5 6]

Second column:
[2 5]

Last row:
[4 5 6]

First item in last column:
3

Skip the first row:
[[4 5 6]]

# Creating a Rank-3 Tensor with Three Axes
# Here, we have a 3x2 grid of values, and
# there's an outer dimension encompassing them.
rank_3_tensor = tf.constant([[[11, 12, 13, 14], [15, 16, 17, 18]],
                             [[21, 22, 23, 24], [25, 26, 27, 28]],
                             [[31, 32, 33, 34], [35, 36, 37, 38]],
                             ])

# Displaying the Rank-3 Tensor
print_bold("Rank-3 Tensor with Three Axes:")
print(rank_3_tensor)

# Indexing along all axes to retrieve a 2D tensor
print_bold("\n2D Tensor along All Axes:")
print(rank_3_tensor[:, :, 3])

Rank-3 Tensor with Three Axes:
tf.Tensor(
[[[11 12 13 14]
  [15 16 17 18]]

 [[21 22 23 24]
  [25 26 27 28]]

 [[31 32 33 34]
  [35 36 37 38]]], shape=(3, 2, 4), dtype=int32)

2D Tensor along All Axes:
tf.Tensor(
[[14 18]
 [24 28]
 [34 38]], shape=(3, 2), dtype=int32)

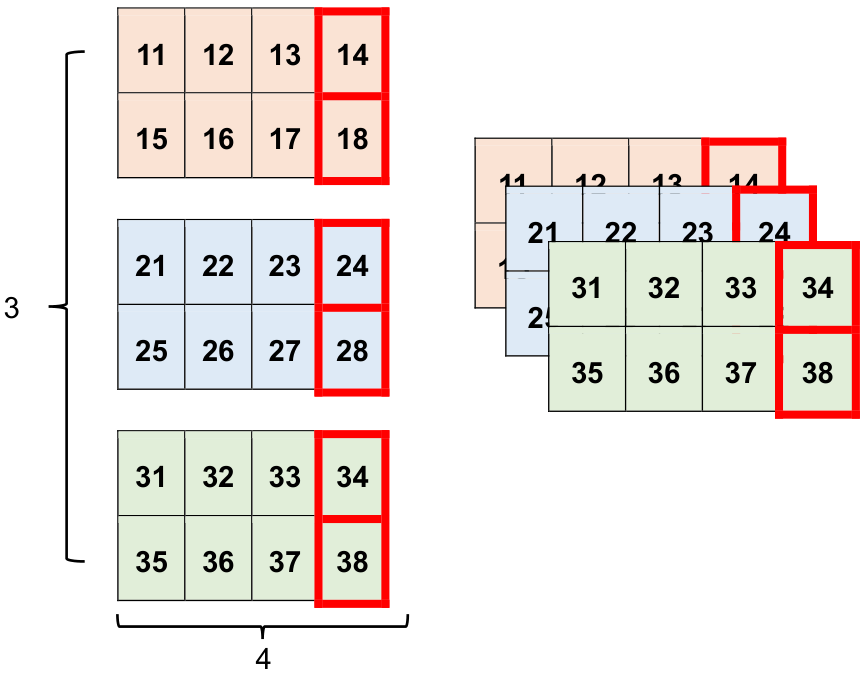
../_images/Multiaxis_indexing.png — Fig. 12.11 Selecting the final feature from all 2d slices.#

12.3.10.3. Reshaping Tensor Shapes#

The ability to reshape a tensor is incredibly valuable.

import tensorflow as tf

# Creating a tensor
x = tf.constant([[101], [102], [103], [104], [105]])

# Accessing shape information using shape property
shape_object = x.shape
print("Shape as TensorShape object:", shape_object)

# Converting TensorShape object to a Python list
shape_list = x.shape.as_list()
print("Shape as Python list:", shape_list)

Shape as TensorShape object: (5, 1)
Shape as Python list: [5, 1]

“Facilitating the transformation of tensor structures into novel configurations is a task of inherent importance. Notably, the tf.reshape operation stands out for its efficiency and resource efficiency, distinctively characterized by its avoidance of redundant data replication.”

import tensorflow as tf

# Creating a tensor
x = tf.constant([[101], [102], [103], [104], [105]])

# Reshaping the tensor to a new shape
reshaped = tf.reshape(x, [1, 5])

# Displaying original and reshaped shapes
print("Original Shape:", x.shape)
print("Reshaped Shape:", reshaped.shape)

Original Shape: (5, 1)
Reshaped Shape: (1, 5)

When reshaping a tensor in TensorFlow, the underlying data retains its original arrangement in memory. Instead of physically reorganizing the data, a new tensor with the desired shape is generated, while still referencing the same data in memory. TensorFlow follows a memory layout known as “row-major,” which means that the elements of a row are stored adjacently in memory. Consequently, incrementing the index on the rightmost side corresponds to traversing through memory in contiguous steps, effectively moving to the next element in the same row. This approach optimizes memory access patterns and aligns with the structure commonly used in C-style programming languages [TensorFlow Developers, 2023].

# Creating a Rank-3 Tensor with Three Axes
# Here, we have a 3x2 grid of values, and
# there's an outer dimension encompassing them.
rank_3_tensor = tf.constant([[[11, 12, 13, 14], [15, 16, 17, 18]],
                             [[21, 22, 23, 24], [25, 26, 27, 28]],
                             [[31, 32, 33, 34], [35, 36, 37, 38]],
                             ])

# Displaying the Rank-3 Tensor
print_bold("Rank-3 Tensor with Three Axes:")
print(rank_3_tensor)

Rank-3 Tensor with Three Axes:
tf.Tensor(
[[[11 12 13 14]
  [15 16 17 18]]

 [[21 22 23 24]
  [25 26 27 28]]

 [[31 32 33 34]
  [35 36 37 38]]], shape=(3, 2, 4), dtype=int32)

Flattening a tensor provides insight into the sequence in which its elements are organized within memory [TensorFlow Developers, 2023].

# Reshape the tensor using '-1'
# The '-1' indicates TensorFlow should determine the size along this axis automatically
flattened_tensor = tf.reshape(rank_3_tensor, [-1])

# Print the flattened tensor
print(flattened_tensor)

tf.Tensor([11 12 13 14 15 16 17 18 21 22 23 24 25 26 27 28 31 32 33 34 35 36 37 38], shape=(24,), dtype=int32)

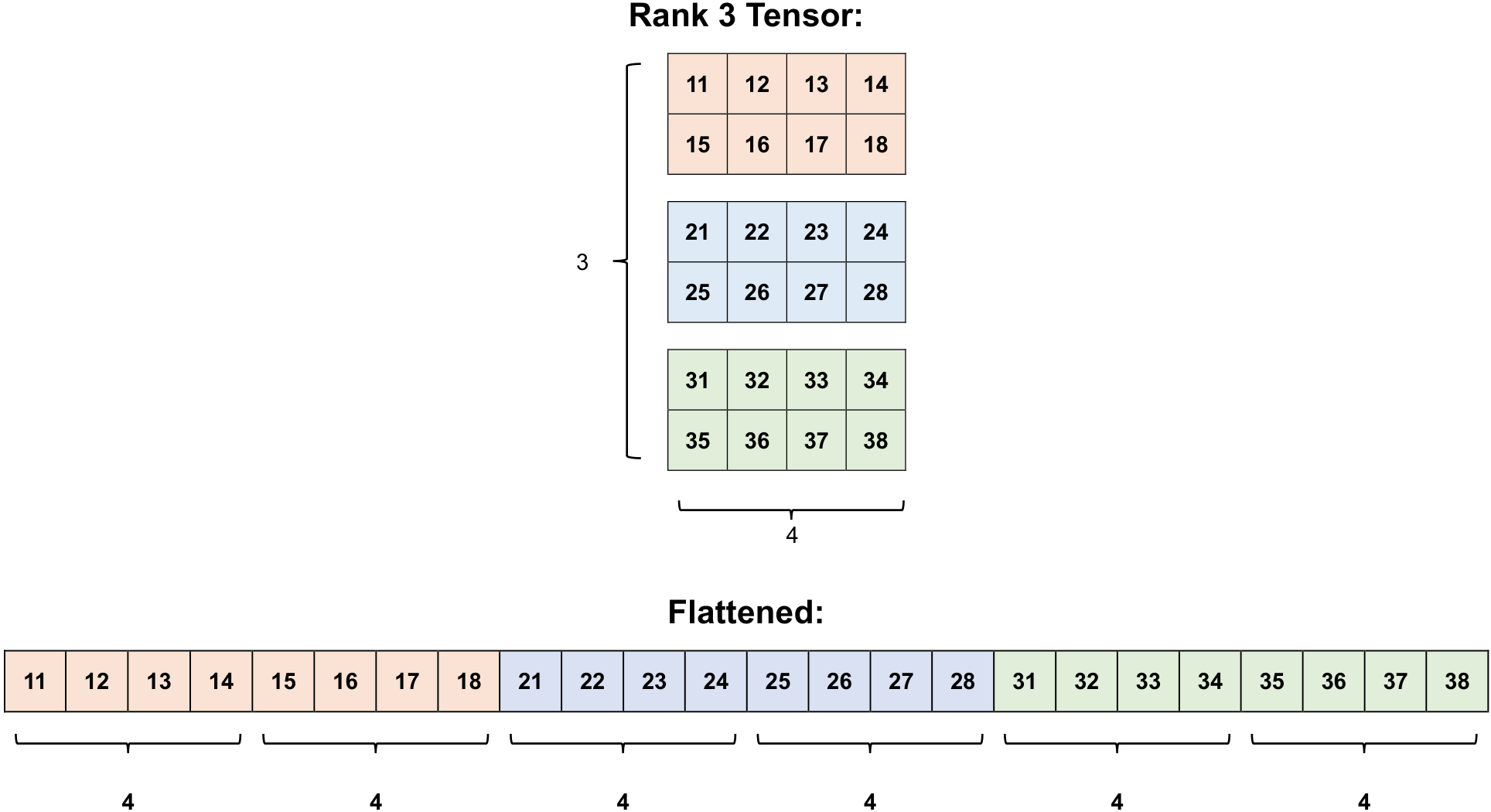
../_images/flattening_rank_3_tensor.png — Fig. 12.12 Flattening a rank 3 tensor.#

In this code, we’re using the -1 value in the shape argument of the tf.reshape function. This value essentially tells TensorFlow to calculate the size along that axis so that the total number of elements remains constant. The comments explain how the -1 value works and its purpose in the reshaping process.

Typically, the tf.reshape function is most useful when you need to merge or split neighboring axes, or when you want to add or remove dimensions with a size of 1 [TensorFlow Developers, 2023].

For the given 3x2x5 tensor, reshaping it into a (3x2)x5 format or into a 3x(2x5) format are both logical operations. This is because the reshaping maintains separate slices that do not overlap, allowing you to rearrange the data without mixing elements [TensorFlow Developers, 2023]:

Reshaping to (3x2)x5: This results in three rows of two-by-five matrices, effectively combining the inner dimensions. Each new row holds a set of elements that originally resided in different inner matrices.
Reshaping to 3x(2x5): This keeps the outermost dimension (3) intact while splitting the second dimension (2x5) into separate inner matrices. Each new column of the reshaped tensor contains elements from one of the original 2x5 matrices. Both reshaping approaches maintain the data integrity and relationships between elements [TensorFlow Developers, 2023].

print_bold('Reshape to (6, 4):')
print(tf.reshape(rank_3_tensor, [3*2, 4]))
print_bold('\nReshape to (3, 8):')
print(tf.reshape(rank_3_tensor, [3, -1]))

Reshape to (6, 4):
tf.Tensor(
[[11 12 13 14]
 [15 16 17 18]
 [21 22 23 24]
 [25 26 27 28]
 [31 32 33 34]
 [35 36 37 38]], shape=(6, 4), dtype=int32)

Reshape to (3, 8):
tf.Tensor(
[[11 12 13 14 15 16 17 18]
 [21 22 23 24 25 26 27 28]
 [31 32 33 34 35 36 37 38]], shape=(3, 8), dtype=int32)

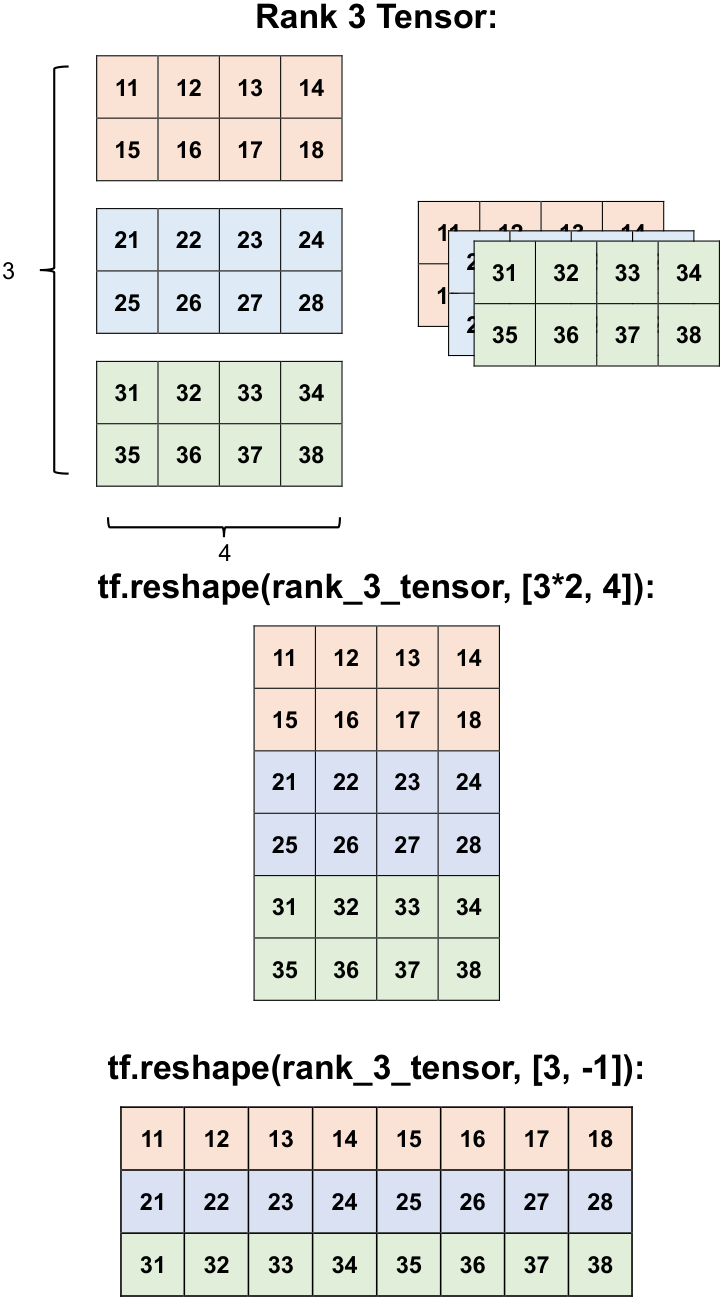
../_images/tf_reshape.png — Fig. 12.13 Visualizing reshaping `rank_3_tensor` tensor.#

Reshaping a tensor can be successfully performed for any new shape that maintains the same total count of elements. However, it’s important to note that reshaping won’t yield meaningful results if the arrangement of axes isn’t honored [TensorFlow Developers, 2023].

If you intend to rearrange the order of axes, using tf.reshape won’t suffice. Instead, for swapping or permuting axes, the appropriate function to use is tf.transpose. Reshaping merely alters the dimensions while preserving the sequence of elements, ensuring that you maintain the correct data relationships. Conversely, when you need to modify the order of the dimensions, such as swapping axes, tf.transpose is the suitable choice to achieve that specific transformation [TensorFlow Developers, 2023].

import tensorflow as tf

# Define a Rank-3 tensor
rank_3_tensor = tf.constant([
    [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]],
    [[10, 11, 12, 13, 14], [15, 16, 17, 18, 19]],
    [[20, 21, 22, 23, 24], [25, 26, 27, 28, 29]],
])

# Examples of incorrect reshaping

# You can't reorder axes with reshape.
print("Cannot reorder axes with reshape:")
print(tf.reshape(rank_3_tensor, [2, 3, 5]), "\n")

# Incorrect dimensions specified.
print("Incorrect dimensions specified:")
print(tf.reshape(rank_3_tensor, [5, 6]), "\n")

# Incompatible reshape dimensions.
try:
    tf.reshape(rank_3_tensor, [7, -1])
except Exception as e:
    print("Incompatible reshape dimensions:")
    print(f"{type(e).__name__}: {e}")

Cannot reorder axes with reshape:
tf.Tensor(
[[[ 0  1  2  3  4]
  [ 5  6  7  8  9]
  [10 11 12 13 14]]

 [[15 16 17 18 19]
  [20 21 22 23 24]
  [25 26 27 28 29]]], shape=(2, 3, 5), dtype=int32) 

Incorrect dimensions specified:
tf.Tensor(
[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]
 [12 13 14 15 16 17]
 [18 19 20 21 22 23]
 [24 25 26 27 28 29]], shape=(5, 6), dtype=int32) 

Incompatible reshape dimensions:
InvalidArgumentError: {{function_node __wrapped__Reshape_device_/job:localhost/replica:0/task:0/device:CPU:0}} Input to reshape is a tensor with 30 values, but the requested shape requires a multiple of 7 [Op:Reshape]

[TensorFlow Developers, 2023]

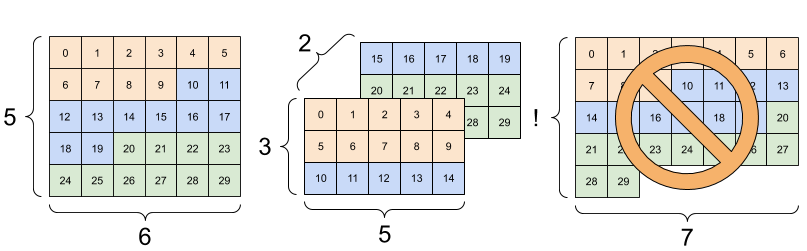
../_images/tf_reshape_bad.png — Fig. 12.14 Visualizing reshaping `rank_3_tensor` tensor (incorrect reshaping). Image courtesy of TensorFlow documentation [TensorFlow Developers, 2023].#

12.3.11. Ragged Tensors#

A tensor that possesses varying numbers of elements along a specific axis is referred to as “ragged.” To handle such data, the tf.ragged.RaggedTensor class comes into play [TensorFlow Developers, 2023].

For instance, the following data structure cannot be accurately represented using a standard tensor [TensorFlow Developers, 2023]:

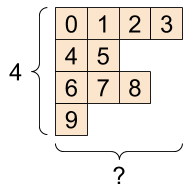
../_images/ragged.png — Fig. 12.15 A `tf.RaggedTensor` with a shape of [4, None] aptly addresses this scenario. Image courtesy of TensorFlow documentation [TensorFlow Developers, 2023].#

import tensorflow as tf

# Define a ragged list
ragged_list = [
    [0, 1, 2, 3],
    [4, 5],
    [6, 7, 8],
    [9]]

# Attempt to create a tensor from the ragged list
try:
    tensor = tf.constant(ragged_list)
except Exception as e:
    print("Error:", f"{type(e).__name__}: {e}")

Error: ValueError: Can't convert non-rectangular Python sequence to Tensor.

Instead create a tf.RaggedTensor using tf.ragged.constant:

import tensorflow as tf

# Define a ragged list
ragged_list = [
    [0, 1, 2, 3],
    [4, 5],
    [6, 7, 8],
    [9]]

# Create a tf.RaggedTensor using tf.ragged.constant
ragged_tensor = tf.ragged.constant(ragged_list)

# Print the ragged tensor
print("Ragged Tensor:")
print(ragged_tensor)

Ragged Tensor:
<tf.RaggedTensor [[0, 1, 2, 3], [4, 5], [6, 7, 8], [9]]>

The shape of a tf.RaggedTensor will contain some axes with unknown lengths:

print(ragged_tensor.shape)

(4, None)

You can learn more about ragged tensors here.