11.2. Principal Components Analysis (PCA)

Principal Components Analysis (PCA) is a widely used statistical technique that plays a crucial role in reducing the dimensionality of high-dimensional data while retaining its inherent variability. This is accomplished by transforming the original variables into a new set of uncorrelated variables called principal components. These principal components are linear combinations of the original variables, and they are ordered in such a way that the first component explains the maximum variance, the second component explains the second highest variance, and so on.

11.2.1. Mathematical Formulation

PCA is a powerful tool when dealing with a large set of interconnected variables, enabling the compression of this set into a smaller group of representative variables that collectively capture the major part of the initial set’s variability. This is particularly valuable for tasks such as data visualization and exploratory analysis [James et al., 2023].

Consider a scenario where we possess data on n observations, each with measurements across a collection of p features denoted as \(X_1\), \(X_2\), \(\ldots\), \(X_p\).

1. Given a dataset represented by an \(n \times p\) matrix X, the loading vector of the first principal component is determined by solving the subsequent optimization problem:

   (11.1)\[\begin{align} \max_{\phi_{11}, \ldots, \phi_{p1}} \left\{ \frac{1}{n} \sum_{i=1}^{n} \left( \sum_{j=1}^{p} \phi_{j1} x_{ij} \right)^2 \right\}, \quad \text{subject to} \sum_{j=1}^{p} \phi_{j1}^2. \end{align}\]

   Introducing an intermediate variable \(z_{ij} = \sum_{j=1}^{p} \phi_{j1} x_{ij}\) allows us to reformulate the problem:

   (11.2)\[\begin{align} \max_{\phi_{11}, \ldots, \phi_{p1}} \left\{ \frac{1}{n} \sum_{i=1}^{n} z_{ij}^2 \right\}, \quad \text{subject to} \sum_{j=1}^{p} \phi_{j1}^2. \end{align}\]

   Importantly, \(\frac{1}{n}\sum_{i=1}^{n} z_{ij}^2 = 0\) due to \(\frac{1}{n}\sum_{i=1}^{n} x_{ij} = 0\). Furthermore, the terms \(z_{ij}\) are commonly known as the scores of the first principal component.

2. The second principal component can be understood as the linear combination of \(X_1\), \(X_2\), \(\ldots\), \(X_p\) that possesses the highest variance among all linear combinations that are uncorrelated with the first principal component, denoted as \(Z_1\). The scores of the second principal component, represented as \(z_{12}\), \(z_{22}\), \(\ldots\), \(z_{n2}\), are given by the formula:

   \[z_{i2} = \sum_{j=1}^{p} \phi_{j2} x_{ij}\]

   In this context, \(\phi_{2} = \left[ \phi_{12}, \phi_{22}, \ldots, \phi_{p2} \right]\) indicates the loading vector associated with the second principal component. Essentially, this vector captures the weightings assigned to each feature when constructing the second principal component.

11.2.2. The Essence of Principal Components Analysis (PCA)

Objective: PCA aims to find a set of orthogonal axes (principal components) in the high-dimensional space that captures the most significant variance in the data [Jolliffe, 2013].

Steps:

1. Data Standardization: Before performing PCA, it’s common to standardize the data to have zero mean and unit variance. This is crucial as it ensures that variables with larger scales don’t disproportionately influence the analysis [Jolliffe, 2013].

2. Covariance Matrix: Calculate the covariance matrix of the standardized data. The covariance matrix represents the relationships between the variables [Jolliffe, 2013].

3. Eigenvalue Decomposition: Compute the eigenvalues and eigenvectors of the covariance matrix. The eigenvectors are the directions of the principal components, and the corresponding eigenvalues indicate the amount of variance explained by each component [Jolliffe, 2013].

4. Principal Component Scores: Project the original data onto the principal component axes to obtain the principal component scores. These scores represent the data in the new coordinate system defined by the principal components [Jolliffe, 2013].

Applications:

1. Dimensionality Reduction: PCA is used to reduce the number of dimensions while retaining the most important information. This is particularly helpful when dealing with high-dimensional data that can be difficult to visualize or analyze [Jolliffe, 2013].

2. Data Visualization: By plotting the data using the first two principal components as axes, it’s possible to visualize the inherent structure of the data in a lower-dimensional space [Jolliffe, 2013].

3. Noise Reduction: PCA can help reduce noise in the data by focusing on the components that explain the most variance and potentially ignoring noise-dominated components [Jolliffe, 2013].

4. Feature Selection: In some cases, PCA can be used as a form of feature selection, as it provides insights into which original features contribute most to the principal components [Jolliffe, 2013].

Limitations:

1. Loss of Interpretability: While PCA is powerful for dimensionality reduction, the resulting principal components might not have a direct interpretation in terms of the original features [Jolliffe, 2013].

2. Linearity Assumption: PCA assumes that the underlying relationships in the data are linear. If the data exhibits nonlinear relationships, PCA might not be the most suitable technique [Jolliffe, 2013].

3. Information Loss: Although PCA retains most of the variance, there is some amount of information loss when reducing dimensions [Jolliffe, 2013].

PCA algorithm

The PC (Principal Component) algorithm is a technique used for dimensionality reduction and feature extraction. It aims to find a set of orthogonal axes, called principal components, along which the data varies the most. These principal components are linear combinations of the original features. Below, I’ll outline the mathematical steps of the PC algorithm [Phillips, 2023]:

Step 1: Data Preprocessing

• Collect and preprocess the dataset if needed. Ensure that the data is centered (i.e., subtract the mean from each feature) to have a mean of zero.

Step 2: Calculate the Covariance Matrix

• Compute the covariance matrix (\( \Sigma \)) of the preprocessed data. The covariance between two features \( x_i \) and \( x_j \) is given by:

  (11.3)\[\begin{equation} \text{Cov}(x_i, x_j) = \frac{1}{n-1} \sum_{k=1}^{n} (x_i^{(k)} - \bar{x}_i)(x_j^{(k)} - \bar{x}_j) \end{equation}\]

  Where:

  • \( n \) is the number of data points.

  • \( x_i^{(k)} \) and \( x_j^{(k)} \) are the values of features \( x_i \) and \( x_j \) for data point \( k \).

  • \( \bar{x}_i \) and \( \bar{x}_j \) are the means of features \( x_i \) and \( x_j \) across all data points.

• The covariance matrix \( \Sigma \) is a symmetric matrix where each element \( \Sigma_{ij} \) represents the covariance between features \( x_i \) and \( x_j \).

Step 3: Eigendecomposition

• Perform an eigendecomposition on the covariance matrix \( \Sigma \) to find its eigenvalues (\( \lambda_1, \lambda_2, \ldots, \lambda_p \)) and corresponding eigenvectors (\( \mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_p \)), where \( p \) is the number of features.

Step 4: Sort Eigenvalues and Eigenvectors

• Sort the eigenvalues in descending order, and arrange the corresponding eigenvectors accordingly.

Step 5: Select Principal Components

• Choose the top \( k \) eigenvectors corresponding to the \( k \) largest eigenvalues to form a matrix \( \mathbf{V}_k \). These are the principal components that capture the most variance in the data.

Step 6: Projection

• Project the original data onto the subspace spanned by the selected \( k \) principal components to obtain the reduced-dimensional representation of the data. The projection of a data point \( \mathbf{x} \) onto the subspace is given by:

  (11.4)\[\begin{equation} \mathbf{X}_{\text{new}} = \mathbf{X} \cdot \mathbf{V}_k \end{equation}\]

  Where:

  • \( \mathbf{X}_{\text{new}} \) is the reduced-dimensional data.

  • \( \mathbf{X} \) is the original centered data.

  • \( \mathbf{V}_k \) is the matrix of the top \( k \) principal components.

The result is a transformed dataset that retains most of the variance while reducing the dimensionality.

The PC algorithm is a fundamental technique in dimensionality reduction and feature extraction, often used as a precursor to other machine learning tasks to reduce computational complexity and noise in the data.

Calculation of Covarinace

The covariance between two variables measures the extent to which they vary together. Mathematically, the covariance between two variables \(X\) and \(Y\) is calculated as [Witte and Witte, 2017]:

(11.5)\[\begin{equation} \text{Cov}(X, Y) = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) \end{equation}\]

Where:

• \( n \) is the number of data points.

• \( x_i \) and \( y_i \) are the values of variables \(X\) and \(Y\) for the \(i\)th data point.

• \( \bar{x} \) and \( \bar{y} \) are the means of variables \(X\) and \(Y\) across all data points.

Covariance can also be calculated using matrix operations. If you have a dataset with multiple variables, you can calculate the covariance matrix \( \Sigma \) as follows:

(11.6)\[\begin{equation} \Sigma = \frac{1}{n-1} \cdot (\mathbf{X} - \mathbf{\bar{x}})^\top \cdot (\mathbf{X} - \mathbf{\bar{x}}) \end{equation}\]

Where:

• \( \mathbf{X} \) is an \( n \times p \) matrix representing the dataset, where \( n \) is the number of data points and \( p \) is the number of variables.

• \( \mathbf{\bar{x}} \) is a \( 1 \times p \) vector containing the means of each variable.

The resulting covariance matrix \( \Sigma \) is a \( p \times p \) symmetric matrix. The element \( \Sigma_{ij} \) represents the covariance between variables \(X_i\) and \(X_j\).

In Python, you can calculate the covariance matrix using the np.cov function from the NumPy library. Here’s an example:

import numpy as np

# Define a dataset
data = np.array([[x1, y1], [x2, y2], ...])

# Calculate the covariance matrix
cov_matrix = np.cov(data.T)

The diagonal elements of the covariance matrix represent the variances of individual variables, while the off-diagonal elements represent the covariances between pairs of variables.

Example: Let’s consider a small dataset with two variables (\(X_1\) and \(X_2\)) and three observations:

Step 1: Define the Dataset The new original dataset is given by the matrix \(A\):

(11.7)\[\begin{equation} A = \begin{bmatrix} 11 & 22 \\ 13 & 24 \\ 15 & 26 \\ \end{bmatrix} \end{equation}\]

This matrix represents a dataset with three data points, where each row corresponds to a data point and each column corresponds to a feature. In this case, you have three data points and two features.

Explanation: This step defines the input data for PCA. The matrix \(A\) contains the values of the two features (\(X_1\) and \(X_2\)) for each data point. For example, the first data point has \(X_1 = 11\) and \(X_2 = 22\).

Step 2: Calculate the Mean of Each Column Calculate the mean of each feature (column) to obtain the column-wise means:

(11.8)\[\begin{equation} M = \begin{bmatrix} \dfrac{11+13+15}{3} \\ \dfrac{22+24+26}{3} \\ \end{bmatrix} = \begin{bmatrix} 13 \\ 24 \\ \end{bmatrix} \end{equation}\]

Here, \(M\) represents the mean vector, where each element \( M_i \) corresponds to the mean of feature \( i \).

Explanation: This step calculates the average value of each feature across all data points. The mean vector \(M\) summarizes the central tendency of the data for each feature. For example, the mean of feature \(X_1\) is \(13\), which is the average of \(11\), \(13\), and \(15\).

Step 3: Center Columns by Subtracting Column Means Center the data by subtracting the mean vector \( M \) from each data point in matrix \( A \), resulting in the centered matrix \( C \):

(11.9)\[\begin{equation} C = A - M = \begin{bmatrix} 11-13 & 22-24 \\ 13-13 & 24-24 \\ 15-13 & 26-24 \\ \end{bmatrix} = \begin{bmatrix} -2 & -2 \\ 0 & 0 \\ 2 & 2 \\ \end{bmatrix} \end{equation}\]

Explanation: This step centers the data by removing the mean from each feature. The centered matrix \(C\) contains the deviations of the original values from the mean. This ensures that the data has zero mean and reduces the effect of scaling differences among features. For example, the first data point has a deviation of \(-2\) from the mean of feature \(X_1\).

Step 4: Calculate Covariance Matrix of Centered Matrix Consider that \(X\) represents a 3 by 2 matrix, implying that the sample size, denoted as \(n\), equals 3. We can now compute the covariance matrix \(V\) for the centered matrix \(C\) by performing the matrix multiplication of the transpose of \(C\) by \(C\):

(11.10)\[\begin{equation} \Sigma = \frac{1}{n-1}C^T C = \frac{1}{3-1} \begin{bmatrix} -2 & 0 & 2 \\ -2 & 0 & 2 \\ \end{bmatrix} \begin{bmatrix} -2 & -2 \\ 0 & 0 \\ 2 & 2 \\ \end{bmatrix} = \begin{bmatrix} 4 & 4 \\ 4 & 4 \\ \end{bmatrix} \end{equation}\]

The covariance matrix \( V \) captures the relationships between the features and their variations.

Explanation: This step calculates the covariance matrix of the centered data. The covariance matrix measures the relationship between each pair of features in the data. Each element is the covariance between two features, which indicates how they vary together. A high positive covariance means that the features tend to increase or decrease together, while a high negative covariance means that they tend to move in opposite directions. A zero covariance means that the features are independent of each other. For example, the covariance between feature \(X_1\) and feature \(X_2\) is \(4\), which means that they have a strong positive relationship.

Step 5: Eigendecomposition of Covariance Matrix Perform the eigendecomposition of the covariance matrix \(\Sigma\) to find eigenvalues and eigenvectors. Eigenvalues (\( \lambda \)) represent the importance of each eigenvector, and eigenvectors (\( V \)) define the directions of the new feature space:

(11.11)\[\begin{equation} \lambda = \begin{bmatrix} 8 \\ 0 \\ \end{bmatrix} \end{equation}\]

(11.12)\[\begin{equation} V = \begin{bmatrix} \dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \\ \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{2}}{2} \\ \end{bmatrix} \end{equation}\]

Explanation: This step performs the eigendecomposition of the covariance matrix to find its eigenvalues and eigenvectors. The eigenvalues represent the amount of variance explained by each eigenvector, which are the directions of the principal components. The principal components are the new features that capture the most significant variations in the data. They are ordered by decreasing eigenvalues, meaning that the first principal component explains the most variance, the second principal component explains the second most variance, and so on. For example, the first eigenvalue is \(8\), which means that the first principal component accounts for all the variance in the data, while the second eigenvalue is \(0\), which means that the second principal component contributes nothing to the variance.

Step 6: Project Data Project the centered data matrix \( C \) onto the eigenvectors to obtain the transformed data \( P \). The transformation is performed by calculating the dot product between the transposed eigenvectors and the transposed centered data matrix:

\[\begin{align*} P^T = V^T C^T & = \begin{bmatrix} \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{2}}{2} \\ -\dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{2}}{2} \\ \end{bmatrix} \begin{bmatrix} -2 & 0 & 2 \\ -2 & 0 & 2 \\ \end{bmatrix} \\ & = \begin{bmatrix} -2\sqrt{2} & 0 & 2\sqrt{2} \\ 0 & 0 & 0 \\ \end{bmatrix} \end{align*}\]

Transformed Data (Projected onto Principal Components):

\[\begin{align*} P = \begin{bmatrix} -2\sqrt{2} & 0 \\ 0 & 0 \\ 2\sqrt{2} & 0 \\ \end{bmatrix} \end{align*}\]

The resulting matrix \( P\) represents the data projected onto the new feature space defined by the eigenvectors. This transformation effectively reduces the dimensionality while retaining the maximum variance in the data.

Explanation: This step projects the centered data matrix onto the eigenvectors to obtain the transformed data. The transformed data is in a new coordinate system defined by the principal components, where the axes are aligned with the directions of maximum variance in the data. The values in the transformed data represent the projections of the original data points onto the principal components, which indicate how much each principal component contributes to the data point’s transformation. For example, the first data point has a projection of \(-2\sqrt{2}\) along the first principal component and \(0\) along the second principal component, which means that it is located far away from the origin along the diagonal line defined by the first principal component.

Note

To find the eigenvalues and eigenvectors, we can use the following steps:

• First, we need to find the characteristic polynomial of the matrix, which is given by the determinant of the matrix minus a scalar variable lambda. For the matrix \(A = \begin{bmatrix} 4 & 4 \\ 4 & 4 \\ \end{bmatrix}\), the characteristic polynomial is:

\[\begin{split} \det(\lambda I - A) = \begin{vmatrix}4 - \lambda & 4 \\4 & 4 - \lambda\end{vmatrix}= (4 - \lambda)^2 - 16 = \lambda^2 - 8\lambda \end{split}\]

• Next, we need to find the roots of the characteristic polynomial, which are the eigenvalues of the matrix. We can use the quadratic formula to solve for lambda:

\[ \lambda = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{8 \pm \sqrt{64 - 0}}{2} = \frac{8 \pm 8}{2} = 0, 8 \]

• The eigenvalues of the matrix are 0 and 8.

• To find the eigenvectors of the matrix, we need to plug in each eigenvalue into the equation \((A - \lambda I)X = 0\), and solve for the vector.

  • For the eigenvalue 0, we have:

  \[\begin{split} \begin{bmatrix} 4 - 0 & 4 \\ 4 & 4 - 0 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \end{split}\]

  • This gives us the equation \(4x + 4y = 0\), which implies that \(x = -y\). Therefore, any vector of the form \([-y, y]\) is an eigenvector for the eigenvalue \(0\). For example, \([-1, 1]\) is an eigenvector for \(0\).

  • For the eigenvalue 8, we have:

  \[\begin{split} \begin{bmatrix} 4 - 8 & 4 \\ 4 & 4 - 8 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \end{split}\]

  • This gives us the equation \(-4x + 4y = 0\), which implies that \(x = y\). Therefore, any vector of the form \([y, y]\) is an eigenvector for the eigenvalue 8. For example, \([1, 1]\) is an eigenvector for 8.

  • The eigenvectors of the matrix are \([-y, y]\) for 0 and \([y, y]\) for 8.

To form an eigenvector matrix V, we need to choose one eigenvector for each eigenvalue and arrange them as columns of the matrix. For example, we can choose \([-1, 1]\) for 0 and \([1, 1]\) for 8. Then, the eigenvector matrix \(V\) is:

\[\begin{split} V = \begin{bmatrix} -1 & 1 \\ 1 & 1 \end{bmatrix} \end{split}\]

To normalize the eigenvector matrix V, we need to divide each column by its norm, which is the square root of the sum of the squares of its elements. For example, the norm of [-1, 1] is \(\sqrt{(-1)^2 + (1)^2} = \sqrt{2}\). Then, the normalized eigenvector matrix V is:

\[\begin{split} V = \dfrac{1}{\sqrt{2}} \begin{bmatrix} -1 & 1 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} -\dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} \\ \dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} \end{bmatrix} \end{split}\]

Note

Principal Component Analysis (PCA) was conducted on a dataset containing three data points and two features. PCA is a data transformation technique designed to create a new feature space that maximizes data variance while minimizing redundancy. This new feature space is characterized by the eigenvectors of the dataset’s covariance matrix, often referred to as principal components. The eigenvalues of the covariance matrix provide insight into the significance of each principal component concerning data variance.

The above calculations can be summarized as follows:

• The covariance matrix of the original dataset, denoted as \(\Sigma\), is given by:

  (11.13)\[\begin{equation} \Sigma = \begin{bmatrix} 4 & 4 \\ 4 & 4 \\ \end{bmatrix} \end{equation}\]

  This indicates a perfect correlation between the two features and equal variances. Consequently, the data exhibits substantial redundancy, suggesting the potential for dimensionality reduction without significant information loss.

• The eigenvalues of the covariance matrix, represented as \(\lambda\), are as follows:

  (11.14)\[\begin{equation} \lambda = \begin{bmatrix} 8 \\ 0 \\ \end{bmatrix} \end{equation}\]

  These eigenvalues signify that the first principal component explains all the data variance, while the second principal component contributes none. Consequently, projecting the data onto a one-dimensional space defined by the first principal component preserves all essential information.

• The eigenvectors of the covariance matrix, denoted as \(V\), are given by:

  (11.15)\[\begin{equation} V = \begin{bmatrix} \dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \\ \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{2}}{2} \\ \end{bmatrix} \end{equation}\]

  These eigenvectors specify that the first principal component is a 45-degree diagonal line, while the second principal component is perpendicular to it. These directions define the new feature space for data transformation.

• The data projected onto the principal components, designated as \(P\), is represented as:

  (11.16)\[\begin{equation} P = \begin{bmatrix} -2\sqrt{2} & 0 \\ 0 & 0 \\ 2\sqrt{2} & 0 \\ \end{bmatrix} \end{equation}\]

  This projection effectively reduces the data from two dimensions to one dimension by utilizing only the first column of \(P\). It is evident that the projected data points are evenly spaced along the first principal component and possess zero values along the second principal component.

Remark

The matrix \( P \) represents the transformed data obtained after applying Principal Component Analysis (PCA) to the original dataset. Each row of \( P \) corresponds to a data point in the original dataset, and each column corresponds to a principal component.

In the context of PCA, the principal components are orthogonal directions in the original feature space that capture the most significant variations in the data. The first principal component (column 1 of \( P \)) captures the maximum variance, the second principal component (column 2 of \( P \)) captures the second highest variance, and so on.

The values in the matrix \( P \) represent the projections of the original data points onto these principal components. These projections are in a new coordinate system defined by the principal components, where the axes are aligned with the directions of maximum variance in the data.

Interpreting the matrix \( P \):

• Each row in \( P \) represents a transformed data point.

• The values in each row represent how the original features have been projected onto the principal components.

• The magnitude of each value indicates the contribution of the corresponding principal component to the transformation of that data point.

For example, if the first column of \( P \) has relatively large values for a particular data point, it means that this data point has a significant projection along the direction of the first principal component, capturing a large amount of the overall variance in the data. Similarly, the second column of \( P \) captures the second principal component’s contribution to each data point’s transformation.

The matrix \( P \) provides a reduced-dimensional representation of the original data in terms of the principal components. It captures the essential information while discarding less significant variations in the data, which is the primary goal of PCA.

Example: We can employ the numpy library in Python to perform Principal Component Analysis (PCA), as illustrated in the preceding instance.

import numpy as np
from pprint import pprint

def print_bold(txt):
    _left = "\033[1;34m"
    _right = "\033[0m"
    print(_left + txt + _right)

# Define a matrix
A = np.array([[11, 22], [13, 24], [15, 26]])

# Step 1: Print the original dataset
print_bold("Step 1: Original Dataset:")
print(A)

# Step 2: Calculate the mean of each column
M = np.mean(A, axis=0)
print_bold("\nStep 2: Mean of Each Column:")
print(M)

# Step 3: Center columns by subtracting column means
C = A - M
print_bold("\nStep 3: Centered Columns:")
print(C)

# Step 4: Calculate covariance matrix of centered matrix
Sigma = np.cov(C.T)
print_bold("\nStep 4: Covariance Matrix of Centered Matrix:")
print(Sigma)

# Step 5: Eigendecomposition of covariance matrix
lambda_, V = np.linalg.eig(Sigma)
print_bold("\nStep 5: Eigendecomposition of Covariance Matrix")
print_bold(f"Eigenvalues:")
print(lambda_)
print_bold(f"Eigenvectors:")
print(V)

# Step 6: Project data
P = np.dot(V.T, C.T)
print_bold("\nStep 6: Projected Data:")
pprint(P.T)

Step 1: Original Dataset:
[[11 22]
 [13 24]
 [15 26]]

Step 2: Mean of Each Column:
[13. 24.]

Step 3: Centered Columns:
[[-2. -2.]
 [ 0.  0.]
 [ 2.  2.]]

Step 4: Covariance Matrix of Centered Matrix:
[[4. 4.]
 [4. 4.]]

Step 5: Eigendecomposition of Covariance Matrix
Eigenvalues:
[8. 0.]
Eigenvectors:
[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

Step 6: Projected Data:
array([[-2.82842712,  0.        ],
       [ 0.        ,  0.        ],
       [ 2.82842712,  0.        ]])

Here is what each step means:

• Step 1: Original Dataset: This is the matrix that represents your data before applying PCA. Each row corresponds to a data point, and each column corresponds to a feature. In this case, you have three data points and two features.

• Step 2: Mean of Each Column: This is the vector that contains the average value of each feature across all data points. This is used to center the data by subtracting the mean from each feature.

• Step 3: Centered Columns: This is the matrix that represents your data after centering. Each element is the difference between the original value and the mean of the corresponding feature. This ensures that the data has zero mean and reduces the effect of scaling differences among features.

• Step 4: Covariance Matrix of Centered Matrix: This is the matrix that measures the relationship between each pair of features in the centered data. Each element is the covariance between two features, which indicates how they vary together. A high positive covariance means that the features tend to increase or decrease together, while a high negative covariance means that they tend to move in opposite directions. A zero covariance means that the features are independent of each other.

• Step 5: Eigendecomposition of Covariance Matrix: This is the process of finding the eigenvalues and eigenvectors of the covariance matrix. The eigenvalues represent the amount of variance explained by each eigenvector, which are the directions of the principal components. The principal components are the new features that capture the most significant variations in the data. They are ordered by decreasing eigenvalues, meaning that the first principal component explains the most variance, the second principal component explains the second most variance, and so on.

• Step 6: Projected Data: This is the matrix that represents your data after transforming it to the new feature space defined by the principal components. Each row corresponds to a data point, and each column corresponds to a principal component. The values are the projections of the original data points onto the principal components, which indicate how much each principal component contributes to the data point’s transformation.

Example: We can utilize the scikit-learn library in Python to conduct Principal Component Analysis (PCA), as shown in the previous example.

from sklearn.decomposition import PCA

# Define a matrix
A = np.array([[11, 22], [13, 24], [15, 26]])

# Step 1: Print the original dataset
print_bold("Step 1: Original Dataset:")
pprint(A)

# Step 2: Create the PCA instance with desired number of components
pca = PCA()

# Step 3: Fit the PCA model on the data
pca.fit(A)
print_bold("Step 3: Fit PCA Model on Data")

# Step 4: Access principal components (eigenvectors) and explained variance
print_bold("\nStep 4: Access Principal Components and Explained Variance")
print_bold("Principal Components (Eigenvectors):")
pprint(pca.components_)
print_bold("Explained Variance for Each Principal Component:")
pprint(pca.explained_variance_)

# Step 5: Eigendecomposition of Covariance Matrix
print_bold("\nStep 5: Eigendecomposition of Covariance Matrix")
print_bold("Eigenvalues:")
pprint(pca.explained_variance_)
print_bold("Eigenvectors:")
pprint(pca.components_)

# Step 6: Transform data using PCA
P = pca.transform(A)
print_bold("\nStep 6: Transform Data using PCA (Projection)")
print_bold("Transformed Data (Projected onto Principal Components):")
pprint(np.round(P, 6))

Step 1: Original Dataset:
array([[11, 22],
       [13, 24],
       [15, 26]])
Step 3: Fit PCA Model on Data

Step 4: Access Principal Components and Explained Variance
Principal Components (Eigenvectors):
array([[ 0.70710678,  0.70710678],
       [-0.70710678,  0.70710678]])
Explained Variance for Each Principal Component:
array([8., 0.])

Step 5: Eigendecomposition of Covariance Matrix
Eigenvalues:
array([8., 0.])
Eigenvectors:
array([[ 0.70710678,  0.70710678],
       [-0.70710678,  0.70710678]])

Step 6: Transform Data using PCA (Projection)
Transformed Data (Projected onto Principal Components):
array([[-2.828427, -0.      ],
       [ 0.      ,  0.      ],
       [ 2.828427,  0.      ]])

Principal Component Analysis (PCA) stands as a swift and adaptable unsupervised technique for condensing the dimensionality of data. We caught a glimpse of its functionality in the earlier discussion on Scikit-Learn.

Example: Let’s focus on a two-dimensional dataset. For the purpose of illustration, let’s examine the subsequent set of 400 data points [VanderPlas, 2023]:

# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt

# Set custom style using mystyle.mplstyle
plt.style.use('../mystyle.mplstyle')

# Set random seed for reproducibility
rng = np.random.RandomState(1)

# Generate random data using dot product of random matrix and normal distribution
X = np.dot(rng.rand(2, 2), rng.randn(2, 400)).T

# Create a scatter plot
fig, ax = plt.subplots(figsize=(7, 7))
_ = ax.scatter(X[:, 0], X[:, 1], c='Aqua', edgecolors='DodgerBlue', s=30)

# Set plot properties such as aspect ratio, limits, and labels
_ = ax.set(aspect='equal', xlim=[-4, 4], ylim=[-2, 2], xlabel=r'$X_1$', ylabel=r'$X_2$')

# Ensure tight layout
plt.tight_layout()

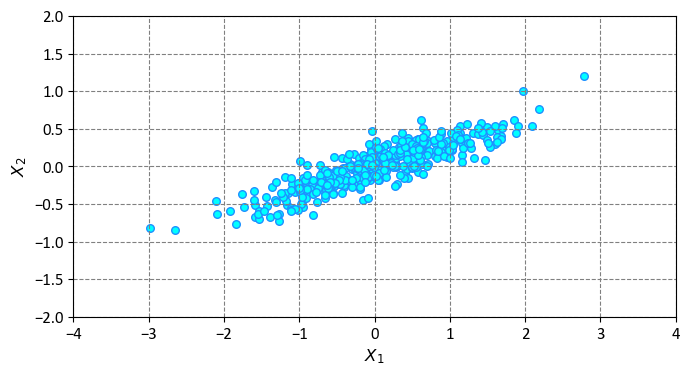
This code creates a synthetic dataset with two features (\(X_1\) and \(X_2\)) and 400 data points. The data points are generated by multiplying a random matrix with a normal distribution, which introduces some correlation between the features. The code then plots the data points on a scatter plot, where each point is colored in aqua and has a dodger blue edge. The plot also has equal aspect ratio, limits, and labels for the axes.

By visual inspection, it becomes evident that a nearly linear connection exists between the \(X_1\) and \(X_2\) variables in this dataset. However, the objective here differs slightly: instead of aiming to predict \(X_2\) values based on \(X_1\) values, the focus of unsupervised learning is to uncover the relationship between the \(X_1\) and \(X_2\) variables [VanderPlas, 2023].

Principal Component Analysis (PCA) serves as the tool to quantify this relationship. It achieves this by identifying the primary axes within the data and utilizing them to encapsulate the dataset’s characteristics [VanderPlas, 2023].

To carry out PCA using Scikit-Learn’s PCA estimator, follow these steps:

• Import the PCA class from the sklearn.decomposition module.

• Create an instance of the PCA class with the desired number of components. For example, pca = PCA(n_components=2) creates a PCA object that can transform the data into two dimensions.

• Fit the PCA object to the data using the fit method. For example, pca.fit(X) fits the PCA object to the data matrix X and computes the principal components and the explained variance.

• Transform the data into the new feature space using the transform method. For example, X_pca = pca.transform(X) transforms the data matrix X into the new matrix X_pca, where each row corresponds to a data point and each column corresponds to a principal component.

from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

# Define arrow plot settings
plt_setting = dict(head_width=0.1, head_length=0.2, linewidth=1.5, facecolor='black', edgecolor='black')

def plot_arrow(ax, start, end, **kwargs):
    # Function to plot an arrow on the given axis
    ax.arrow(start[0], start[1], end[0], end[1], **kwargs)

# Perform PCA with 2 components
pca = PCA(n_components=2)
pca.fit(X)

# Create a scatter plot
fig, ax = plt.subplots(figsize=(7, 7))
_ = ax.scatter(X[:, 0], X[:, 1], c='GreenYellow', edgecolors='Olive', s=30)
_ = ax.set(aspect='equal', xlim=[-4, 4], ylim=[-2, 2], xlabel=r'$X_1$', ylabel=r'$X_2$')

# Visualize the principal components using ax.arrow()
for length, vector in zip(pca.explained_variance_, pca.components_):
    v = vector * 3 * np.sqrt(length)  # Scale vector by a factor of 3 times the square root of the variance
    plot_arrow(ax, start=pca.mean_, end=v, **plt_setting)

plt.tight_layout()

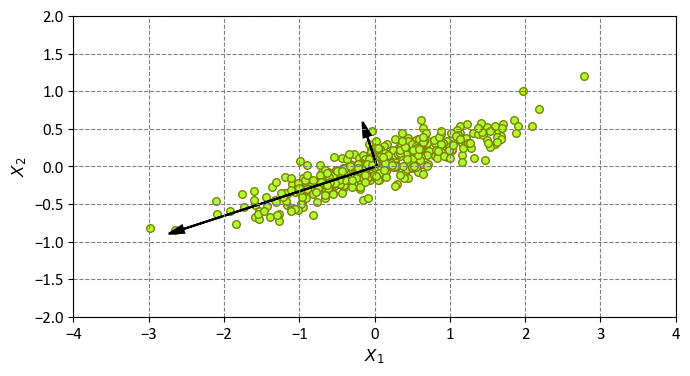
This code performs PCA on the data matrix X and plots the data points and the principal components on a scatter plot. The principal components are the new features that capture the most significant variations in the data. They are represented by the black arrows on the plot, which indicate the directions and lengths of the principal components. The directions are given by the eigenvectors of the covariance matrix, and the lengths are proportional to the square roots of the eigenvalues, which measure the amount of variance explained by each principal component.

These vectors embody the essence of the principal axes within the dataset. The length of each vector serves as a gauge for the axis’s significance in characterizing the data’s distribution—more precisely, it quantifies the variance of the data when projected onto that particular axis. The outcome of projecting each data point onto these principal axes gives birth to what we refer to as the “principal components” of the data [VanderPlas, 2023].

If we plot these principal components beside the original data, we see the plots shown here:

fig, ax = plt.subplots(1, 2, figsize=(9.5, 4.5))

# Plot original data and principal components
_ = ax[0].scatter(X[:, 0], X[:, 1], c='Aqua', edgecolors='DodgerBlue', s=30)
_ = ax[0].set(aspect='equal', xlim=[-4, 4], ylim=[-4, 4], xlabel=r'$X_1$', ylabel=r'$X_2$')
for length, vector in zip(pca.explained_variance_, pca.components_):
    v = vector * 3 * np.sqrt(length)
    plot_arrow(ax[0], start=pca.mean_, end=v, **plt_setting)

# Plot principal components
X_pca = pca.transform(X)
_ = ax[1].scatter(X_pca[:, 0], X_pca[:, 1], c='MistyRose', edgecolors='OrangeRed', s=30)
plot_arrow(ax[1], start=[0, 0], end=[0, 3], **plt_setting)
plot_arrow(ax[1], start=[0, 0], end=[3, 0], **plt_setting)
_ = ax[1].set(aspect='equal', xlabel='component 1', ylabel='component 2',
          title='principal components', xlim=(-4, 4), ylim=(-4, 4))

plt.tight_layout()

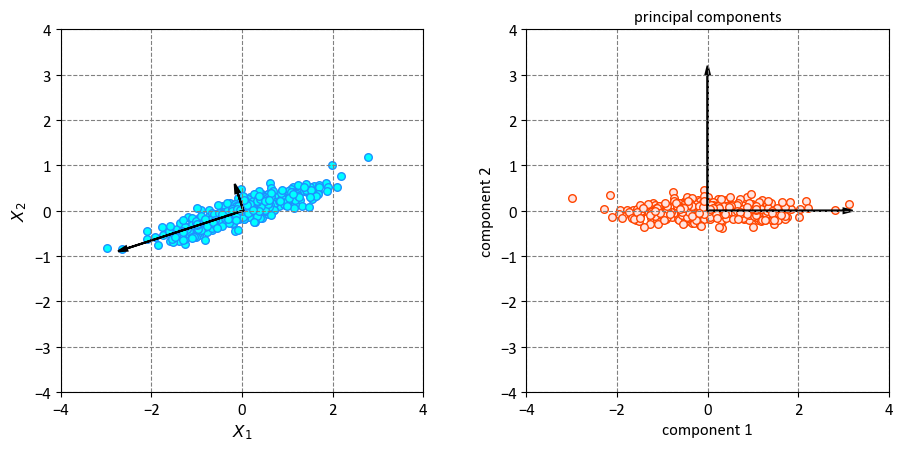
This code plots the original data and the principal components on two subplots. The first subplot shows the data points and the principal components as black arrows on the original feature space. The second subplot shows the data points and the principal components as black arrows on the new feature space. The principal components are the new features that capture the most significant variations in the data. They are represented by the black arrows on the plot, which indicate the directions and lengths of the principal components. The directions are given by the eigenvectors of the covariance matrix, and the lengths are proportional to the square roots of the eigenvalues, which measure the amount of variance explained by each principal component.

The process of transitioning from data axes to principal axes involves an affine transformation, which encompasses a combination of translation, rotation, and uniform scaling operations [VanderPlas, 2023].

Although this method for discovering principal components might initially appear as a mathematical concept, its implications extend far beyond theoretical curiosity. In fact, it plays a pivotal role in various applications within the domains of machine learning and data exploration [VanderPlas, 2023]. For example, PCA can be used to reduce the dimensionality of high-dimensional data, to visualize complex data structures, to remove noise from data, to extract features for classification or regression tasks, and to perform data compression or encryption.

11.2.3. PCA for Dimensionality Reduction

Utilizing PCA to reduce dimensionality means discarding one or more of the smallest principal components. This results in a lower-dimensional representation of the data that preserves the most important variations in the data.

Here’s an example of how PCA can be used for dimensionality reduction:

# Initialize PCA with the desired number of components (in this case, 1)
pca = PCA(n_components=1)

# Fit the PCA model to the data
pca.fit(X)

# Transform the original data using the trained PCA model
X_pca = pca.transform(X)

# Print the shape of the original and transformed data
print("Original shape:   ", X.shape)
print("Transformed shape:", X_pca.shape)

Original shape:    (400, 2)
Transformed shape: (400, 1)

The data after transformation now exists in a singular dimension. This means that each data point is represented by a single value, which is the projection of the original data point onto the first principal component. To grasp the implications of this reduction in dimensionality, we can reverse the transformation of this condensed data and generate a visualization by comparing it with the initial dataset. We can do this by using the inverse_transform method of the PCA object, which reconstructs the original data from the transformed data by adding back the discarded components. For example, X_new = pca.inverse_transform(X_pca) will create a new matrix X_new that has the same shape as the original matrix X, but with less variance.

X_new = pca.inverse_transform(X_pca)
fig, ax = plt.subplots(figsize = (7, 7))
_ = ax.scatter(X[:, 0], X[:, 1], c='Aqua', edgecolors='DodgerBlue', s=30)
_ = ax.scatter(X_new[:, 0], X_new[:, 1], c='OrangeRed', edgecolors='DarkRed', s=30)
_ = ax.set(aspect='equal', xlim=[-4, 4], ylim=[-2, 2], xlabel = r'$X_1$', ylabel = r'$X_2$')
plt.tight_layout()

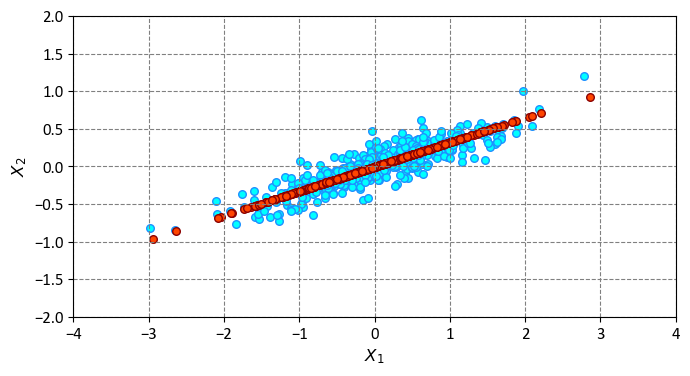
The blue dots represent the original dataset, while the red dots depict the reconstructed version from the transformed data. This clearly illustrates the essence of PCA-driven dimensionality reduction: it eliminates the data’s less significant principal axes, retaining solely the component(s) with the greatest variability. The proportion of variance that gets removed (related to the extent of dot dispersion around the line shown in this figure) serves as an approximate gauge of the extent of “information” discarded in this dimensionality reduction process.

In several aspects, this downsized dataset adequately captures the most vital connections among the points: even with a 50% reduction in data dimensionality, the fundamental relationships between data points are largely conserved. However, some information is inevitably lost in the process, as the red dots are not exactly the same as the blue dots. The difference between the original and the reconstructed data points is the projection error, which measures how well the principal components represent the data. The projection error is minimized when the principal components explain the most variance in the data.

11.2.3.1. Utilizing PCA for Visualization: Handwritten Digits

One of the applications of dimensionality reduction is to visualize high-dimensional data in a lower-dimensional space. This can help us explore the structure and patterns of the data, as well as identify outliers or anomalies. However, dimensionality reduction is not always straightforward or easy, especially when the data has a large number of dimensions.

Let’s examine the Optical Recognition of Handwritten Digits dataset provided by the sklearn library (This is only a subset of the original dataset with 5620 instances). This dataset contains 1797 images of handwritten digits, each with 64 pixels. Each pixel is a feature that represents the grayscale intensity of the image, ranging from 0 to 16. Therefore, each image is a data point with 64 dimensions. This dataset is a prime candidate for showcasing the power of PCA-based visualization [VanderPlas, 2023, scikit-learn Developers, 2023]. PCA can help us reduce the dimensionality of the images from 64 to 2, while preserving the most important variations in the data. This way, we can plot the images on a two-dimensional scatter plot and see how they are related to each other.

from sklearn.datasets import load_digits
digits = load_digits()
print(digits.DESCR)

import matplotlib.pyplot as plt

fig, axs = plt.subplots(nrows=10, ncols=10, figsize=(6, 6))
for idx, ax in enumerate(axs.ravel()):
    ax.imshow(digits.data[idx].reshape((8, 8)), cmap=plt.cm.binary)
    ax.axis("off")
_ = fig.suptitle("A selection from the 64-dimensional digits dataset", fontsize=16)
plt.tight_layout()

.. _digits_dataset:

Optical recognition of handwritten digits dataset
--------------------------------------------------

**Data Set Characteristics:**

    :Number of Instances: 1797
    :Number of Attributes: 64
    :Attribute Information: 8x8 image of integer pixels in the range 0..16.
    :Missing Attribute Values: None
    :Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)
    :Date: July; 1998

This is a copy of the test set of the UCI ML hand-written digits datasets
https://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits

The data set contains images of hand-written digits: 10 classes where
each class refers to a digit.

Preprocessing programs made available by NIST were used to extract
normalized bitmaps of handwritten digits from a preprinted form. From a
total of 43 people, 30 contributed to the training set and different 13
to the test set. 32x32 bitmaps are divided into nonoverlapping blocks of
4x4 and the number of on pixels are counted in each block. This generates
an input matrix of 8x8 where each element is an integer in the range
0..16. This reduces dimensionality and gives invariance to small
distortions.

For info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.
T. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.
L. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,
1994.

.. topic:: References

  - C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their
    Applications to Handwritten Digit Recognition, MSc Thesis, Institute of
    Graduate Studies in Science and Engineering, Bogazici University.
  - E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.
  - Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.
    Linear dimensionalityreduction using relevance weighted LDA. School of
    Electrical and Electronic Engineering Nanyang Technological University.
    2005.
  - Claudio Gentile. A New Approximate Maximal Margin Classification
    Algorithm. NIPS. 2000.

To develop a better understanding of the interconnections among these points, we can employ PCA to transform them into a more manageable number of dimensions, such as two:

from sklearn.decomposition import PCA
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

# Load the digits dataset
digits = load_digits()

# Apply PCA to project data to 2 dimensions
pca = PCA(n_components=2)  # project from 64 to 2 dimensions
projected = pca.fit_transform(digits.data)

# Print shapes before and after PCA
print("Original data shape:", digits.data.shape)
print("Projected data shape:", projected.shape)

# Create a scatter plot using Matplotlib
fig, ax = plt.subplots(1, 1, figsize=(9.5, 9.5))
scatter = ax.scatter(projected[:, 0], projected[:, 1],
                     c=digits.target, cmap='Spectral',
                     edgecolor='k', lw = 0.5,
                     alpha=0.7, s=40)

# Set labels and title
ax.set(xlabel='Component 1', ylabel='Component 2',
       title='PCA Projection of Handwritten Digits')

# Add legend inside on the top right
legend = ax.legend(*scatter.legend_elements(), title="Digits",
                   loc='upper right', fontsize = 12)

# Display the plot with tight layout
plt.tight_layout()

Original data shape: (1797, 64)
Projected data shape: (1797, 2)

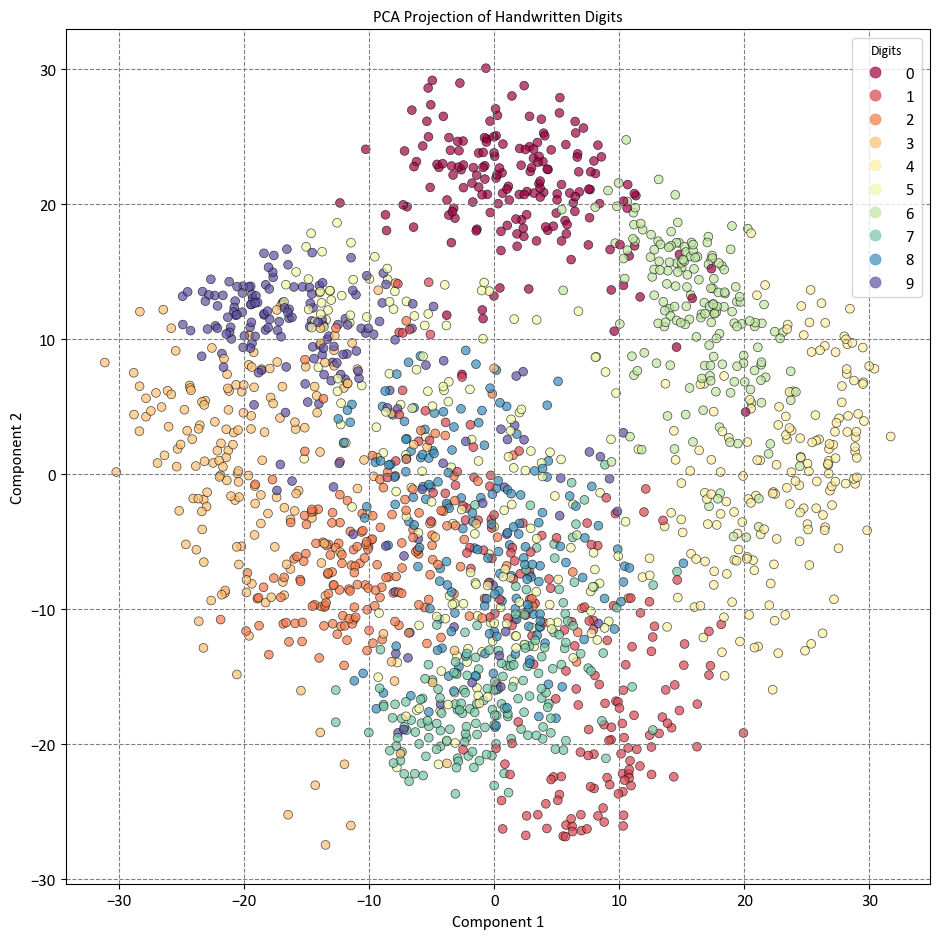
The complete dataset forms a cloud of points in a 64-dimensional space, while these specific points represent the projection of each data point along the directions characterized by the highest variance. Fundamentally, we’ve identified the optimal scaling and rotation within the 64-dimensional domain, enabling us to visualize the arrangement of the digits within two dimensions. Importantly, this process is unsupervised—meaning, it’s accomplished without using any label information [VanderPlas, 2023, scikit-learn Developers, 2023].

The code performs PCA on the digits dataset and plots the projected data on a two-dimensional scatter plot. The digits dataset contains 1797 images of handwritten digits, each with 64 pixels. Each pixel is a feature that represents the grayscale intensity of the image, ranging from 0 to 16.

print('Shape:', digits.data.shape)
print(digits.data.max(axis = 1))

Shape: (1797, 64)
[15. 16. 16. ... 16. 16. 16.]

Therefore, each image is a data point with 64 dimensions. PCA reduces the dimensionality of the images from 64 to 2, while preserving the most important variations in the data. The projected data is colored by the digit label, which ranges from 0 to 9. The plot shows how the different digits are clustered or separated in the new feature space. For example, the digits 0, 6, and 4 are well separated from the rest, while the digits 1 and 7 are more mixed. The plot also shows the component 1 and component 2 axes, which indicate the directions of the principal components. The principal components are the new features that capture the most significant variations in the data. They are represented by the black arrows on the plot, which indicate the directions and lengths of the principal components. The directions are given by the eigenvectors of the covariance matrix, and the lengths are proportional to the square roots of the eigenvalues, which measure the amount of variance explained by each principal component.